help links subscribe changes refresh edit

	SandBoxCombfunc
	↑

SandBoxCombfuncDiscussion

Edit detail for SandBoxCombfuncDiscussion revision 5 of 7

	1 2 3 4 5 6 7
Editor: Bill Page Time: 2017/04/07 21:38:49 GMT+0
Note: simplification of binomials

added:

From BillPage Fri Apr 7 21:38:48 +0000 2017
From: Bill Page
Date: Fri, 07 Apr 2017 21:38:48 +0000
Subject: simplification of binomials
Message-ID: <20170407213848+0000@axiom-wiki.newsynthesis.org>

The simplifications provided by Combfunc apply only to specific integer values of the 2nd argument of a single kernel. What you want to do usually involves combinations of more than one kernel.  For this you might expect something like 'simplify' or 'expand' to work but these commands are not aware of 'binomial'.  The next best thing might be to use some custom rules. E.g.
\begin{axiom}
BS := rule
  binomial(a,a-b) == binomial(a,b)
\end{axiom}
then we have
\begin{axiom}
Is(binomial(3,3-x),lhs BS)
binomial(3,x)-binomial(3,3-x)
BS( binomial(3,x)-binomial(3,3-x) )
\end{axiom}

This rule is already built-in
\begin{axiom}
BN := rule
  binomial(-n+k-1,k | even? k) == binomial(n,k)
  binomial(-n+k-1,k | odd? k) == -binomial(n,k)
binomial(-n+1,2)
binomial(-n+2,3)
\end{axiom}

Cross product. Note that because pattern matching is syntactic we need to take care about the lexical ordering of the variables.
\begin{axiom}
BX := rule
  binomial(k,n)*binomial(n,j) == binomial(k,j)*binomial(k-j,n-j)
  binomial(k,j)*binomial(n,k) == binomial(n,j)*binomial(n-j,k-j)
\end{axiom}

\begin{axiom}
ex1 := binomial(x+y,y)*binomial(y,y+z) 
ex2 := BX( binomial(x+y,y)*binomial(y,y+z) )
eval(ex1-ex2,[x=3,y=5,z=7])
\end{axiom}

Tests from GouldBk?.pdf --rrogers, Fri, 07 Apr 2017 16:22:25 +0000 reply

fricas

binomial(5,2)-binomial(5,5-2)

$\label{eq1}0$

(1)

Type: NonNegativeInteger?

fricas

binomial(a,b)-binomial(a,a-b)

$\label{eq2}{\hbox{\axiomType{BINOMIAL}\ } \left({a , \: b}\right)}-{\hbox{\axiomType{BINOMIAL}\ } \left({a , \:{- b + a}}\right)}$

(2)

Type: Expression(Integer)

Ah well no joy in Mudville I guess I need a special function of some sort, any comments?

simplification of binomials --Bill Page, Fri, 07 Apr 2017 21:38:48 +0000 reply

The simplifications provided by Combfunc apply only to specific integer values of the 2nd argument of a single kernel. What you want to do usually involves combinations of more than one kernel. For this you might expect something like simplify or expand to work but these commands are not aware of binomial. The next best thing might be to use some custom rules. E.g.

fricas

BS := rule
  binomial(a,a-b) == binomial(a,b)

$\label{eq1}{\hbox{\axiomType{BINOMIAL}\ } \left({a , \:{- b + a}}\right)}\mbox{\rm = =}{{{\tt'}binomial}\left({a , \: b}\right)}$

(1)

Type: RewriteRule?(Integer,Integer,Expression(Integer))

then we have

fricas

Is(binomial(3,3-x),lhs BS)

$\label{eq2}\left[{b = x}, \:{a = 3}\right]$

(2)

Type: List(Equation(Expression(Integer)))

fricas

binomial(3,x)-binomial(3,3-x)

$\label{eq3}{\hbox{\axiomType{BINOMIAL}\ } \left({3, \: x}\right)}-{\hbox{\axiomType{BINOMIAL}\ } \left({3, \:{- x + 3}}\right)}$

(3)

Type: Expression(Integer)

fricas

BS( binomial(3,x)-binomial(3,3-x) )

$\label{eq4}0$

(4)

Type: Expression(Integer)

This rule is already built-in

fricas

BN := rule
  binomial(-n+k-1,k | even? k) == binomial(n,k)
  binomial(-n+k-1,k | odd? k) == -binomial(n,k)

$\label{eq5}\begin{array}{@{}l} \displaystyle \left\{{{\hbox{\axiomType{BINOMIAL}\ } \left({{- n + k - 1}, \: k}\right)}\mbox{\rm = =}{{{\tt'}binomial}\left({n , \: k}\right)}}, \: \right. \ \ \displaystyle \left.{{\hbox{\axiomType{BINOMIAL}\ } \left({{- n + k - 1}, \: k}\right)}\mbox{\rm = =}-{{{\tt'}binomial}\left({n , \: k}\right)}}\right\}$

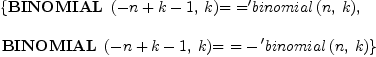(5)

Type: Ruleset(Integer,Integer,Expression(Integer))

fricas

binomial(-n+1,2)

$\label{eq6}{{{n}^{2}}- n}\over 2$

(6)

Type: Expression(Integer)

fricas

binomial(-n+2,3)

$\label{eq7}{-{{n}^{3}}+{3 \ {{n}^{2}}}-{2 \ n}}\over 6$

(7)

Type: Expression(Integer)

Cross product. Note that because pattern matching is syntactic we need to take care about the lexical ordering of the variables.

fricas

BX := rule
  binomial(k,n)*binomial(n,j) == binomial(k,j)*binomial(k-j,n-j)
  binomial(k,j)*binomial(n,k) == binomial(n,j)*binomial(n-j,k-j)

$\label{eq8}\begin{array}{@{}l} \displaystyle \left\{{{\%C \ {\hbox{\axiomType{BINOMIAL}\ } \left({k , \: n}\right)}\ {\hbox{\axiomType{BINOMIAL}\ } \left({n , \: j}\right)}}\mbox{\rm = =}{\%C \ {{{\tt'}binomial}\left({{k - j}, \:{n - j}}\right)}\ {{{\tt'}binomial}\left({k , \: j}\right)}}}, \right. \ \ \displaystyle \left.\: \right. \ \ \displaystyle \left.{{\%D \ {\hbox{\axiomType{BINOMIAL}\ } \left({k , \: j}\right)}\ {\hbox{\axiomType{BINOMIAL}\ } \left({n , \: k}\right)}}\mbox{\rm = =}{\%D \ {{{\tt'}binomial}\left({{n - j}, \:{k - j}}\right)}\ {{{\tt'}binomial}\left({n , \: j}\right)}}}\right\}$

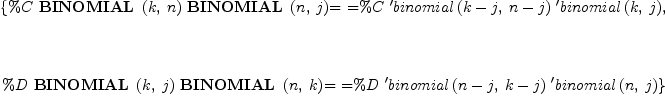(8)

Type: Ruleset(Integer,Integer,Expression(Integer))

fricas

ex1 := binomial(x+y,y)*binomial(y,y+z)

$\label{eq9}{\hbox{\axiomType{BINOMIAL}\ } \left({y , \:{z + y}}\right)}\ {\hbox{\axiomType{BINOMIAL}\ } \left({{y + x}, \: y}\right)}$

(9)

Type: Expression(Integer)

fricas

ex2 := BX( binomial(x+y,y)*binomial(y,y+z) )

$\label{eq10}{\hbox{\axiomType{BINOMIAL}\ } \left({{- z + x}, \: - z}\right)}\ {\hbox{\axiomType{BINOMIAL}\ } \left({{y + x}, \:{z + y}}\right)}$

(10)

Type: Expression(Integer)

fricas

eval(ex1-ex2,[x=3,y=5,z=7])

$\label{eq11}0$

(11)

Type: Expression(Integer)