|
|
|
last edited 12 years ago by test1 |
Edit detail for SandBoxCliffordAlgebra revision 8 of 9
| 1 2 3 4 5 6 7 8 9 | ||
|
Editor: test1
Time: 2013/03/18 00:58:21 GMT+0 |
||
| Note: | ||
changed: -dq := quadraticForm diagMat -CLDQ := CliffordAlgebra(3, Fraction(Integer), dq) CLDQ := CliffordAlgebra(3, Fraction(Integer), diagMat) changed: -where dq is the diagonal quadratic form in the basis of generators ei=e(i) corresponding to the diagonal quadratic form in the basis of generators ei=e(i) changed: -odq := quadraticForm offDiagMat -CLODQ := CliffordAlgebra(3, Fraction(Integer), odq) CLODQ := CliffordAlgebra(3, Fraction(Integer), offDiagMat) changed: -which is irritating, since the Clifford product is just 'unevaluated', hence the -basis elements are generated by Cliffrord products. We would like to see this more -explicit in the Grassmann basis, which we define as follows: -\begin{axiom} -f12: CLODQ := 1/2*( e(1)*e(2)-e(2)*e(1) ) -f13: CLODQ := 1/2*( e(1)*e(3)-e(3)*e(1) ) -f23: CLODQ := 1/2*( e(2)*e(3)-e(3)*e(2) ) -f123: CLODQ := 1/3*( f12*e(3)$CLODQ- f13*e(2)$CLODQ + f23*e(1)$CLODQ ) -- need this od $CLODQ -fbasis:List CLODQ :=[ 1, e(1), e(2), f12 , e(3), f13 , f23, f123 ] -\end{axiom} -and this is plainly wrong. Eg -\begin{equation} -f_{13} = \frac{1}{2}\ e_1 e_3 - \frac{1}{2} \ (e_3 \wedge e_1 + B(e_3,e_1)) -\end{equation} -and further simplification leads to -\begin{eqnarray} -f_{13} &=& \frac{1}{2} \ e_1 e_3 + \frac{1}{2} \ ( e_1 \wedge e_3 - B(e_1,e_3)) \\ -&=& e_1 e_3 - \frac{1}{2} \ B(e_1,e_3) -\end{eqnarray} -and all these off diagonal contraction -terms are missing in the basis. Hence the $\text{AXIOM}^{TM}$ CliffordAlgebra domain works only in the basis of generators -which diagonalized the quadratic form! - -Actually this calls for a new domain CliffordAlgebra which does it right ;-). - Note: Before Martin Baker fixed CliffordAlgebra the results with off diagonal form were wrong.
We want to test some properties of the CliffordAlgebra? domain implemented in AXIOM(TM)
fricas
diagMat:=matrix[[1,0, 0], [0, 1, 0], [0, 0, 1]]
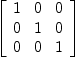 | (1) |
Type: Matrix(NonNegativeInteger?)
fricas
CLDQ := CliffordAlgebra(3,Fraction(Integer), diagMat)
| (2) |
Type: Type
CLDQ contains now the Clifford algebra constructor for the Clifford algebra CL(R^3,Q) corresponding to the diagonal quadratic form in the basis of generators ei=e(i)
fricas
basGen: List CLDQ :=[1,e(1), e(2), e(1)*e(2), e(3), e(1)*e(3), e(2)*e(3), e(1)*e(2)*e(3)]
| (3) |
And we can now compute within this basis
fricas
elem1: CLDQ :=2*e(1)+e(2)
| (4) |
fricas
elem2: CLDQ :=1/2+e(2)+3*e(1)*e(3)
| (5) |
fricas
elem1*elem2
| (6) |
which is fine.
Lets now see what happens if we change the basis. We define new generators
fricas
f1:CLDQ := e(1)-e(2)
| (7) |
fricas
f2:CLDQ := e(2)-e(3)
| (8) |
fricas
f3:CLDQ := e(1)+e(2)+e(3)
| (9) |
fricas
lstFGen: List CLDQ := [f1,f2, f3]
| (10) |
and check what the new defining relations are
fricas
matrix [[y*x for x in lstFGen] for y in lstFGen]
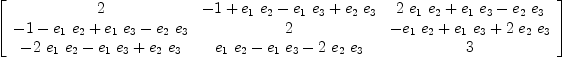 | (11) |
However, let us do the same calculations with another, symmetric but not diagonal quadratic form
fricas
offDiagMat:=matrix[[0,0, 1], [0, 1, 0], [1, 0, 0]]
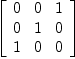 | (12) |
Type: Matrix(NonNegativeInteger?)
fricas
CLODQ := CliffordAlgebra(3,Fraction(Integer), offDiagMat)
| (13) |
Type: Type
fricas
basGenO: List CLODQ :=[1,e(1), e(2), e(1)*e(2), e(3), e(1)*e(3), e(2)*e(3), e(1)*e(2)*e(3)]
| (14) |
fricas
basO: List CLODQ :=[e(1),e(2), e(3)]
| (15) |
and let us check the multiplication table on the basis and in general:
fricas
matrix [[y*x for x in basO] for y in basO]
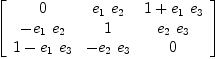 | (16) |
fricas
matrix [[y*x for x in basGenO] for y in basGenO]
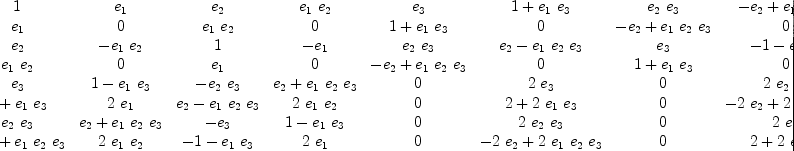 | (17) |
Note: Before Martin Baker fixed CliffordAlgebra? the results with off diagonal form were wrong.