|
|
|
last edited 14 years ago by Bill Page |
Edit detail for SandBoxCartesianTensor revision 5 of 5
| 1 2 3 4 5 | ||
|
Editor: Bill Page
Time: 2011/04/27 23:37:42 GMT-7 |
||
| Note: fast n-ary contraction | ||
Try to make it a little faster.
fricas
(1) -> <spad>
fricas
)abbrev domain CARTEN CartesianTensor ++ Author: Stephen M. Watt ++ Date Created: December 1986 ++ Date Last Updated: May 15,1991 ++ Basic Operations: ++ Related Domains: ++ Also See: ++ AMS Classifications: ++ Keywords: tensor, graded algebra ++ Examples: ++ References: ++ Description: ++ CartesianTensor(minix, dim, R) provides Cartesian tensors with ++ components belonging to a commutative ring R. These tensors ++ can have any number of indices. Each index takes values from ++ \spad{minix} to \spad{minix + dim - 1}.
CartesianTensor(minix,dim, R): Exports == Implementation where NNI ==> NonNegativeInteger I ==> Integer DP ==> DirectProduct SM ==> SquareMatrix
minix: Integer dim: NNI R: CommutativeRing
Exports ==> Join(GradedAlgebra(R,NNI), GradedModule(I, NNI)) with
coerce: DP(dim,R) -> % ++ coerce(v) views a vector as a rank 1 tensor. coerce: SM(dim, R) -> % ++ coerce(m) views a matrix as a rank 2 tensor.
coerce: List R -> % ++ coerce([r_1,..., r_dim]) allows tensors to be constructed ++ using lists.
coerce: List % -> % ++ coerce([t_1,..., t_dim]) allows tensors to be constructed ++ using lists.
rank: % -> NNI ++ rank(t) returns the tensorial rank of t (that is,the ++ number of indices). This is the same as the graded module ++ degree.
elt: (%) -> R ++ elt(t) gives the component of a rank 0 tensor. elt: (%,I) -> R ++ elt(t, i) gives a component of a rank 1 tensor. elt: (%, I, I) -> R ++ elt(t, i, j) gives a component of a rank 2 tensor. elt: (%, I, I, I) -> R ++ elt(t, i, j, k) gives a component of a rank 3 tensor. elt: (%, I, I, I, I) -> R ++ elt(t, i, j, k, l) gives a component of a rank 4 tensor.
elt: (%,List I) -> R ++ elt(t, [i1, ..., iN]) gives a component of a rank \spad{N} tensor.
-- This specializes the documentation from GradedAlgebra. product: (%,%) -> % ++ product(s, t) is the outer product of the tensors s and t. ++ For example, if \spad{r = product(s, t)} for rank 2 tensors s and t, ++ then \spad{r} is a rank 4 tensor given by ++ \spad{r(i, j, k, l) = s(i, j)*t(k, l)}.
"*": (%,%) -> % ++ s*t is the inner product of the tensors s and t which contracts ++ the last index of s with the first index of t, i.e. ++ \spad{t*s = contract(t, rank t, s, 1)} ++ \spad{t*s = sum(k=1..N, t[i1, .., iN, k]*s[k, j1, .., jM])} ++ This is compatible with the use of \spad{M*v} to denote ++ the matrix-vector inner product.
contract: (%,Integer, %, Integer) -> % ++ contract(t, i, s, j) is the inner product of tenors s and t ++ which sums along the \spad{i}-th index of ++ t and the \spad{j}-th index of s. ++ For example, if \spad{r = contract(s, 2, t, 1)} for ++ rank 3 tensors \spad{s} and \spad{t}, then \spad{r} is ++ the rank 4 \spad{(= 3 + 3 - 2)} tensor given by ++ \spad{r(i, j, k, l) = sum(h=1..dim, s(i, h, j)*t(h, k, l))}.
contract: (Integer,%, Integer, %, Integer) -> % ++ contract(n, t, i, s, j) is n-fold inner product of tenors ++ s and t which sums along n indices of t starting at ++ \spad{i} and n indices of s starting at \spad{j}. ++ For example, if \spad{r = contract(2, s, 2, t, 1)} for ++ rank 3 tensors \spad{s} and \spad{t}, then \spad{r} is ++ the rank 2 \spad{(= 3 + 3 - 2*2)} tensor given by ++ \spad{r(i, l) = sum(h2=1..dim, sum(h1=1..dim, s(i, h1, h2)*t(h1, h2, l)))}.
contract: (%,Integer, Integer) -> % ++ contract(t, i, j) is the contraction of tensor t which ++ sums along the \spad{i}-th and \spad{j}-th indices. ++ For example, if ++ \spad{r = contract(t, 1, 3)} for a rank 4 tensor t, then ++ \spad{r} is the rank 2 \spad{(= 4 - 2)} tensor given by ++ \spad{r(i, j) = sum(h=1..dim, t(h, i, h, j))}.
transpose: % -> % ++ transpose(t) exchanges the first and last indices of t. ++ For example,if \spad{r = transpose(t)} for a rank 4 tensor t, then ++ \spad{r} is the rank 4 tensor given by ++ \spad{r(i, j, k, l) = t(l, j, k, i)}.
transpose: (%,Integer, Integer) -> % ++ transpose(t, i, j) exchanges the \spad{i}-th and \spad{j}-th indices of t. ++ For example, if \spad{r = transpose(t, 2, 3)} for a rank 4 tensor t, then ++ \spad{r} is the rank 4 tensor given by ++ \spad{r(i, j, k, l) = t(i, k, j, l)}.
reindex: (%,List Integer) -> % ++ reindex(t, [i1, ..., idim]) permutes the indices of t. ++ For example, if \spad{r = reindex(t, [4, 1, 2, 3])} ++ for a rank 4 tensor t, ++ then \spad{r} is the rank for tensor given by ++ \spad{r(i, j, k, l) = t(l, i, j, k)}.
kroneckerDelta: () -> % ++ kroneckerDelta() is the rank 2 tensor defined by ++ \spad{kroneckerDelta()(i,j)} ++ \spad{= 1 if i = j} ++ \spad{= 0 if i \~= j}
leviCivitaSymbol: () -> % ++ leviCivitaSymbol() is the rank \spad{dim} tensor defined by ++ \spad{leviCivitaSymbol()(i1,...idim) = +1/0/-1} ++ if \spad{i1, ..., idim} is an even/is nota /is an odd permutation ++ of \spad{minix, ..., minix+dim-1}. ravel: % -> List R ++ ravel(t) produces a list of components from a tensor such that ++ \spad{unravel(ravel(t)) = t}.
unravel: List R -> % ++ unravel(t) produces a tensor from a list of ++ components such that ++ \spad{unravel(ravel(t)) = t}.
sample: () -> % ++ sample() returns an object of type %.
Implementation ==> add
PERM ==> Vector Integer -- 1-based entries from 1..n INDEX ==> Vector Integer -- 1-based entries from minix..minix+dim-1
-- Use row-major order: -- x[h,i, j] <-> x[(h-minix)*dim^2+(i-minix)*dim+(j-minix)]
Rep := PrimitiveArray(R) --get ==> elt$Rep --set_! ==> setelt$Rep get(x:Rep,i:Integer):R == QAREF1(x pretend SExpression, i)$Lisp set_!(x:Rep, i:Integer, s:R):R == QSETAREF1(x pretend SExpression, i, s)$Lisp
n: Integer r,s: R x, y, z: %
---- Local stuff dim2: NNI := dim^2 dim3: NNI := dim^3 dim4: NNI := dim^4
sample()==kroneckerDelta()$% int2index(n: Integer,indv: INDEX): INDEX == n < 0 => error "Index error (too small)" rnk := #indv for i in 1..rnk repeat qr := divide(n, dim) n := qr.quotient indv.((rnk-i+1) pretend NNI) := qr.remainder + minix n ~= 0 => error "Index error (too big)" indv
index2int(indv: INDEX): Integer == n: I := 0 for i in 1..#indv repeat ix := indv.i - minix ix<0 or ix>dim-1 => error "Index error (out of range)" n := dim*n + ix n
lengthRankOrElse(v: Integer): NNI == v = 1 => 0 v = dim => 1 v = dim2 => 2 v = dim3 => 3 v = dim4 => 4 rx := 0 while v ~= 0 repeat qr := divide(v,dim) v := qr.quotient if v ~= 0 then qr.remainder ~= 0 => error "Rank is not a whole number" rx := rx + 1 rx
-- l must be a list of the numbers 1..#l mkPerm(n: NNI,l: List Integer): PERM == #l ~= n => error "The list is not a permutation." p: PERM := new(n, 0) seen: Vector Boolean := new(n, false) for i in 1..n for e in l repeat e < 1 or e > n => error "The list is not a permutation." p.i := e seen.e := true for e in 1..n repeat not seen.e => error "The list is not a permutation." p
-- permute s according to p into result t. permute_!(t: INDEX,s: INDEX, p: PERM): INDEX == for i in 1..#p repeat t.i := s.(p.i) t
-- permsign!(v) = 1,0, or -1 according as -- v is an even, is not, or is an odd permutation of minix..minix+#v-1. permsign_!(v: INDEX): Integer == -- sum minix..minix+#v-1. maxix := minix+#v-1 psum := (((maxix+1)*maxix - minix*(minix-1)) exquo 2)::Integer -- +/v ~= psum => 0 n := 0 for i in 1..#v repeat n := n + v.i n ~= psum => 0 -- Bubble sort! This is pretty grotesque. totTrans: Integer := 0 nTrans: Integer := 1 while nTrans ~= 0 repeat nTrans := 0 for i in 1..#v-1 for j in 2..#v repeat if v.i > v.j then nTrans := nTrans + 1 e := v.i; v.i := v.j; v.j := e totTrans := totTrans + nTrans for i in 1..dim repeat if v.i ~= minix+i-1 then return 0 odd? totTrans => -1 1
---- Exported functions ravel x == [get(x,i) for i in 0..#x-1]
unravel l == -- lengthRankOrElse #l gives sytnax error nz: NNI := # l lengthRankOrElse nz z := new(nz,0) for i in 0..nz-1 for r in l repeat set_!(z, i, r) z
kroneckerDelta() == z := new(dim2,0) for i in 1..dim for zi in 0.. by (dim+1) repeat set_!(z, zi, 1) z leviCivitaSymbol() == nz := dim^dim z := new(nz, 0) indv: INDEX := new(dim, 0) for i in 0..nz-1 repeat set_!(z, i, permsign_!(int2index(i, indv))::R) z
-- from GradedModule degree x == rank x
rank x == n := #x lengthRankOrElse n
elt(x) == #x ~= 1 => error "Index error (the rank is not 0)" get(x,0) elt(x, i: I) == #x ~= dim => error "Index error (the rank is not 1)" get(x, (i-minix)) elt(x, i: I, j: I) == #x ~= dim2 => error "Index error (the rank is not 2)" get(x, (dim*(i-minix) + (j-minix))) elt(x, i: I, j: I, k: I) == #x ~= dim3 => error "Index error (the rank is not 3)" get(x, (dim2*(i-minix) + dim*(j-minix) + (k-minix))) elt(x, i: I, j: I, k: I, l: I) == #x ~= dim4 => error "Index error (the rank is not 4)" get(x, (dim3*(i-minix) + dim2*(j-minix) + dim*(k-minix) + (l-minix)))
elt(x,i: List I) == #i ~= rank x => error "Index error (wrong rank)" n: I := 0 for ii in i repeat ix := ii - minix ix<0 or ix>dim-1 => error "Index error (out of range)" n := dim*n + ix get(x, n)
coerce(lr: List R): % == #lr ~= dim => error "Incorrect number of components" z := new(dim,0) for r in lr for i in 0..dim-1 repeat set_!(z, i, r) z coerce(lx: List %): % == #lx ~= dim => error "Incorrect number of slices" rx := rank first lx for x in lx repeat rank x ~= rx => error "Inhomogeneous slice ranks" nx := # first lx z := new(dim * nx, 0) for x in lx for offz in 0.. by nx repeat for i in 0..nx-1 repeat set_!(z, offz + i, get(x, i)) z
retractIfCan(x:%):Union(R,"failed") == zero? rank(x) => x() "failed" Outf ==> OutputForm
mkOutf(x:%,i0:I, rnk:NNI): Outf == odd? rnk => rnk1 := (rnk-1) pretend NNI nskip := dim^rnk1 [mkOutf(x, i0+nskip*i, rnk1) for i in 0..dim-1]::Outf rnk = 0 => get(x, i0)::Outf rnk1 := (rnk-2) pretend NNI nskip := dim^rnk1 matrix [[mkOutf(x, i0+nskip*(dim*i + j), rnk1) for j in 0..dim-1] for i in 0..dim-1] coerce(x): Outf == mkOutf(x, 0, rank x)
0 == 0$R::Rep 1 == 1$R::Rep
--coerce(n: I): % == new(1,n::R) coerce(r: R): % == new(1, r)
coerce(v: DP(dim,R)): % == z := new(dim, 0) for i in 0..dim-1 for j in minIndex v .. maxIndex v repeat set_!(z, i, v.j) z coerce(m: SM(dim, R)): % == z := new(dim^2, 0) offz := 0 for i in 0..dim-1 repeat for j in 0..dim-1 repeat set_!(z, offz + j, m(i+1, j+1)) offz := offz + dim z
x = y == #x ~= #y => false for i in 0..#x-1 repeat if get(x,i) ~= get(y, i) then return false true x + y == #x ~= #y => error "Rank mismatch" -- z := [xi + yi for xi in x for yi in y] z := new(#x, 0) for i in 0..#x-1 repeat set_!(z, i, get(x, i) + get(y, i)) z x - y == #x ~= #y => error "Rank mismatch" -- [xi - yi for xi in x for yi in y] z := new(#x, 0) for i in 0..#x-1 repeat set_!(z, i, get(x, i) - get(y, i)) z - x == -- [-xi for xi in x] z := new(#x, 0) for i in 0..#x-1 repeat set_!(z, i, -get(x, i)) z n * x == -- [n * xi for xi in x] z := new(#x, 0) for i in 0..#x-1 repeat set_!(z, i, n * get(x, i)) z x * n == -- [n * xi for xi in x] z := new(#x, 0) for i in 0..#x-1 repeat set_!(z, i, n* get(x, i)) -- Commutative!! z r * x == -- [r * xi for xi in x] z := new(#x, 0) for i in 0..#x-1 repeat set_!(z, i, r * get(x, i)) z x * r == -- [xi*r for xi in x] z := new(#x, 0) for i in 0..#x-1 repeat set_!(z, i, r* get(x, i)) -- Commutative!! z product(x, y) == nx := #x; ny := #y z := new(nx * ny, 0) for i in 0..nx-1 for ioff in 0.. by ny repeat xi := get(x, i) if not zero? xi then for j in 0..ny-1 repeat set_!(z, ioff + j, xi * get(y, j)) z x * y == rx := rank x ry := rank y rx = 0 => get(x, 0) * y ry = 0 => x * get(y, 0) contract(x, rx, y, 1)
contract(x,i, j) == rx := rank x i < 1 or i > rx or j < 1 or j > rx or i = j => error "Improper index for contraction" if i > j then (i, j) := (j, i)
rl:= (rx- j) pretend NNI; nl:= dim^rl; zol:= 1; xol:= zol rm:= (j-i-1) pretend NNI; nm:= dim^rm; zom:= nl; xom:= zom*dim rh:= (i - 1) pretend NNI; nh:= dim^rh; zoh:= nl*nm xoh:= zoh*dim^2 xok := nl*(1 + nm*dim) z := new(nl*nm*nh,0) for h in 1..nh _ for xh in 0.. by xoh for zh in 0.. by zoh repeat for m in 1..nm _ for xm in xh.. by xom for zm in zh.. by zom repeat for l in 1..nl _ for xl in xm.. by xol for zl in zm.. by zol repeat --set_!(z, zl, 0) zz:R:=0 for k in 1..dim for xk in xl.. by xok repeat --set_!(z, zl, get(z, zl) + get(x, xk)) zz := zz + get(x, xk) set_!(z, zl, zz) z
contract(x,i, y, j) == contract(1, x, i, y, j)
contract(n,x, i, y, j) == rx := rank x ry := rank y
i < 1 or i+n-1 > rx or j < 1 or j+n-1 > ry => error "Improper index for contraction"
-- width of trace nw:=dim^(n pretend NNI) -- rank of lower (right) part of y rly:= (ry-n-j+1) pretend NNI nly:= dim^rly -- spacing of lower y oly:= 1 zoly:= 1 -- rank of higher (left) part of y rhy:= (j-1) pretend NNI nhy:= dim^rhy -- spacing of higher y ohy:= nly*nw zohy:= zoly*nly -- rank of lower (right) part of x rlx:= (rx-n-i+1) pretend NNI nlx:= dim^rlx -- spacing of lower x olx:= 1 zolx:= zohy*nhy -- rank of higher (left) part of x rhx:= (i-1) pretend NNI nhx:= dim^rhx -- spacing of higher x ohx:= nlx*nw zohx:= zolx*nlx
-- result z := new(nlx*nhx*nly*nhy,0)
-- higher x index for dxh in 1..nhx _ for xh in 0.. by ohx for zhx in 0.. by zohx repeat -- lower x index for dxl in 1..nlx _ for xl in xh.. by olx for zlx in zhx.. by zolx repeat -- higher y index for dyh in 1..nhy _ for yh in 0.. by ohy for zhy in zlx.. by zohy repeat -- lower y index for dyl in 1..nly _ for yl in yh.. by oly for zly in zhy.. by zoly repeat --trace r:R:=get(z,zly) for nk in 1..nw _ for xk in xl.. by nlx for yk in yl.. by nly repeat r:=r+get(x, xk)*get(y, yk) set_!(z, zly, r) z
transpose x == transpose(x,1, rank x) transpose(x, i, j) == rx := rank x i < 1 or i > rx or j < 1 or j > rx or i = j => error "Improper indicies for transposition" if i > j then (i, j) := (j, i)
rl:= (rx- j) pretend NNI; nl:= dim^rl; zol:= 1; zoi := zol*nl rm:= (j-i-1) pretend NNI; nm:= dim^rm; zom:= nl*dim; zoj := zom*nm rh:= (i - 1) pretend NNI; nh:= dim^rh; zoh:= nl*nm*dim^2 z := new(#x,0) for h in 1..nh for zh in 0.. by zoh repeat _ for m in 1..nm for zm in zh.. by zom repeat _ for l in 1..nl for zl in zm.. by zol repeat _ for p in 1..dim _ for zp in zl.. by zoi for xp in zl.. by zoj repeat for q in 1..dim _ for zq in zp.. by zoj for xq in xp.. by zoi repeat set_!(z, zq, get(x, xq)) z
reindex(x,l) == nx := #x z: % := new(nx, 0)
rx := rank x p := mkPerm(rx,l) xiv: INDEX := new(rx, 0) ziv: INDEX := new(rx, 0)
-- Use permutation for i in 0..#x-1 repeat pi := index2int(permute_!(ziv,int2index(i, xiv), p)) set_!(z, pi, get(x, i)) z</spad>
fricas
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/6706617537521748663-25px001.spad
using old system compiler.
CARTEN abbreviates domain CartesianTensor
------------------------------------------------------------------------
initializing NRLIB CARTEN for CartesianTensor
compiling into NRLIB CARTEN
processing macro definition PERM ==> Vector Integer
processing macro definition INDEX ==> Vector Integer
compiling local get : (Rep,
compiling local set_! : (Rep,
compiling exported sample : () -> %
Time: 0 SEC.
compiling local int2index : (Integer,
compiling local index2int : Vector Integer -> Integer
Time: 0 SEC.
compiling local lengthRankOrElse : Integer -> NonNegativeInteger
Time: 0 SEC.
compiling local mkPerm : (NonNegativeInteger,
compiling local permute_! : (Vector Integer,
compiling local permsign_! : Vector Integer -> Integer
Time: 0.01 SEC.
compiling exported ravel : % -> List R
Time: 0 SEC.
compiling exported unravel : List R -> %
Time: 0 SEC.
compiling exported kroneckerDelta : () -> %
Time: 0 SEC.
compiling exported leviCivitaSymbol : () -> %
Time: 0 SEC.
compiling exported degree : % -> NonNegativeInteger
Time: 0 SEC.
compiling exported rank : % -> NonNegativeInteger
Time: 0 SEC.
compiling exported elt : % -> R
Time: 0 SEC.
compiling exported elt : (%,
compiling exported elt : (%,
compiling exported elt : (%,
compiling exported elt : (%,
compiling exported elt : (%,
compiling exported coerce : List R -> %
Time: 0 SEC.
compiling exported coerce : List % -> %
Time: 0 SEC.
compiling exported retractIfCan : % -> Union(R,
processing macro definition Outf ==> OutputForm
compiling local mkOutf : (%,
compiling exported coerce : % -> OutputForm
Time: 0 SEC.
compiling exported Zero : () -> %
Time: 0 SEC.
compiling exported One : () -> %
Time: 0 SEC.
compiling exported coerce : R -> %
CARTEN;coerce;R%;29 is replaced by MAKEARR11r
Time: 0 SEC.
compiling exported coerce : DirectProduct(dim,
compiling exported coerce : SquareMatrix(dim,
compiling exported = : (%,
compiling exported + : (%,
compiling exported - : (%,
compiling exported - : % -> %
Time: 0 SEC.
compiling exported * : (Integer,
compiling exported * : (%,
compiling exported * : (R,
compiling exported * : (%,
compiling exported product : (%,
compiling exported * : (%,
compiling exported contract : (%,
compiling exported contract : (%,
compiling exported contract : (Integer,
compiling exported transpose : % -> %
Time: 0 SEC.
compiling exported transpose : (%,
compiling exported reindex : (%,
(time taken in buildFunctor: 667)
;;; *** |CartesianTensor| REDEFINED
;;; *** |CartesianTensor| REDEFINED
Time: 0 SEC.
Warnings:
[1] index2int: n has no value
[2] permsign_!: nTrans has no value
[3] elt: n has no value
Cumulative Statistics for Constructor CartesianTensor
Time: 0.16 seconds
finalizing NRLIB CARTEN
Processing CartesianTensor for Browser database:
--------constructor---------
--------(coerce (% (DirectProduct dim R)))---------
--------(coerce (% (SquareMatrix dim R)))---------
--------(coerce (% (List R)))---------
--------(coerce (% (List %)))---------
--------(rank ((NonNegativeInteger) %))---------
--------(elt (R %))---------
--------(elt (R % (Integer)))---------
--------(elt (R % (Integer) (Integer)))---------
--------(elt (R % (Integer) (Integer) (Integer)))---------
--------(elt (R % (Integer) (Integer) (Integer) (Integer)))---------
--------(elt (R % (List (Integer))))---------
--------(product (% % %))---------
--------(* (% % %))---------
--------(contract (% % (Integer) % (Integer)))---------
--------(contract (% (Integer) % (Integer) % (Integer)))---------
--------(contract (% % (Integer) (Integer)))---------
--------(transpose (% %))---------
--------(transpose (% % (Integer) (Integer)))---------
--------(reindex (% % (List (Integer))))---------
--------(kroneckerDelta (%))---------
--------(leviCivitaSymbol (%))---------
--------(ravel ((List R) %))---------
--------(unravel (% (List R)))---------
--------(sample (%))---------
; compiling file "/var/aw/var/LatexWiki/CARTEN.NRLIB/CARTEN.lsp" (written 13 NOV 2025 07:27:55 PM):
; wrote /var/aw/var/LatexWiki/CARTEN.NRLIB/CARTEN.fasl
; compilation finished in 0:00:00.344
------------------------------------------------------------------------
CartesianTensor is now explicitly exposed in frame initial
CartesianTensor will be automatically loaded when needed from
/var/aw/var/LatexWiki/CARTEN.NRLIB/CARTENfricas
X:=unravel([script(x,[[i]]) for i in 0..2^2-1])$CartesianTensor(1, 2, EXPR INT)
| (1) |
fricas
Y:=unravel([script(y,[[i]]) for i in 0..2^2-1])$CartesianTensor(1, 2, EXPR INT)
| (2) |
fricas
XY:=contract(contract(X,1, Y, 1), 1, 2)
| (3) |
fricas
test(XY=contract(2,X, 1, Y, 1))
| (4) |
Type: Boolean
fricas
XY:=contract(X,2, Y, 1)
| (5) |
fricas
test(XY=contract(1,X, 2, Y, 1))
| (6) |
Type: Boolean
fricas
X:=unravel([script(x,[[i]]) for i in 0..2^3-1])$CartesianTensor(1, 2, EXPR INT)
 | (7) |
fricas
Y:=unravel([script(y,[[i]]) for i in 0..2^3-1])$CartesianTensor(1, 2, EXPR INT)
 | (8) |
fricas
XY:=contract(contract(contract(X,1, Y, 1), 1, 3), 1, 2)
| (9) |
fricas
test(XY=contract(3,X, 1, Y, 1))
| (10) |
Type: Boolean
fricas
test(product(X,Y)=contract(0, X, 1, Y, 1))
| (11) |
Type: Boolean
fricas
test(XY=contract(contract(contract(product(X,Y), 1, 4), 1, 3), 1, 2))
| (12) |
Type: Boolean
fricas
X:=unravel([script(x,[[i]]) for i in 0..2^4-1])$CartesianTensor(1, 2, EXPR INT)
 | (13) |
fricas
Y:=unravel([script(y,[[i]]) for i in 0..2^4-1])$CartesianTensor(1, 2, EXPR INT)
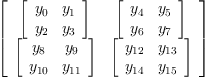 | (14) |
fricas
XY:=contract(contract(contract(contract(X,1, Y, 1), 1, 4), 1, 3), 1, 2)
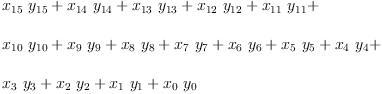 | (15) |
fricas
test(XY=contract(4,X, 1, Y, 1))
| (16) |
Type: Boolean
fricas
XY:=contract(contract(X,3, Y, 1), 3, 4)
 | (17) |
fricas
test(product(X,Y)=contract(0, X, 1, Y, 1))
| (18) |
Type: Boolean
fricas
test(XY=contract(contract(product(X,Y), 3, 5), 3, 4))
| (19) |
Type: Boolean
fricas
test(XY=contract(2,X, 3, Y, 1))
| (20) |
Type: Boolean