Non-degeneracy of the pairing (snake relation)
or equivalently
Ref:
We use the Axiom LinearOperator library
fricas
(1) -> )library CARTEN MONAL PROP LOP
CartesianTensor is now explicitly exposed in frame initial
CartesianTensor will be automatically loaded when needed from
/var/aw/var/LatexWiki/CARTEN.NRLIB/CARTEN
Monoidal is now explicitly exposed in frame initial
Monoidal will be automatically loaded when needed from
/var/aw/var/LatexWiki/MONAL.NRLIB/MONAL
Prop is now explicitly exposed in frame initial
Prop will be automatically loaded when needed from
/var/aw/var/LatexWiki/PROP.NRLIB/PROP
LinearOperator is now explicitly exposed in frame initial
LinearOperator will be automatically loaded when needed from
/var/aw/var/LatexWiki/LOP.NRLIB/LOP
and some convenient notation
fricas
macro Σ(x,i,n)==reduce(+,[x for i in n])
Type: Void
fricas
macro Ξ(f,i,n)==[f for i in n]
Type: Void
fricas
macro sb == subscript
Type: Void
fricas
macro sp == superscript
Type: Void
Let 𝐋 be the domain of 2-dimensional linear operators
fricas
dim:=2
fricas
macro ℒ == List
Type: Void
fricas
macro ℚ == Expression Integer
Type: Void
fricas
𝐋 := LinearOperator(OVAR ['1,'2], ℚ)
Type: Type
fricas
𝐞:ℒ 𝐋 := basisOut()
fricas
𝐝:ℒ 𝐋 := basisIn()
fricas
I:𝐋:=[1] -- identity for composition
fricas
X:𝐋:=[2,1] -- twist
Pairing
A scalar product (pairing) is represented by
fricas
U:=Σ(Σ(sp('u,[i,j])*𝐝.i*𝐝.j, i,1..dim), j,1..dim)
In general we do not require that it be symmetric.
Co-pairing
Solve the "twisted snake relation" as a system of linear equations.
fricas
Ω:𝐋:=Σ(Σ(sb('u,[i,j])*𝐞.i*𝐞.j, i,1..dim), j,1..dim)
fricas
Í :=
( I Ω ) /
( I X ) /
( U I )
fricas
Ì:=
( Ω I ) /
( X I ) /
( I U )
fricas
equate(f,g)==map((x,y)+->(x=y),ravel f, ravel g);
Type: Void
fricas
eq1:=equate(Í,I)
fricas
Compiling function equate with type (LinearOperator(
OrderedVariableList([1,2]),Expression(Integer)), LinearOperator(
OrderedVariableList([1,2]),Expression(Integer))) -> List(Equation
(Expression(Integer)))Type: List(Equation(Expression(Integer)))
fricas
eq2:=equate(Ì,I)
Type: List(Equation(Expression(Integer)))
fricas
snake:=solve(concat(eq1,eq2),concat Ξ(Ξ(sb('u,[i,j]), i,1..dim), j,1..dim));
Type: List(List(Equation(Expression(Integer))))
fricas
if #snake ~= 1 then error "no solution"
Type: Void
fricas
Ω:=eval(Ω,snake(1))
fricas
matrix Ξ(Ξ(Ω/(𝐝.i*𝐝.j), i,1..dim), j,1..dim)
This is equivalent to a matrix inverse (transposed!)
fricas
Um:=matrix Ξ(Ξ((𝐞.i*𝐞.j)/U, i,1..dim), j,1..dim)
fricas
mU:=inverse map(retract,Um)
Type: Union(Matrix(Expression(Integer)),...)
fricas
Ωm:=Σ(Σ(mU(i,j)*(𝐞.i*𝐞.j), i,1..dim), j,1..dim)
fricas
-- compare
test(Ω=Ωm)
Type: Boolean
Check that the twisted snake relation holds
fricas
test
( I Ω ) /
( I X ) /
( U I ) = I
Type: Boolean
fricas
test
( Ω I ) /
( X I ) /
( I U ) = I
Type: Boolean
Dimension
Since the "snake" is twisted, dimension is as expected.
fricas
d:=
Ω /
U
This "twisted dimension " depends on 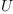 !
!
fricas
d':=
Ω /
X /
U
(0.0,-1.2)(0.8,-1.2)(0.8,-0.4)
\psbezier[linewidth=0.04](0.8,0.4)(0.8,1.2)(1.6,1.2)(1.6,0.4)
\psline[linewidth=0.04cm](0.0,-0.4)(0.0,0.2)
\psline[linewidth=0.04cm](1.6,-0.4)(1.6,-1.0)
\psline[linewidth=0.04cm](2.8,0.2)(2.8,-1.0)
\psbezier[linewidth=0.04](5.8,-0.4)(5.8,-1.2)(5.0,-1.2)(5.0,-0.4)
\psbezier[linewidth=0.04](5.0,0.4)(5.0,1.2)(4.2,1.2)(4.2,0.4)
\psline[linewidth=0.04cm](5.8,-0.4)(5.8,0.2)
\psline[linewidth=0.04cm](4.2,-0.4)(4.2,-1.0)
\usefont{T1}{ptm}{m}{n}
\rput(2.0948439,-0.095){=}
\usefont{T1}{ptm}{m}{n}
\rput(3.4948437,-0.095){=}
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](4.2,0.4)(4.2,-0.2)(5.0,0.2)(5.0,-0.4)
\psbezier[linewidth=0.04](5.0,0.4)(5.0,-0.2)(4.2,0.2)(4.2,-0.4)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](0.8,0.4)(0.8,-0.2)(1.6,0.2)(1.6,-0.4)
\psbezier[linewidth=0.04](1.6,0.4)(1.6,-0.2)(0.8,0.2)(0.8,-0.4)
\psline[linewidth=0.04cm](2.8,1.0)(2.8,0.2)
\psline[linewidth=0.04cm](5.8,1.0)(5.8,0.2)
\psline[linewidth=0.04cm](0.0,1.0)(0.0,0.2)
\end{pspicture}
}
\scalebox{1} % Change this value to rescale the drawing.
{
\begin{pspicture}(0,-1.22)(5.82,1.22)
\psbezier[linewidth=0.04](0.0,-0.4)(0.0,-1.2)(0.8,-1.2)(0.8,-0.4)
\psbezier[linewidth=0.04](0.8,0.4)(0.8,1.2)(1.6,1.2)(1.6,0.4)
\psline[linewidth=0.04cm](0.0,-0.4)(0.0,0.2)
\psline[linewidth=0.04cm](1.6,-0.4)(1.6,-1.0)
\psline[linewidth=0.04cm](2.8,0.2)(2.8,-1.0)
\psbezier[linewidth=0.04](5.8,-0.4)(5.8,-1.2)(5.0,-1.2)(5.0,-0.4)
\psbezier[linewidth=0.04](5.0,0.4)(5.0,1.2)(4.2,1.2)(4.2,0.4)
\psline[linewidth=0.04cm](5.8,-0.4)(5.8,0.2)
\psline[linewidth=0.04cm](4.2,-0.4)(4.2,-1.0)
\usefont{T1}{ptm}{m}{n}
\rput(2.0948439,-0.095){=}
\usefont{T1}{ptm}{m}{n}
\rput(3.4948437,-0.095){=}
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](4.2,0.4)(4.2,-0.2)(5.0,0.2)(5.0,-0.4)
\psbezier[linewidth=0.04](5.0,0.4)(5.0,-0.2)(4.2,0.2)(4.2,-0.4)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](0.8,0.4)(0.8,-0.2)(1.6,0.2)(1.6,-0.4)
\psbezier[linewidth=0.04](1.6,0.4)(1.6,-0.2)(0.8,0.2)(0.8,-0.4)
\psline[linewidth=0.04cm](2.8,1.0)(2.8,0.2)
\psline[linewidth=0.04cm](5.8,1.0)(5.8,0.2)
\psline[linewidth=0.04cm](0.0,1.0)(0.0,0.2)
\end{pspicture}
}](images/2432629302176308249-16.0px.png)
(5.8,-0.9)(5.0,-0.9)(5.0,-0.1)
\psbezier[linewidth=0.04](5.8,-0.1)(5.8,0.7)(5.0,0.7)(5.0,-0.1)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](4.2,0.7)(4.2,0.1)(5.0,0.5)(5.0,-0.1)
\psbezier[linewidth=0.04](5.0,0.1)(5.0,-0.5)(4.2,-0.1)(4.2,-0.7)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](0.0,-0.1)(0.0,-0.9)(0.8,-0.9)(0.8,-0.1)
\psbezier[linewidth=0.04](0.0,-0.1)(0.0,0.7)(0.8,0.7)(0.8,-0.1)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](1.6,0.7)(1.6,0.1)(0.8,0.5)(0.8,-0.1)
\psbezier[linewidth=0.04](0.8,0.1)(0.8,-0.5)(1.6,-0.1)(1.6,-0.7)
\psline[linewidth=0.04cm](2.8,0.3)(2.8,-0.9)
\psline[linewidth=0.04cm](2.8,0.9)(2.8,0.3)
\psline[linewidth=0.04cm](4.2,0.9)(4.2,0.7)
\psline[linewidth=0.04cm](4.2,-0.9)(4.2,-0.7)
\psline[linewidth=0.04cm](1.6,0.9)(1.6,0.7)
\psline[linewidth=0.04cm](1.6,-0.7)(1.6,-0.9)
\usefont{T1}{ptm}{m}{n}
\rput(2.0948439,0.005){=}
\usefont{T1}{ptm}{m}{n}
\rput(3.4948437,0.005){=}
\end{pspicture}
}
\scalebox{1} % Change this value to rescale the drawing.
{
\begin{pspicture}(0,-0.92)(5.82,0.92)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](5.8,-0.1)(5.8,-0.9)(5.0,-0.9)(5.0,-0.1)
\psbezier[linewidth=0.04](5.8,-0.1)(5.8,0.7)(5.0,0.7)(5.0,-0.1)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](4.2,0.7)(4.2,0.1)(5.0,0.5)(5.0,-0.1)
\psbezier[linewidth=0.04](5.0,0.1)(5.0,-0.5)(4.2,-0.1)(4.2,-0.7)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](0.0,-0.1)(0.0,-0.9)(0.8,-0.9)(0.8,-0.1)
\psbezier[linewidth=0.04](0.0,-0.1)(0.0,0.7)(0.8,0.7)(0.8,-0.1)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](1.6,0.7)(1.6,0.1)(0.8,0.5)(0.8,-0.1)
\psbezier[linewidth=0.04](0.8,0.1)(0.8,-0.5)(1.6,-0.1)(1.6,-0.7)
\psline[linewidth=0.04cm](2.8,0.3)(2.8,-0.9)
\psline[linewidth=0.04cm](2.8,0.9)(2.8,0.3)
\psline[linewidth=0.04cm](4.2,0.9)(4.2,0.7)
\psline[linewidth=0.04cm](4.2,-0.9)(4.2,-0.7)
\psline[linewidth=0.04cm](1.6,0.9)(1.6,0.7)
\psline[linewidth=0.04cm](1.6,-0.7)(1.6,-0.9)
\usefont{T1}{ptm}{m}{n}
\rput(2.0948439,0.005){=}
\usefont{T1}{ptm}{m}{n}
\rput(3.4948437,0.005){=}
\end{pspicture}
}](images/2886468678326544459-16.0px.png)
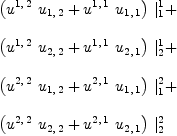
![\label{eq11}\begin{array}{@{}l}
\displaystyle
\left[{{{{u^{1, \: 2}}\ {u_{1, \: 2}}}+{{u^{1, \: 1}}\ {u_{1, \: 1}}}}= 1}, \:{{{{u^{1, \: 2}}\ {u_{2, \: 2}}}+{{u^{1, \: 1}}\ {u_{2, \: 1}}}}= 0}, \: \right.
\
\
\displaystyle
\left.{{{{u^{2, \: 2}}\ {u_{1, \: 2}}}+{{u^{2, \: 1}}\ {u_{1, \: 1}}}}= 0}, \:{{{{u^{2, \: 2}}\ {u_{2, \: 2}}}+{{u^{2, \: 1}}\ {u_{2, \: 1}}}}= 1}\right]
\label{eq11}\begin{array}{@{}l}
\displaystyle
\left[{{{{u^{1, \: 2}}\ {u_{1, \: 2}}}+{{u^{1, \: 1}}\ {u_{1, \: 1}}}}= 1}, \:{{{{u^{1, \: 2}}\ {u_{2, \: 2}}}+{{u^{1, \: 1}}\ {u_{2, \: 1}}}}= 0}, \: \right.
\
\
\displaystyle
\left.{{{{u^{2, \: 2}}\ {u_{1, \: 2}}}+{{u^{2, \: 1}}\ {u_{1, \: 1}}}}= 0}, \:{{{{u^{2, \: 2}}\ {u_{2, \: 2}}}+{{u^{2, \: 1}}\ {u_{2, \: 1}}}}= 1}\right]](images/5250008307464236527-16.0px.png)
![\label{eq12}\begin{array}{@{}l}
\displaystyle
\left[{{{{u^{2, \: 1}}\ {u_{2, \: 1}}}+{{u^{1, \: 1}}\ {u_{1, \: 1}}}}= 1}, \:{{{{u^{2, \: 1}}\ {u_{2, \: 2}}}+{{u^{1, \: 1}}\ {u_{1, \: 2}}}}= 0}, \: \right.
\
\
\displaystyle
\left.{{{{u^{2, \: 2}}\ {u_{2, \: 1}}}+{{u^{1, \: 2}}\ {u_{1, \: 1}}}}= 0}, \:{{{{u^{2, \: 2}}\ {u_{2, \: 2}}}+{{u^{1, \: 2}}\ {u_{1, \: 2}}}}= 1}\right]
\label{eq12}\begin{array}{@{}l}
\displaystyle
\left[{{{{u^{2, \: 1}}\ {u_{2, \: 1}}}+{{u^{1, \: 1}}\ {u_{1, \: 1}}}}= 1}, \:{{{{u^{2, \: 1}}\ {u_{2, \: 2}}}+{{u^{1, \: 1}}\ {u_{1, \: 2}}}}= 0}, \: \right.
\
\
\displaystyle
\left.{{{{u^{2, \: 2}}\ {u_{2, \: 1}}}+{{u^{1, \: 2}}\ {u_{1, \: 1}}}}= 0}, \:{{{{u^{2, \: 2}}\ {u_{2, \: 2}}}+{{u^{1, \: 2}}\ {u_{1, \: 2}}}}= 1}\right]](images/5203550341738782448-16.0px.png)




![]() !
!