login  home  contents  what's new  discussion  bug reports     help  links  subscribe  changes  refresh  edit
FrontPage
SymbolsAndVariables  ← ↑ →  Test14

TaylorSeries
  
last edited 3 years ago by hemmecke

Edit detail for TaylorSeries revision 1 of 8
1 2 3 4 5 6 7 8
Editor: Ralf Hemmecke
Time: 2014/08/23 23:02:08 GMT+0
Note: 
changed:
-
Example for multivariate Taylor series expansion

  In order to work with multivariate Taylor series one first
  has to do a few preparation steps in order to create an
  appropriate domain.

\begin{axiom}
Z==>Integer
Q==>Fraction Z
vl: List Symbol := [x,y]
V==>OrderedVariableList vl
E ==> DirectProduct(2, NonNegativeInteger)
P==>SparseMultivariatePolynomial(Q, V)
M==>SparseMultivariateTaylorSeries(Q,V,P)
X:=monomial(1$M,x,1)
Y:=monomial(1$M,y,1)
sinh(X)*cosh(Y)
\end{axiom}


From BillPage Fri Aug 22 21:19:19 +0000 2014
From: Bill Page
Date: Fri, 22 Aug 2014 21:19:19 +0000
Subject: Naive solution
Message-ID: <20140822211919+0000@axiom-wiki.newsynthesis.org>

This is not what I expected:
\begin{axiom}
x:=taylor 'x
y:=taylor 'y
sinh(x)*cosh(y)
\end{axiom}

Can it be converted somehow to the solution above?

Most simple solution

  There is a domain in FriCAS that is similar to the 'Polynomial(Q)' domain.
  Then the input is as simple as above.

\begin{axiom}
T==>TaylorSeries Fraction Integer
xt:T := 'x
yt:T := 'y
sinh(xt)*cosh(yt)
\end{axiom}

Example for multivariate Taylor series expansion

In order to work with multivariate Taylor series one first has to do a few preparation steps in order to create an appropriate domain.

fricas
Z==>Integer
Type: Void
fricas
Q==>Fraction Z
Type: Void
fricas
vl: List Symbol := [x,y]
\label{eq1}\left[ x , \: y \right](1)
Type: List(Symbol)
fricas
V==>OrderedVariableList vl
Type: Void
fricas
E ==> DirectProduct(2, NonNegativeInteger)
Type: Void
fricas
P==>SparseMultivariatePolynomial(Q, V)
Type: Void
fricas
M==>SparseMultivariateTaylorSeries(Q,V,P)
Type: Void
fricas
X:=monomial(1$M,x,1)
\label{eq2}x(2)
Type: SparseMultivariateTaylorSeries?(Fraction(Integer),OrderedVariableList?([x,y]),SparseMultivariatePolynomial?(Fraction(Integer),OrderedVariableList?([x,y])))
fricas
Y:=monomial(1$M,y,1)
\label{eq3}y(3)
Type: SparseMultivariateTaylorSeries?(Fraction(Integer),OrderedVariableList?([x,y]),SparseMultivariatePolynomial?(Fraction(Integer),OrderedVariableList?([x,y])))
fricas
sinh(X)*cosh(Y)
\label{eq4}\begin{array}{@{}l} \displaystyle x +{\left({{1 \over 6}\ {{x}^{3}}}+{{1 \over 2}\ {{y}^{2}}\ x}\right)}+{\left({{1 \over{120}}\ {{x}^{5}}}+{{1 \over{12}}\ {{y}^{2}}\ {{x}^{3}}}+{{1 \over{24}}\ {{y}^{4}}\ x}\right)}+ \ \ \displaystyle {\left({{1 \over{5040}}\ {{x}^{7}}}+{{1 \over{240}}\ {{y}^{2}}\ {{x}^{5}}}+{{1 \over{144}}\ {{y}^{4}}\ {{x}^{3}}}+{{1 \over{720}}\ {{y}^{6}}\ x}\right)}+ \ \ \displaystyle {\left({ \begin{array}{@{}l} \displaystyle {{1 \over{362880}}\ {{x}^{9}}}+{{1 \over{10080}}\ {{y}^{2}}\ {{x}^{7}}}+{{1 \over{2880}}\ {{y}^{4}}\ {{x}^{5}}}+ \ \ \displaystyle {{1 \over{4320}}\ {{y}^{6}}\ {{x}^{3}}}+{{1 \over{40320}}\ {{y}^{8}}\ x} (4)
Type: SparseMultivariateTaylorSeries?(Fraction(Integer),OrderedVariableList?([x,y]),SparseMultivariatePolynomial?(Fraction(Integer),OrderedVariableList?([x,y])))

Naive solution --Bill Page, Fri, 22 Aug 2014 21:19:19 +0000 reply
This is not what I expected:
fricas
x:=taylor 'x
\label{eq5}x(5)
Type: UnivariateTaylorSeries?(Expression(Integer),x,0)
fricas
y:=taylor 'y
\label{eq6}y(6)
Type: UnivariateTaylorSeries?(Expression(Integer),y,0)
fricas
sinh(x)*cosh(y)
\label{eq7}\begin{array}{@{}l} \displaystyle x +{{1 \over 6}\ {{x}^{3}}}+{{1 \over{120}}\ {{x}^{5}}}+{{1 \over{5 040}}\ {{x}^{7}}}+{{1 \over{362880}}\ {{x}^{9}}}+{O \left({{x}^{11}}\right)}+ \ \ \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle {{1 \over 2}\ x}+{{1 \over{12}}\ {{x}^{3}}}+{{1 \over{240}}\ {{x}^{5}}}+{{1 \over{10080}}\ {{x}^{7}}}+{{1 \over{725760}}\ {{x}^{9}}}+ \ \ \displaystyle {O \left({{x}^{11}}\right)} (7)
Type: UnivariateTaylorSeries?(UnivariateTaylorSeries?(Expression(Integer),x,0),y,0)

Can it be converted somehow to the solution above?

Most simple solution

There is a domain in FriCAS? that is similar to the Polynomial(Q) domain. Then the input is as simple as above.

fricas
T==>TaylorSeries Fraction Integer
Type: Void
fricas
xt:T := 'x
\label{eq8}x(8)
Type: TaylorSeries?(Fraction(Integer))
fricas
yt:T := 'y
\label{eq9}y(9)
Type: TaylorSeries?(Fraction(Integer))
fricas
sinh(xt)*cosh(yt)
\label{eq10}\begin{array}{@{}l} \displaystyle x +{\left({{1 \over 2}\ x \ {{y}^{2}}}+{{1 \over 6}\ {{x}^{3}}}\right)}+{\left({{1 \over{24}}\ x \ {{y}^{4}}}+{{1 \over{12}}\ {{x}^{3}}\ {{y}^{2}}}+{{1 \over{120}}\ {{x}^{5}}}\right)}+ \ \ \displaystyle {\left({{1 \over{720}}\ x \ {{y}^{6}}}+{{1 \over{144}}\ {{x}^{3}}\ {{y}^{4}}}+{{1 \over{240}}\ {{x}^{5}}\ {{y}^{2}}}+{{1 \over{5 040}}\ {{x}^{7}}}\right)}+ \ \ \displaystyle {\left({ \begin{array}{@{}l} \displaystyle {{1 \over{40320}}\ x \ {{y}^{8}}}+{{1 \over{4320}}\ {{x}^{3}}\ {{y}^{6}}}+{{1 \over{2880}}\ {{x}^{5}}\ {{y}^{4}}}+ \ \ \displaystyle {{1 \over{10080}}\ {{x}^{7}}\ {{y}^{2}}}+{{1 \over{362880}}\ {{x}^{9}}} (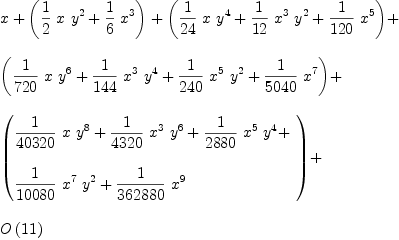10)
Type: TaylorSeries?(Fraction(Integer))