|
|
|
last edited 4 months ago by test1 |
Edit detail for Symbolic Integration revision 1 of 16
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | ||
|
Editor: 127.0.0.1
Time: 2007/11/15 20:25:38 GMT-8 |
||
| Note: transferred from axiom-developer | ||
changed: - Errors in symbolic integration AXIOM Examples 1) \begin{axiom} integrate(sin(x)+sqrt(1-x^3),x) \end{axiom} \begin{reduce} int(sin(x)+sqrt(1-x^3),x); \end{reduce} 2) \begin{axiom} integrate(sqrt(1-log(sin(x)^2)),x) \end{axiom} \begin{reduce} int(sqrt(1-log(sin(x)^2)),x); \end{reduce} 3) \begin{axiom} integrate(sqrt(sin(1/x)),x) \end{axiom} That seems strange given the claims about the "completeness" of Axiom's integration algorithm! But to be fair, Maple also returns this integral unevaluated. \begin{reduce} int(sqrt(sin(1/x)),x); \end{reduce} 4) \begin{axiom} integrate(sqrt(sin(x)),x) \end{axiom} \begin{reduce} int(sqrt(sin(x)),x); \end{reduce} For this Maple 9 gives the following result: \begin{eqnarray} -{\frac {\sqrt {1+\sin \left( x \right) }\sqrt {-2\,\sin \left( x \right) +2}\sqrt {-\sin \left( x \right) }}{\cos \left( x \right) \sqrt {\sin \left( x \right) }}} \times \\ \left( 2\,{\it EllipticE} \left( \sqrt {1+\sin \left( x \right) },1/2\,\sqrt {2} \right) -{\it EllipticF} \left( \sqrt {1+\sin \left( x \right) },1/2\,\sqrt {2} \right) \right) \end{eqnarray} And Mathematica 4 gives: \begin{equation} -2\,{\it EllipticE}(\frac{\frac{\pi }{2} - x}{2},2) \end{equation} From unknown Tue Mar 22 11:48:00 -0600 2005 From: Date: Tue, 22 Mar 2005 11:48:00 -0600 Subject: symbolic integration Message-ID: <20050322114800-0600@page.axiom-developer.org> \begin{axiom} integrate(exp(-x^2),x) \end{axiom} From unknown Wed Mar 23 08:23:21 -0600 2005 From: Date: Wed, 23 Mar 2005 08:23:21 -0600 Subject: Errorfunction Message-ID: <20050323082321-0600@page.axiom-developer.org> \begin{axiom} integrate(exp(-x^2/2)/sqrt(%pi*2),x=%minusInfinity..%plusInfinity) \end{axiom} From unknown Sat May 21 12:49:39 -0500 2005 From: unknown Date: Sat, 21 May 2005 12:49:39 -0500 Subject: Message-ID: <20050521124939-0500@page.axiom-developer.org> \begin{axiom} int(x,x) \end{axiom} From unknown Sat May 21 12:50:47 -0500 2005 From: unknown Date: Sat, 21 May 2005 12:50:47 -0500 Subject: Message-ID: <20050521125047-0500@page.axiom-developer.org> \begin{axiom} integrate(x,x) \end{axiom} From unknown Sat May 21 12:51:59 -0500 2005 From: unknown Date: Sat, 21 May 2005 12:51:59 -0500 Subject: Message-ID: <20050521125159-0500@page.axiom-developer.org> \begin{axiom} axiomintegrate(x^6*exp(-x^2/2)/sqrt(%pi*2),x=%minusInfinity..%plusInfinity) \end{axiom} From unknown Sat May 21 12:52:20 -0500 2005 From: unknown Date: Sat, 21 May 2005 12:52:20 -0500 Subject: Message-ID: <20050521125220-0500@page.axiom-developer.org> \begin{axiom} integrate(x^6*exp(-x^2/2)/sqrt(%pi*2),x=%minusInfinity..%plusInfinity) \end{axiom} The answer should be: \begin{equation} 15\,{\frac {\sqrt {\pi }}{\sqrt {\pi}}} \end{equation} From unknown Thu Aug 25 05:57:53 -0500 2005 From: unknown Date: Thu, 25 Aug 2005 05:57:53 -0500 Subject: integrate(exp(x)/x^2) Message-ID: <20050825055753-0500@page.axiom-developer.org> Axiom does not perform the integration (while it perform the integration of exp(x)/x ), but the integration can be given in terms of Ei(x) integrate(exp(x)/x^2,x) --> Ei(x)-exp(x)/x From unknown Sat Oct 22 19:04:53 -0500 2005 From: unknown Date: Sat, 22 Oct 2005 19:04:53 -0500 Subject: Message-ID: <20051022190453-0500@page.axiom-developer.org> int(sqrt(x), x)
Errors in symbolic integration
AXIOM Examples
1)
axiom
integrate(sin(x)+sqrt(1-x^3),x)
| (1) |
Type: Union(Expression(Integer),
int(sin(x)+sqrt(1-x^3),x); | reduce |
2)
axiom
integrate(sqrt(1-log(sin(x)^2)),x)
>> Error detected within library code: integrate: implementation incomplete (constant residues)
int(sqrt(1-log(sin(x)^2)),x); | reduce |
3)
axiom
integrate(sqrt(sin(1/x)),x)
>> Error detected within library code: integrate: implementation incomplete (constant residues)
That seems strange given the claims about the "completeness" of Axiom's integration algorithm! But to be fair, Maple also returns this integral unevaluated.
int(sqrt(sin(1/x)),x); | reduce |
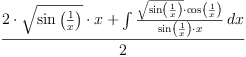 |
4)
axiom
integrate(sqrt(sin(x)),x)
| (2) |
Type: Union(Expression(Integer),
int(sqrt(sin(x)),x); | reduce |
For this Maple 9 gives the following result:
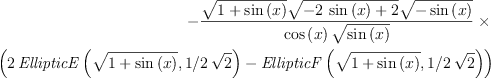 | (3) |
And Mathematica 4 gives:
| (4) |
- symbolic integration
- Tue, 22 Mar 2005 11:48:00 -0600 reply
axiomintegrate(exp(-x^2),
x) 
(5) Type: Union(Expression(Integer),...) Errorfunction- Wed, 23 Mar 2005 08:23:21 -0600 reply
axiomintegrate(exp(-x^2/2)/sqrt(%pi*2),
x=%minusInfinity..%plusInfinity) 
(6) Type: Union(f1: OrderedCompletion?(Expression(Integer)),...)
axiom
int(x,x)
There are no exposed library operations named int but there are 5 unexposed operations with that name. Use HyperDoc Browse or issue )display op int to learn more about the available operations.
Cannot find a definition or applicable library operation named int with argument type(s) Variable(x) Variable(x)
Perhaps you should use "@" to indicate the required return type,or "$" to specify which version of the function you need.
axiom
integrate(x,x)
| (7) |
Type: Polynomial(Fraction(Integer))
axiom
axiomintegrate(x^6*exp(-x^2/2)/sqrt(%pi*2),x=%minusInfinity..%plusInfinity)
There are no library operations named axiomintegrate Use HyperDoc Browse or issue )what op axiomintegrate to learn if there is any operation containing " axiomintegrate " in its name.
Cannot find a definition or applicable library operation named axiomintegrate with argument type(s) Expression(Integer) SegmentBinding(OrderedCompletion(Integer))
Perhaps you should use "@" to indicate the required return type,or "$" to specify which version of the function you need.
axiom
integrate(x^6*exp(-x^2/2)/sqrt(%pi*2),x=%minusInfinity..%plusInfinity)
| (8) |
Type: Union(fail: failed,
| (9) |
integrate(exp(x)/x^2,x) --> Ei(x)-exp(x)/x
int(sqrt(x), x)