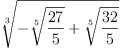Some demo involving the algebraic number fricas (1) -> t1 := (sqrt(3)-3)*(sqrt(3)+1)/6
Type: AlgebraicNumber?
fricas tt1 := -1/sqrt(3)
Type: AlgebraicNumber?
fricas t2 := sqrt(3)/6
Type: AlgebraicNumber?
fricas t1+t2
Type: AlgebraicNumber?
fricas tt1+t2
Type: AlgebraicNumber?
Note that in PanAxiom the above are not generic expressions but of type AlgebraicNumber?. Alternatively, we could also use Renaud Rioboo's fricas RAN ==> RECLOS FRAC INT Type: Void
fricas x1 := (sqrt(3)$RAN-3)*(sqrt(3)$RAN+1)/6
Type: RealClosure(Fraction(Integer))
fricas xx1 := -1/sqrt(3)$RAN
Type: RealClosure(Fraction(Integer))
fricas (x1=xx1)@Boolean
Type: Boolean
It's preferable to give names to the roots: fricas s3 := sqrt(3)$RAN
Type: RealClosure(Fraction(Integer))
fricas (s3-3)*(s3+1)/6
Type: RealClosure(Fraction(Integer))
AlgebraicNumber? doesn't like the following: fricas f3 := sqrt(3,
Type: RealClosure(Fraction(Integer))
fricas f25 := sqrt(1/25,
Type: RealClosure(Fraction(Integer))
fricas f32 := sqrt(32/5, Type: RealClosure(Fraction(Integer))
fricas f27 := sqrt(27/5, Type: RealClosure(Fraction(Integer))
fricas expr1 := sqrt(f32-f27,
Type: RealClosure(Fraction(Integer))
fricas expr2 := (1+f3-f3^2)
Type: RealClosure(Fraction(Integer))
fricas expr1 - f25*expr2
Type: RealClosure(Fraction(Integer))
Although the main point of fricas s := sqrt(190)$RAN+sqrt(1751)$RAN-sqrt(208)$RAN-sqrt(1698)$RAN
Type: RealClosure(Fraction(Integer))
fricas approximate(s,
Type: Float
But we get the same without 'RECLOS': fricas t := sqrt(190)+sqrt(1751)-sqrt(208)-sqrt(1698)
Type: AlgebraicNumber?
fricas digits(30); Type: PositiveInteger?
fricas numeric t - approximate(s,
Type: Float
|
|
|
|
last edited 17 years ago by hemmecke |