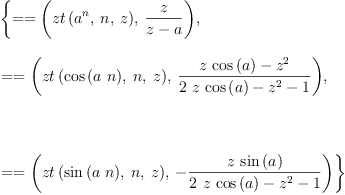MathAction SandBoxZtransform

Topics

FrontPage
- SandBox
  - SandBoxZtransform <-- You are here.

Alasdair McAndrew? writes:

    I'd be grateful for a little help here!  (Then I'll see if I can use the
    z-transform to solve some difference equations.)

Ref:

On 29 May 2007 14:21:26 +0200 Martin Rubey wrote:

It seems that you hit a bug, but fortunately, there is an easy workaround. The problem is with rules of the form:

  rule ...a...b... | p(a,b) == ...

It seems that in this case, the predicate p is never tested, who knows why?

The workaround is to use the "suchThat" function.

fricas

Expr ==> Expression Integer

Type: Void

fricas

zt:=operator 'zt

$\label{eq1}zt$

(1)

Type: BasicOperator?

fricas

ztransrules :=  ruleset([                                            _
  suchThat(rule zt(a^n,n,z) == z/(z-a),                              _
                [a, n], l +-> freeOf?(l.1, l.2)),                    _
  suchThat(rule zt(cos(a*n),n,z) == z*(z-cos(a))/(1-2*z*cos(a)+z^2), _
                [a, n], l +-> freeOf?(l.1, l.2)),                    _
  suchThat(rule zt(sin(a*n),n,z) == z*sin(a)/(1-2*z*cos(a)+z^2),     _
                [a, n], l +-> freeOf?(l.1, l.2))                     _
])$Ruleset(Integer, Integer, Expr)

$\label{eq2}\begin{array}{@{}l} \displaystyle \left\{{= = \left({{zt \left({{{a}^{n}}, \: n , \: z}\right)}, \:{z \over{z - a}}}\right)}, \: \right. \ \ \displaystyle \left.{= = \left({{zt \left({{\cos \left({a \ n}\right)}, \: n , \: z}\right)}, \:{{{z \ {\cos \left({a}\right)}}-{{z}^{2}}}\over{{2 \ z \ {\cos \left({a}\right)}}-{{z}^{2}}- 1}}}\right)}, \: \right. \ \ \displaystyle \left.{= = \left({{zt \left({{\sin \left({a \ n}\right)}, \: n , \: z}\right)}, \: -{{z \ {\sin \left({a}\right)}}\over{{2 \ z \ {\cos \left({a}\right)}}-{{z}^{2}}- 1}}}\right)}\right\}$

(2)

Type: Ruleset(Integer,Integer,Expression(Integer))

We only need to use a rules to handle the case of a^n, sin and cos, but similar rules could be written for the rest or we can do the same thing by common recursive methods:

fricas

ztrans(f:Expr,n:Symbol,z:Symbol):Expr ==
  freeOf?(f,n) => f*z/(z-1)
  fs:= isPlus f; not (fs case "failed") =>
    reduce(+,map(x+->ztrans(x,n,z),fs::List Expr))
  fp:= isTimes f; not (fp case "failed") =>
    reduce(*,select(x+->freeOf?(x,n),fp::List Expr))* _
      ztrans(reduce(*,remove(x+->freeOf?(x,n),fp::List Expr)),n,z)
  fx:=isPower f; if not (fx case "failed") then
     fr:=fx::Record(val:Expr,exponent:Integer)
     k:=fr.exponent
     if fr.val=n and k>0 then
       return (-1)^k*limit(D(z/(z-exp(-x)),[x for i in 1..k]),x=0)::Expression Integer
  ztransrules zt(f,n,z)

   Function declaration ztrans : (Expression(Integer), Symbol, Symbol)
       -> Expression(Integer) has been added to workspace.

Type: Void

On Tue, 29 May 2007 09:19:42 +1000 Alasdair McAndrew? wrote:

1) The commands:

fricas

ztrans(2+3^n,n,z)

fricas

Compiling function ztrans with type (Expression(Integer), Symbol, 
      Symbol) -> Expression(Integer)

$\label{eq3}{{3 \ {{z}^{2}}}-{7 \ z}}\over{{{z}^{2}}-{4 \ z}+ 3}$

(3)

Type: Expression(Integer)

fricas

--should return the result:
2*z/(z-1) + z/(z-3)

$\label{eq4}{{3 \ {{z}^{2}}}-{7 \ z}}\over{{{z}^{2}}-{4 \ z}+ 3}$

(4)

Type: Fraction(Polynomial(Integer))

fricas

ztrans(0,n,z)

$\label{eq5}0$

(5)

Type: Expression(Integer)

fricas

--should return the result:
0

$\label{eq6}0$

(6)

Type: NonNegativeInteger?

fricas

ztrans((-1)^n,n,z)

$\label{eq7}z \over{z + 1}$

(7)

Type: Expression(Integer)

fricas

--should return the result:
z/(z+1)

$\label{eq8}z \over{z + 1}$

(8)

Type: Fraction(Polynomial(Integer))

fricas

ztrans(1,n,z)

$\label{eq9}z \over{z - 1}$

(9)

Type: Expression(Integer)

fricas

--should return the result:
z/(z-1)

$\label{eq10}z \over{z - 1}$

(10)

Type: Fraction(Polynomial(Integer))

fricas

ztrans(n,n,z)

$\label{eq11}z \over{{{z}^{2}}-{2 \ z}+ 1}$

(11)

Type: Expression(Integer)

fricas

--should return the result:
z/(z-1)^2

$\label{eq12}z \over{{{z}^{2}}-{2 \ z}+ 1}$

(12)

Type: Fraction(Polynomial(Integer))

fricas

ztrans(n^2,n,z)

$\label{eq13}{{{z}^{2}}+ z}\over{{{z}^{3}}-{3 \ {{z}^{2}}}+{3 \ z}- 1}$

(13)

Type: Expression(Integer)

fricas

--should return the result:
z*(z+1)/(z-1)^3

$\label{eq14}{{{z}^{2}}+ z}\over{{{z}^{3}}-{3 \ {{z}^{2}}}+{3 \ z}- 1}$

(14)

Type: Fraction(Polynomial(Integer))

fricas

ztrans(n^3,n,z)

$\label{eq15}{{{z}^{3}}+{4 \ {{z}^{2}}}+ z}\over{{{z}^{4}}-{4 \ {{z}^{3}}}+{6 \ {{z}^{2}}}-{4 \ z}+ 1}$

(15)

Type: Expression(Integer)

fricas

--should return the result:
z*(z^2+4*z+1)/(z-1)^4

$\label{eq16}{{{z}^{3}}+{4 \ {{z}^{2}}}+ z}\over{{{z}^{4}}-{4 \ {{z}^{3}}}+{6 \ {{z}^{2}}}-{4 \ z}+ 1}$

(16)

Type: Fraction(Polynomial(Integer))

fricas

ztrans(b^n,n,z)

$\label{eq17}z \over{z - b}$

(17)

Type: Expression(Integer)

fricas

--should return the result:
z/(z-b)

$\label{eq18}z \over{z - b}$

(18)

Type: Fraction(Polynomial(Integer))

fricas

ztrans(cos(b*n),n,z)

$\label{eq19}{{z \ {\cos \left({b}\right)}}-{{z}^{2}}}\over{{2 \ z \ {\cos \left({b}\right)}}-{{z}^{2}}- 1}$

(19)

Type: Expression(Integer)

fricas

--should return the result:
z*(z-cos(b))/(1-2*z*cos(b)+z^2)

$\label{eq20}{{z \ {\cos \left({b}\right)}}-{{z}^{2}}}\over{{2 \ z \ {\cos \left({b}\right)}}-{{z}^{2}}- 1}$

(20)

Type: Expression(Integer)

fricas

ztrans(sin(b*n),n,z)

$\label{eq21}-{{z \ {\sin \left({b}\right)}}\over{{2 \ z \ {\cos \left({b}\right)}}-{{z}^{2}}- 1}}$

(21)

Type: Expression(Integer)

fricas

--should return the result:
z*sin(b)/(1-2*z*cos(b)+z^2)

$\label{eq22}-{{z \ {\sin \left({b}\right)}}\over{{2 \ z \ {\cos \left({b}\right)}}-{{z}^{2}}- 1}}$

(22)

Type: Expression(Integer)

2) How do I force answers to be returned in factored form?

fricas

( x+->factor(numer(x))/factor(denom(x)) ) ztrans(2+3^n,n,z)

$\label{eq23}{z \ {\left({3 \ z}- 7 \right)}}\over{{\left(z - 3 \right)}\ {\left(z - 1 \right)}}$

(23)

Type: Fraction(Factored(SparseMultivariatePolynomial?(Integer,Kernel(Expression(Integer)))))

Bill Page wrote:

Reduce does z-transforms

http://www.uni-koeln.de/REDUCE/3.6/doc/ztrans/ztrans.html

load_package ztrans;

*** binomial already defined as operator 

*** ~f already defined as operator

reduce

ztrans((-1)^n*n^2,n,z);

reduce

$\displaylines{\qdd \frac{z\cdot \(-z +1$

ztrans(cos(n*omega*t),n,z);

reduce

$\displaylines{\qdd \frac{z\cdot \(\cos \(\omega \cdot t$

ztrans(cos(b*(n+2))/(n+2),n,z);

reduce

$\displaylines{\qdd z\cdot \(-\cos \(b$

ztrans(n*cos(b*n)/factorial(n),n,z);

reduce

$\displaylines{\qdd \frac{e^{\frac{\cos \(b$

ztrans(sum(1/factorial(k),k,0,n),n,z);

reduce

$\displaylines{\qdd \frac{e^{\frac{1}{ z}}\cdot z}{ z -1} \cr}$

operator f$

ztrans((1+n)^2*f(n),n,z);

reduce

$\displaylines{\qdd \frac{\partial ^{2}ztrans \(f \(n$

Inverse z-transforms

invztrans((z^2-2*z)/(z^2-4*z+1),z,n);

reduce

$\displaylines{\qdd \frac{\(- \sqrt{3} +2$

invztrans(z/((z-a)*(z-b)),z,n);

reduce

$\displaylines{\qdd \frac{a^{n} -b^{n}}{ a -b} \cr}$

invztrans(z/((z-a)*(z-b)*(z-c)),z,n);

reduce

$\displaylines{\qdd \frac{a^{n}\cdot b -a^{n}\cdot c -b^{n}\cdot a +b^{n}\cdot c +c^{n}\cdot a -c^{n}\cdot b}{ a^{2}\cdot b -a^{2}\cdot c -a\cdot b^{2} +a\cdot c^{2} +b^{2}\cdot c -b\cdot c^{2}} \cr}$

invztrans(z*log(z/(z-a)),z,n);

reduce

$\displaylines{\qdd \frac{a^{n}\cdot \(-1$

invztrans(e^(1/(a*z)),z,n);

reduce

$\displaylines{\qdd \frac{1}{ a^{n}\cdot factorial \(n$

invztrans(z*(z-cosh(a))/(z^2-2*z*cosh(a)+1),z,n);

reduce

$\displaylines{\qdd cosh \(a\cdot n$