help links subscribe changes refresh edit

	SandBox
SandBox ProblemSolving ←	↑	→ SandBox Reflection in Aldor

SandBox Qubic

Edit detail for SandBox Qubic revision 1 of 1

	1
Editor: Time: 2007/11/18 18:32:43 GMT-8
Note:

changed:
-
\begin{axiom}
digits 20
-- n:=x^3+a1*x^2+a2*x+a3 ::Polynomial Fraction Integer

Q:=(3*a2-a1^2)/9
R:=(9*a1*a2-27*a3-2*a1^3)/54
S:=(R+(Q^3+R^2)^(1/2))^(1/3)
T:=(R-(Q^3+R^2)^(1/2))^(1/3)
x1:=S+T-a1/3
x2:=-(S+T)/2-a1/3 + %i*sqrt(3)*(S-T)/2
x3:=-(S+T)/2-a1/3 - %i*sqrt(3)*(S-T)/2 

a5:=x^3+a1*x^2+a2*x+a3 ::Polynomial AlgebraicNumber
a6:=(x-x11)  ::Polynomial AlgebraicNumber;

a7:=monicDivide(a5,a6,x) ;

a77:=a7.quotient;
a78:=a7.remainder;

qu1 :=eval(a77,x11,x1)
rem1:=eval(a78,x11,x1)
eval(rem1,[a3=1.0, a2=1.0, a1=1.0])
\end{axiom}



From wyscc Mon Nov 14 02:53:03 -0600 2005
From: wyscc
Date: Mon, 14 Nov 2005 02:53:03 -0600
Subject: 
Message-ID: <20051114025303-0600@page.axiom-developer.org>

How about this:

\begin{axiom}
pkg:= SOLVEFOR(UP('x,Complex Float), Complex Float)
root := aCubic(1,1,1,1)$pkg
qfactor := monicDivide(x^3 + x^2 + x + 1,x - root)
qfactor.quotient
qfactor.remainder
\end{axiom}


From unknown Mon Jan 30 11:54:36 -0600 2006
From: unknown
Date: Mon, 30 Jan 2006 11:54:36 -0600
Subject: 
Message-ID: <20060130115436-0600@wiki.axiom-developer.org>

$$
myeq := (x-9)^3-(x/2)^2+13*x 
$$

fricas

(1) -> digits 20

$\label{eq1}20$

(1)

Type: PositiveInteger?

fricas

-- n:=x^3+a1*x^2+a2*x+a3 ::Polynomial Fraction Integer

Q:=(3*a2-a1^2)/9

$\label{eq2}{{\frac{1}{3}}\ a 2}-{{\frac{1}{9}}\ {{a 1}^{2}}}$

(2)

Type: Polynomial(Fraction(Integer))

fricas

R:=(9*a1*a2-27*a3-2*a1^3)/54

$\label{eq3}-{{\frac{1}{2}}\ a 3}+{{\frac{1}{6}}\ a 1 \ a 2}-{{\frac{1}{2 7}}\ {{a 1}^{3}}}$

(3)

Type: Polynomial(Fraction(Integer))

fricas

S:=(R+(Q^3+R^2)^(1/2))^(1/3)

$\label{eq4}\frac{\root{3}\of{\frac{{9 \ {\sqrt{\frac{{{27}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}{3}$

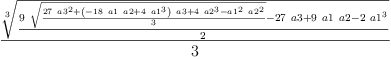(4)

Type: Expression(Integer)

fricas

T:=(R-(Q^3+R^2)^(1/2))^(1/3)

$\label{eq5}\frac{\root{3}\of{\frac{-{9 \ {\sqrt{\frac{{{27}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}{3}$

(5)

Type: Expression(Integer)

fricas

x1:=S+T-a1/3

$\label{eq6}\frac{{\root{3}\of{\frac{{9 \ {\sqrt{\frac{{{27}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}+{\root{3}\of{\frac{-{9 \ {\sqrt{\frac{{{27}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}- a 1}{3}$

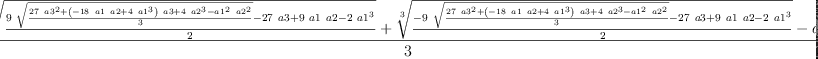(6)

Type: Expression(Integer)

fricas

x2:=-(S+T)/2-a1/3 + %i*sqrt(3)*(S-T)/2

$\label{eq7}\frac{{{\left({i \ {\sqrt{3}}}- 1 \right)}\ {\root{3}\of{\frac{{9 \ {\sqrt{\frac{{{27}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}}+{{\left(-{i \ {\sqrt{3}}}- 1 \right)}\ {\root{3}\of{\frac{-{9 \ {\sqrt{\frac{{{27}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}}-{2 \ a 1}}{6}$

(7)

Type: Expression(Complex(Integer))

fricas

x3:=-(S+T)/2-a1/3 - %i*sqrt(3)*(S-T)/2

$\label{eq8}\frac{{{\left(-{i \ {\sqrt{3}}}- 1 \right)}\ {\root{3}\of{\frac{{9 \ {\sqrt{\frac{{{27}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}}+{{\left({i \ {\sqrt{3}}}- 1 \right)}\ {\root{3}\of{\frac{-{9 \ {\sqrt{\frac{{{27}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}}-{2 \ a 1}}{6}$

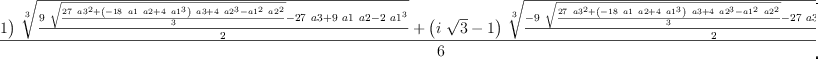(8)

Type: Expression(Complex(Integer))

fricas

a5:=x^3+a1*x^2+a2*x+a3 ::Polynomial AlgebraicNumber

$\label{eq9}{{x}^{3}}+{a 1 \ {{x}^{2}}}+{a 2 \ x}+ a 3$

(9)

Type: Polynomial(AlgebraicNumber?)

fricas

a6:=(x-x11)  ::Polynomial AlgebraicNumber;

Type: Polynomial(AlgebraicNumber?)

fricas

a7:=monicDivide(a5,a6,x) ;

Type: Record(quotient: Polynomial(AlgebraicNumber?),remainder: Polynomial(AlgebraicNumber?))

fricas

a77:=a7.quotient;

Type: Polynomial(AlgebraicNumber?)

fricas

a78:=a7.remainder;

Type: Polynomial(AlgebraicNumber?)

fricas

qu1 :=eval(a77,x11,x1)

$\label{eq10}\frac{{{\root{3}\of{\frac{{9 \ {\sqrt{\frac{{{27}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}^{2}}+{{\left({2 \ {\root{3}\of{\frac{-{9 \ {\sqrt{\frac{{{27}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}}+{3 \ x}+ a 1 \right)}\ {\root{3}\of{\frac{{9 \ {\sqrt{\frac{{{27}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}}+{{\root{3}\of{\frac{-{9 \ {\sqrt{\frac{{{27}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}^{2}}+{{\left({3 \ x}+ a 1 \right)}\ {\root{3}\of{\frac{-{9 \ {\sqrt{\frac{{{2 7}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}}+{9 \ {{x}^{2}}}+{6 \ a 1 \ x}+{9 \ a 2}-{2 \ {{a 1}^{2}}}}{9}$

(10)

Type: Expression(Integer)

fricas

rem1:=eval(a78,x11,x1)

$\label{eq11}\frac{{{\root{3}\of{\frac{-{9 \ {\sqrt{\frac{{{27}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}\ {{\root{3}\of{\frac{{9 \ {\sqrt{\frac{{{27}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}^{2}}}+{{\left({{\root{3}\of{\frac{-{9 \ {\sqrt{\frac{{{2 7}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}^{2}}+{3 \ a 2}-{{a 1}^{2}}\right)}\ {\root{3}\of{\frac{{9 \ {\sqrt{\frac{{{2 7}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}}+{{\left({3 \ a 2}-{{a 1}^{2}}\right)}\ {\root{3}\of{\frac{-{9 \ {\sqrt{\frac{{{2 7}\ {{a 3}^{2}}}+{{\left(-{{18}\ a 1 \ a 2}+{4 \ {{a 1}^{3}}}\right)}\ a 3}+{4 \ {{a 2}^{3}}}-{{{a 1}^{2}}\ {{a 2}^{2}}}}{3}}}}-{{27}\ a 3}+{9 \ a 1 \ a 2}-{2 \ {{a 1}^{3}}}}{2}}}}}{9}$

(11)

Type: Expression(Integer)

fricas

eval(rem1,[a3=1.0, a2=1.0, a1=1.0])

$\label{eq12}0.4 E - 20$

(12)

Type: Expression(Float)

... --wyscc, Mon, 14 Nov 2005 02:53:03 -0600 reply

How about this:

fricas

pkg:= SOLVEFOR(UP('x,Complex Float), Complex Float)

   The constructor SOLVEFOR takes 3 arguments and you have given  2  .

... --unknown, Mon, 30 Jan 2006 11:54:36 -0600 reply