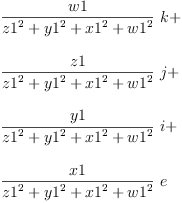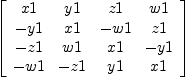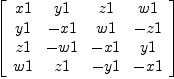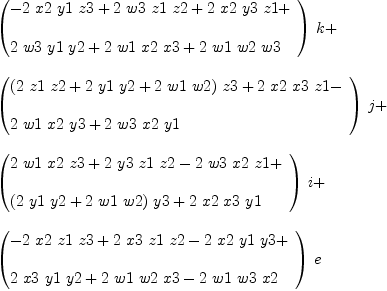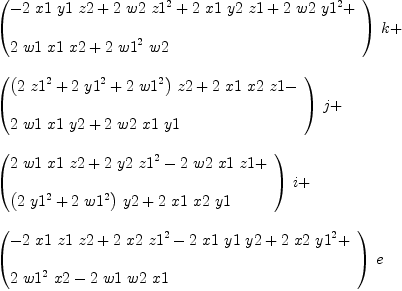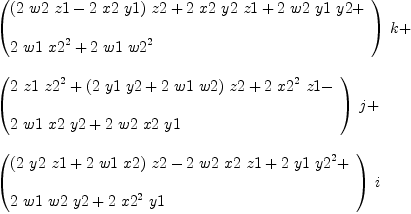Ref: http://arxiv.org/abs/0711.3220 Fourvector algebra Author: Diego Saa (Submitted on 20 Nov 2007) Abstract: The algebra of fourvectors is described. The fourvectors are more appropriate than the Hamilton quaternions for its use in Physics and the sciences in general. The fourvectors embrace the 3D vectors in a natural form. It is shown the excellent ability to perform rotations with the use of fourvectors, as well as their use in relativity for producing Lorentz boosts, which are understood as simple rotations. fricas (1) -> _*_*(x, Type: Void
fricas e:Vector INT:=[1,
Type: Vector(Integer)
fricas i:Vector INT:=[0,
Type: Vector(Integer)
fricas j:Vector INT:=[0,
Type: Vector(Integer)
fricas k:Vector INT:=[0,
Type: Vector(Integer)
fricas test(e**e=e) and _ test(i**i=e) and _ test(j**j=e) and _ test(k**k=e) and _ test(e**i=i) and _ test(e**j=j) and _ test(e**k=k) and _ test(i**e=-i) and _ test(j**e=-j) and _ test(k**e=-k) and _ test(i**j=k) and _ test(j**i=-k) and _ test(k**i=j) and _ test(i**k=-j) and _ test(j**k=i) and _ test(k**j=-i) fricas Compiling function ** with type (Vector(Integer),
Type: Boolean
Axiom has a domain for NonAssociative? Algebra This is documented in the article: Computations in Algebras of Fixed Rank by Johannes Grabmeir and Robert Wisbauer, from the book "Computational Algebra" By Klaus G. Fischer, Philippe Loustaunau, Jay Shapiro. The algebra above can be given by structural constants. fricas )clear all Type: Vector(Matrix(Fraction(Integer)))
fricas V:=AlgebraGivenByStructuralConstants(Fraction Integer,
Type: Type
Multiplication fricas a:=basis()$V
Type: Vector(AlgebraGivenByStructuralConstants?(Fraction(Integer),
fricas matrix([[(a.i * a.j) for j in 1..4] for i in 1..4])$OutputForm
Type: OutputForm?
Commutator and Associator fricas matrix([[commutator(a.x,
Type: OutputForm?
fricas [matrix([[associator(a.x,
Type: List(OutputForm?)
fricas for x in 1..4 repeat
for y in 1..4 repeat
for z in 1..4 repeat
if associator(a.x,
Type: Void
Volume form? fricas a.2 * (a.3 * a.4) = (a.2 * a.3) * a.4
Type: Equation(AlgebraGivenByStructuralConstants?(Fraction(Integer),
Check standard properties fricas leftUnit()$V
Type: Union(AlgebraGivenByStructuralConstants?(Fraction(Integer),
fricas rightUnit()$V
Type: Union("failed",
fricas alternative?()$V
Type: Boolean
fricas leftAlternative?()$V
Type: Boolean
fricas rightAlternative?()$V
Type: Boolean
fricas associative?()$V
Type: Boolean
fricas antiAssociative?()$V
Type: Boolean
fricas --powerAssociative?()$V commutative?()$V
Type: Boolean
fricas antiCommutative?()$V
Type: Boolean
fricas jordanAlgebra?()$V
Type: Boolean
fricas jordanAdmissible?()$V
Type: Boolean
fricas noncommutativeJordanAlgebra?()$V
Type: Boolean
fricas lieAlgebra?()$V
Type: Boolean
fricas lieAdmissible?()$V
Type: Boolean
fricas jacobiIdentity?()$V
Type: Boolean
Commuting elements fricas V has FramedNonAssociativeAlgebra(Fraction Integer)
Type: Boolean
fricas basisOfCommutingElements()$AlgebraPackage(Fraction Integer,
Type: List(AlgebraGivenByStructuralConstants?(Fraction(Integer),
fricas basisOfCenter()$AlgebraPackage(Fraction Integer,
Type: List(AlgebraGivenByStructuralConstants?(Fraction(Integer),
fricas basisOfCentroid()$AlgebraPackage(Fraction Integer,
Type: List(Matrix(Fraction(Integer)))
fricas basisOfNucleus()$AlgebraPackage(Fraction Integer,
Type: List(AlgebraGivenByStructuralConstants?(Fraction(Integer),
fricas basisOfLeftNucloid()$AlgebraPackage(Fraction Integer,
Type: List(Matrix(Fraction(Integer)))
Symbolic computations fricas G:=GenericNonAssociativeAlgebra(Fraction Integer,
Type: Type
Look for Idempotents fricas conditionsForIdempotents()$G
Type: List(Polynomial(Fraction(Integer)))
fricas gb:=groebnerFactorize %
Type: List(List(Polynomial(Fraction(Integer))))
fricas associatorDependence()$G
Type: List(Vector(Fraction(Polynomial(Fraction(Integer)))))
fricas q:=leftRankPolynomial()$G
Type: SparseUnivariatePolynomial?(Fraction(Polynomial(Fraction(Integer))))
fricas map(factor,
Type: List(Factored(Fraction(Polynomial(Fraction(Integer)))))
fricas rightUnit()$G
Type: Union("failed",
fricas p1:=generic([x1,
Type: GenericNonAssociativeAlgebra?(Fraction(Integer),
fricas p2:=generic([x2,
Type: GenericNonAssociativeAlgebra?(Fraction(Integer),
fricas p3:=generic([x3,
Type: GenericNonAssociativeAlgebra?(Fraction(Integer),
fricas leftRecip(p1)$G
Type: Union(GenericNonAssociativeAlgebra?(Fraction(Integer),
fricas rightRecip(p1)$G
Type: Union("failed",
fricas leftRegularRepresentation(p1)
Type: Matrix(Fraction(Polynomial(Fraction(Integer))))
fricas rightRegularRepresentation(p1)
Type: Matrix(Fraction(Polynomial(Fraction(Integer))))
fricas associator(p1,
Type: GenericNonAssociativeAlgebra?(Fraction(Integer),
fricas associator(p1,
Type: GenericNonAssociativeAlgebra?(Fraction(Integer),
fricas associator(p1,
Type: GenericNonAssociativeAlgebra?(Fraction(Integer),
fricas p1*p1
Type: GenericNonAssociativeAlgebra?(Fraction(Integer),
fricas p1*p2 + p2*p1
Type: GenericNonAssociativeAlgebra?(Fraction(Integer),
fricas p1*(p1*p1)+(p1*p1)*p1
Type: GenericNonAssociativeAlgebra?(Fraction(Integer),
|
|
|
|
last edited 17 years ago by Bill Page |
![\label{eq6}\hbox{\axiomType{AlgebraGivenByStructuralConstants}\ } \left({{\hbox{\axiomType{Fraction}\ } \left({\hbox{\axiomType{Integer}\ }}\right)}, \: 4, \:{\left[ e , \: i , \: j , \: k \right]}, \:{\left[{\left[
\begin{array}{cccc}
1 & 0 & 0 & 0
\
0 & 1 & 0 & 0
\
0 & 0 & 1 & 0
\
0 & 0 & 0 & 1
\label{eq6}\hbox{\axiomType{AlgebraGivenByStructuralConstants}\ } \left({{\hbox{\axiomType{Fraction}\ } \left({\hbox{\axiomType{Integer}\ }}\right)}, \: 4, \:{\left[ e , \: i , \: j , \: k \right]}, \:{\left[{\left[
\begin{array}{cccc}
1 & 0 & 0 & 0
\
0 & 1 & 0 & 0
\
0 & 0 & 1 & 0
\
0 & 0 & 0 & 1](images/6636844770221556907-16.0px.png)
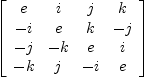
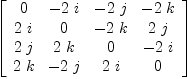



![\label{eq33}\hbox{\axiomType{GenericNonAssociativeAlgebra}\ } \left({{\hbox{\axiomType{Fraction}\ } \left({\hbox{\axiomType{Integer}\ }}\right)}, \: 4, \:{\left[ e , \: i , \: j , \: k \right]}, \:{\left[{\left[
\begin{array}{cccc}
1 & 0 & 0 & 0
\
0 & 1 & 0 & 0
\
0 & 0 & 1 & 0
\
0 & 0 & 0 & 1
\label{eq33}\hbox{\axiomType{GenericNonAssociativeAlgebra}\ } \left({{\hbox{\axiomType{Fraction}\ } \left({\hbox{\axiomType{Integer}\ }}\right)}, \: 4, \:{\left[ e , \: i , \: j , \: k \right]}, \:{\left[{\left[
\begin{array}{cccc}
1 & 0 & 0 & 0
\
0 & 1 & 0 & 0
\
0 & 0 & 1 & 0
\
0 & 0 & 0 & 1](images/6721365432495272960-16.0px.png)