|
|
|
last edited 15 years ago by Mark Clements |
Edit detail for SandBoxMLE revision 1 of 3
| 1 2 3 | ||
|
Editor: Mark Clements
Time: 2008/12/04 15:48:13 GMT-8 |
||
| Note: | ||
changed: - I have recently been experimenting with using Axiom for maximum likelihood estimation, borrowing code (with permission) from "Compact Numerical Methods" by Nash. \begin{spad} )abbrev package OPTIM OptimNash ++ Author: M. Clements ++ Date Created: 24 August 2008 ++ Date Last Updated: ++ Basic Functions: ++ Related Constructors: ++ Also See: ++ AMS Classification: ++ Keywords: ++ References: ++ Description: ++ Numerical optimisation using methods from Nash ++ Permission granted by Nash to translate from his Pascal code to Axiom axisResults ==> Record(X: Vector Float, Fmin:Float, Lowerfun: Boolean) nmminResults ==> Record(X:Vector Float, Fmin:Float, Fail:Boolean) OptimNash: Exports == Implementation where Exports == with Rosen: Vector Float -> Float ++ Rosen(Bvec) returns the Rosen function nmmin: (Vector Float, (Vector Float -> Float), Float) -> nmminResults ++ nmmin(Bvec, fminfn, intol) returns values for the optimised function axissrch :(Vector Float, Vector Float -> Float) -> axisResults ++ axissrch(Bvec, fminfn) returns the axis search method demo: () -> nmminResults ++ demo() returns the rsults of a simple demo using the Rosen function demo2: () -> nmminResults ++ demo2() returns the results of a more complex demo --optimFun: (Expression Float,List Equation Expression Float) -> nmminResults Implementation == add --writeln('Classical starting point (-1.2,1)') Rosen(Bvec: Vector Float):Float == (Bvec(2)-Bvec(1)**2)**2*100.0+(1.0-Bvec(1))**2 --nmmin(vector([11.0, 1.0]), Rosen$OPTIM, -1.0)$OPTIM nmmin(Bvec: Vector Float, fminfn: Vector Float -> Float, intol: Float):nmminResults == Pcol ==> 27 Prow ==> 26 alpha ==> 1.0 beta ==> 0.5 gamma ==> 2.0 Calceps ==> 1.0e-35 big ==> 1.0e35 -- as per R/src/main/optim.c n : Integer := #Bvec action : String C : Integer calcvert : Boolean convtol : Float f : Float funcount : Integer H : Integer i : Integer j : Integer L : Integer notcomp : Boolean n1 : Integer oldsize : Float P : Matrix Float := new(Prow,Pcol,0.0)--[1..Prow,1..Pcol] shrinkfail: Boolean size : Float step : Float temp : Float trystep : Float VH,VL,VN : Float VR : Float x : Vector Float := Bvec -- ugly declaration --writeln('Nash Algorithm 19 version 2 1988-03-17') --writeln(' Nelder Mead polytope direct search function minimiser') --writeln(confile,'Nash Algorithm 19 version 2 1988-03-17') --writeln(confile,' Nelder Mead polytope direct search function minimiser') fail := false (f,notcomp) := (fminfn(Bvec),false) if notcomp then --writeln('**** Function cannot be evaluated at initial parameters ****') --writeln(confile, -- '**** Function cannot be evaluated at initial parameters ****') fail := true else --writeln('Function value for initial parameters = ',f) --writeln(confile,'Function value for initial parameters = ',f) if intol<0.0 then intol := Calceps funcount := 1 convtol := intol*(abs(f)+intol) --writeln(' Scaled convergence tolerance is ',convtol) --writeln(confile,' Scaled convergence tolerance is ',convtol) n1 := n+1 C := n+2 P(n1,1) := f for i in 1..n repeat P(i,1) := Bvec(i) L := 1 size := 0.0 step := 0.0 for i in 1..n repeat if 0.1*abs(Bvec(i))>step then step := 0.1*abs(Bvec(i)) --writeln('Stepsize computed as ',step) --writeln(confile,'Stepsize computed as ',step) for j in 2..n1 repeat action := "BUILD " for i in 1..n repeat P(i,j) := Bvec(i) trystep := step while P(j-1,j)=Bvec(j-1) repeat P(j-1,j) := Bvec(j-1)+trystep trystep := trystep*10.0 size := size+trystep oldsize := size calcvert := true shrinkfail := false repeat if calcvert then for j in 1..n1 repeat if j~=L then for i in 1..n repeat Bvec(i) := P(i,j) (f,notcomp) := (fminfn(Bvec),false) if notcomp or f>=big then f := big funcount := funcount+1 P(n1,j) := f calcvert := false VL := P(n1,L) VH := VL H := L for j in 1..n1 repeat if j~=L then f := P(n1,j) if f<VL then L := j VL := f if f>VH then H := j VH := f if VH>VL+convtol then --str(funcount:5,tstr) --writeln(action,tstr,' ',VH,' ',VL) --writeln(confile,action,tstr,' ',VH,' ',VL) VN := beta*VL+(1.0-beta)*VH for i in 1..n repeat temp := -P(i,H) for j in 1..n1 repeat temp := temp+P(i,j) P(i,C) := temp/n for i in 1..n repeat Bvec(i) := (1.0+alpha)*P(i,C)-alpha*P(i,H) (f,notcomp) := (fminfn(Bvec),false) if notcomp or f>=big then f := big funcount := funcount+1 action := "REFLECTION " VR := f if VR<VL then P(n1,C) := f for i in 1..n repeat f := gamma*Bvec(i)+(1-gamma)*P(i,C) P(i,C) := Bvec(i) Bvec(i) := f (f,notcomp) := (fminfn(Bvec),false) if notcomp or f>=big then f := big funcount := funcount+1 if f<VR then for i in 1..n repeat P(i,H) := Bvec(i) P(n1,H) := f action := "EXTENSION " else for i in 1..n repeat P(i,H) := P(i,C) P(n1,H) := VR else action := "HI-REDUCTION " if VR<VH then for i in 1..n repeat P(i,H) := Bvec(i) P(n1,H) := VR action := "LO-REDUCTION " for i in 1..n repeat Bvec(i) := (1-beta)*P(i,H)+beta*P(i,C) (f,notcomp) := (fminfn(Bvec),false) if notcomp or f>=big then f := big funcount := funcount+1 if f<P(n1,H) then for i in 1..n repeat P(i,H) := Bvec(i) P(n1,H) := f else if VR>=VH then action := "SHRINK " calcvert := true size := 0.0 for j in 1..n1 repeat if j~=L then for i in 1..n repeat P(i,j) := beta*(P(i,j)-P(i,L))+P(i,L) size := size+abs(P(i,j)-P(i,L)) if size<oldsize then shrinkfail := false oldsize := size else --writeln('Polytope size measure not decreased in shrink') --writeln(confile, -- 'Polytope size measure not decreased in shrink') shrinkfail := true if ((VH<=VL+convtol) or shrinkfail ) then break -- repeat loop --writeln('Exiting from Alg19.pas Nelder Mead polytope minimiser') --writeln(' ',funcount,' function evaluations used') --writeln(confile,'Exiting from Alg19.pas Nelder Mead polytope minimiser') --writeln(confile,' ',funcount,' function evaluations used') fmin := P(n1,L) for i in 1..n repeat x(i) := P(i,L) if shrinkfail then fail := true return [x, fmin, fail] axissrch(Bvec: Vector Float, fminfn: Vector Float -> Float): axisResults == cradius, eps, f, fplus, step, temp, tilt, fmin: Float i : Integer --notcomp : Boolean --writeln('alg20.pas -- axial search') --writeln(confile,'alg20.pas -- axial search') Calceps : Float := 1.0e-35 big : Float := 1.0e35 -- as per R/src/main/optim.c n :Integer := #(Bvec)::NonNegativeInteger::Integer fmin := fminfn(Bvec) eps := Calceps eps := sqrt(eps) --writeln(' Axis':6,' Stepsize ':14,'function + ':14, -- 'function - ':14,' rad. of curv.':14,' tilt') --writeln(confile,' Axis':6,' Stepsize ':14,'function + ':14, -- 'function - ':14,' rad. of curv.':14,' tilt') lowerfn := false for i in 1..n repeat if (not lowerfn) then temp := Bvec(i) step := eps*(abs(temp)+eps) Bvec(i) := temp+step f := fminfn(Bvec) if (f>=big) then f := big --write(i:5,' ',step:12,' ',f:12,' ') --write(confile,i:5,' ',step:12,' ',f:12,' ') if f<fmin then lowerfn := true if (not lowerfn) then fplus := f Bvec(i) := temp-step f := fminfn(Bvec) if f>=big then f := big --write(f:12,' ') write(confile,f:12,' ') if f<fmin then lowerfn := true if (not lowerfn) then Bvec(i) := temp temp := 0.5*(fplus-f)/step fplus := 0.5*(fplus+f-2.0*fmin)/(step*step) if fplus~=0.0 then cradius := 1.0+temp*temp cradius := cradius*sqrt(cradius)/fplus else cradius := big tilt := 45.0*atan(temp)/atan(1.0) --write(cradius:12,' ',tilt:12) --write(confile,cradius:12,' ',tilt:12) --writeln writeln(confile) [Bvec, f, lowerfn] demo(): nmminResults == nmmin([-1.2, 1.0], Rosen, -1.0) demo2(): nmminResults == --banner:='dr1920.pas -- driver for Nelder-Mead minimisation' --startup --fminset(n,B,Workdata) {sets up problem and defines starting -- values of B} lowerfn:Boolean := false --{safety setting} B:Vector Float := [-1.2,1.0] --initial values mynmminResults :nmminResults myaxisResults : axisResults --n :Integer := #(B)::NonNegativeInteger::Integer repeat mytol:=-1.0 --Note: set the tolerance negative to indicate that --procedure must obtain an appropriate value. mynmminResults := nmmin(B,Rosen,mytol) --{minimise the function} --writeln --writeln(confile) --writeln(' Minimum function value found =',Fmin) --writeln(' At parameters') --writeln(confile,' Minimum function value found =',Fmin) --writeln(confile,' At parameters') --for i in 1..n repeat --{ --writeln(' B[',i,']=',X[i]) --writeln(confile,' B[',i,']=',X[i]) --} --{loop to write out parameters} B := mynmminResults.X myaxisResults := axissrch(B, Rosen) --{alg20.pas} lowerfn := myaxisResults.Lowerfun if lowerfn then B := myaxisResults.X --writeln('Lower function value found') --writeln(confile,'Lower function value found') if (not lowerfn) then break return mynmminResults --flush(confile) close(confile) --if infname<>'con' then close(infile) --{dr1920.pas -- Nelder Mead minimisation with axial search} -- optimFun(e:Expression Float,initial:List Equation Expression Float):nmminResults == -- vars := [lhs(x) for x in initial] -- vals := [rhs(x) for x in initial]::Vector Float -- nmmin(vals, (x +-> eval(e, vars, x)), -1) \end{spad} Now, let's try this. \begin{axiom} VF ==> Vector Float nmminResults ==> Record(X:Vector Float, Fmin:Float, Fail:Boolean) optimFun(e:Expression Float,initial:List Equation Expression Float):nmminResults == vars := [lhs(x) for x in initial] vals := [rhs(x) for x in initial]::Vector Float nmmin(vals, (x +-> eval(e, vars, x)), -1)$OPTIM optimFun((b-a**2)**2*100.0+(1.0-a)**2, [a=11.0,b=1.0]) \end{axiom} As an aside: can we calculate an elasticity from logistic regression? \begin{axiom} Y:=exp(alpha+betak*Pk)/(1+exp(alpha+betak*Pk)) D(Y,Pk)/Y D(Y,Pk)/Y/(1-Y) \end{axiom}
I have recently been experimenting with using Axiom for maximum likelihood estimation, borrowing code (with permission) from "Compact Numerical Methods" by Nash.
spad
)abbrev package OPTIM OptimNash
++ Author: M. Clements
++ Date Created: 24 August 2008
++ Date Last Updated:
++ Basic Functions:
++ Related Constructors:
++ Also See:
++ AMS Classification:
++ Keywords:
++ References:
++ Description:
++ Numerical optimisation using methods from Nash
++ Permission granted by Nash to translate from his Pascal code to Axiom
axisResults ==> Record(X: Vector Float, Fmin:Float, Lowerfun: Boolean)
nmminResults ==> Record(X:Vector Float, Fmin:Float, Fail:Boolean)
OptimNash: Exports == Implementation where
Exports == with
Rosen: Vector Float -> Float
++ Rosen(Bvec) returns the Rosen function
nmmin: (Vector Float, (Vector Float -> Float), Float) -> nmminResults
++ nmmin(Bvec, fminfn, intol) returns values for the optimised function
axissrch :(Vector Float, Vector Float -> Float) -> axisResults
++ axissrch(Bvec, fminfn) returns the axis search method
demo: () -> nmminResults
++ demo() returns the rsults of a simple demo using the Rosen function
demo2: () -> nmminResults
++ demo2() returns the results of a more complex demo
--optimFun: (Expression Float,List Equation Expression Float) -> nmminResults
Implementation == add
--writeln('Classical starting point (-1.2,1)')
Rosen(Bvec: Vector Float):Float ==
(Bvec(2)-Bvec(1)**2)**2*100.0+(1.0-Bvec(1))**2
--nmmin(vector([11.0, 1.0]), Rosen$OPTIM, -1.0)$OPTIM
nmmin(Bvec: Vector Float,
fminfn: Vector Float -> Float,
intol: Float):nmminResults ==
Pcol ==> 27
Prow ==> 26
alpha ==> 1.0
beta ==> 0.5
gamma ==> 2.0
Calceps ==> 1.0e-35
big ==> 1.0e35 -- as per R/src/main/optim.c
n : Integer := #Bvec
action : String
C : Integer
calcvert : Boolean
convtol : Float
f : Float
funcount : Integer
H : Integer
i : Integer
j : Integer
L : Integer
notcomp : Boolean
n1 : Integer
oldsize : Float
P : Matrix Float := new(Prow,Pcol,0.0)--[1..Prow,1..Pcol]
shrinkfail: Boolean
size : Float
step : Float
temp : Float
trystep : Float
VH,VL,VN : Float
VR : Float
x : Vector Float := Bvec -- ugly declaration
--writeln('Nash Algorithm 19 version 2 1988-03-17')
--writeln(' Nelder Mead polytope direct search function minimiser')
--writeln(confile,'Nash Algorithm 19 version 2 1988-03-17')
--writeln(confile,' Nelder Mead polytope direct search function minimiser')
fail := false
(f,notcomp) := (fminfn(Bvec),false)
if notcomp then
--writeln('**** Function cannot be evaluated at initial parameters ****')
--writeln(confile,
-- '**** Function cannot be evaluated at initial parameters ****')
fail := true
else
--writeln('Function value for initial parameters = ',f)
--writeln(confile,'Function value for initial parameters = ',f)
if intol<0.0 then intol := Calceps
funcount := 1
convtol := intol*(abs(f)+intol)
--writeln(' Scaled convergence tolerance is ',convtol)
--writeln(confile,' Scaled convergence tolerance is ',convtol)
n1 := n+1
C := n+2
P(n1,1) := f
for i in 1..n repeat P(i,1) := Bvec(i)
L := 1
size := 0.0
step := 0.0
for i in 1..n repeat if 0.1*abs(Bvec(i))>step then step := 0.1*abs(Bvec(i))
--writeln('Stepsize computed as ',step)
--writeln(confile,'Stepsize computed as ',step)
for j in 2..n1 repeat
action := "BUILD "
for i in 1..n repeat P(i,j) := Bvec(i)
trystep := step
while P(j-1,j)=Bvec(j-1) repeat
P(j-1,j) := Bvec(j-1)+trystep
trystep := trystep*10.0
size := size+trystep
oldsize := size
calcvert := true
shrinkfail := false
repeat
if calcvert then
for j in 1..n1 repeat
if j~=L then
for i in 1..n repeat Bvec(i) := P(i,j)
(f,notcomp) := (fminfn(Bvec),false)
if notcomp or f>=big then f := big
funcount := funcount+1
P(n1,j) := f
calcvert := false
VL := P(n1,L)
VH := VL
H := L
for j in 1..n1 repeat
if j~=L then
f := P(n1,j)
if f<VL then
L := j
VL := f
if f>VH then
H := j
VH := f
if VH>VL+convtol then
--str(funcount:5,tstr)
--writeln(action,tstr,' ',VH,' ',VL)
--writeln(confile,action,tstr,' ',VH,' ',VL)
VN := beta*VL+(1.0-beta)*VH
for i in 1..n repeat
temp := -P(i,H)
for j in 1..n1 repeat temp := temp+P(i,j)
P(i,C) := temp/n
for i in 1..n repeat
Bvec(i) := (1.0+alpha)*P(i,C)-alpha*P(i,H)
(f,notcomp) := (fminfn(Bvec),false)
if notcomp or f>=big then f := big
funcount := funcount+1
action := "REFLECTION "
VR := f
if VR<VL then
P(n1,C) := f
for i in 1..n repeat
f := gamma*Bvec(i)+(1-gamma)*P(i,C)
P(i,C) := Bvec(i)
Bvec(i) := f
(f,notcomp) := (fminfn(Bvec),false)
if notcomp or f>=big then f := big
funcount := funcount+1
if f<VR then
for i in 1..n repeat P(i,H) := Bvec(i)
P(n1,H) := f
action := "EXTENSION "
else
for i in 1..n repeat P(i,H) := P(i,C)
P(n1,H) := VR
else
action := "HI-REDUCTION "
if VR<VH then
for i in 1..n repeat P(i,H) := Bvec(i)
P(n1,H) := VR
action := "LO-REDUCTION "
for i in 1..n repeat Bvec(i) := (1-beta)*P(i,H)+beta*P(i,C)
(f,notcomp) := (fminfn(Bvec),false)
if notcomp or f>=big then f := big
funcount := funcount+1
if f<P(n1,H) then
for i in 1..n repeat P(i,H) := Bvec(i)
P(n1,H) := f
else
if VR>=VH then
action := "SHRINK "
calcvert := true
size := 0.0
for j in 1..n1 repeat
if j~=L then
for i in 1..n repeat
P(i,j) := beta*(P(i,j)-P(i,L))+P(i,L)
size := size+abs(P(i,j)-P(i,L))
if size<oldsize then
shrinkfail := false
oldsize := size
else
--writeln('Polytope size measure not decreased in shrink')
--writeln(confile,
-- 'Polytope size measure not decreased in shrink')
shrinkfail := true
if ((VH<=VL+convtol) or shrinkfail ) then break -- repeat loop
--writeln('Exiting from Alg19.pas Nelder Mead polytope minimiser')
--writeln(' ',funcount,' function evaluations used')
--writeln(confile,'Exiting from Alg19.pas Nelder Mead polytope minimiser')
--writeln(confile,' ',funcount,' function evaluations used')
fmin := P(n1,L)
for i in 1..n repeat x(i) := P(i,L)
if shrinkfail then fail := true
return [x, fmin, fail]
axissrch(Bvec: Vector Float, fminfn: Vector Float -> Float): axisResults ==
cradius, eps, f, fplus, step, temp, tilt, fmin: Float
i : Integer
--notcomp : Boolean
--writeln('alg20.pas -- axial search')
--writeln(confile,'alg20.pas -- axial search')
Calceps : Float := 1.0e-35
big : Float := 1.0e35 -- as per R/src/main/optim.c
n :Integer := #(Bvec)::NonNegativeInteger::Integer
fmin := fminfn(Bvec)
eps := Calceps
eps := sqrt(eps)
--writeln(' Axis':6,' Stepsize ':14,'function + ':14,
-- 'function - ':14,' rad. of curv.':14,' tilt')
--writeln(confile,' Axis':6,' Stepsize ':14,'function + ':14,
-- 'function - ':14,' rad. of curv.':14,' tilt')
lowerfn := false
for i in 1..n repeat
if (not lowerfn) then
temp := Bvec(i)
step := eps*(abs(temp)+eps)
Bvec(i) := temp+step
f := fminfn(Bvec)
if (f>=big) then f := big
--write(i:5,' ',step:12,' ',f:12,' ')
--write(confile,i:5,' ',step:12,' ',f:12,' ')
if f<fmin then lowerfn := true
if (not lowerfn) then
fplus := f
Bvec(i) := temp-step
f := fminfn(Bvec)
if f>=big then f := big
--write(f:12,' ') write(confile,f:12,' ')
if f<fmin then lowerfn := true
if (not lowerfn) then
Bvec(i) := temp
temp := 0.5*(fplus-f)/step
fplus := 0.5*(fplus+f-2.0*fmin)/(step*step)
if fplus~=0.0 then
cradius := 1.0+temp*temp
cradius := cradius*sqrt(cradius)/fplus
else
cradius := big
tilt := 45.0*atan(temp)/atan(1.0)
--write(cradius:12,' ',tilt:12)
--write(confile,cradius:12,' ',tilt:12)
--writeln writeln(confile)
[Bvec, f, lowerfn]
demo(): nmminResults ==
nmmin([-1.2, 1.0], Rosen, -1.0)
demo2(): nmminResults ==
--banner:='dr1920.pas -- driver for Nelder-Mead minimisation'
--startup
--fminset(n,B,Workdata) {sets up problem and defines starting
-- values of B}
lowerfn:Boolean := false --{safety setting}
B:Vector Float := [-1.2,1.0] --initial values
mynmminResults :nmminResults
myaxisResults : axisResults
--n :Integer := #(B)::NonNegativeInteger::Integer
repeat
mytol:=-1.0 --Note: set the tolerance negative to indicate that
--procedure must obtain an appropriate value.
mynmminResults := nmmin(B,Rosen,mytol) --{minimise the function}
--writeln
--writeln(confile)
--writeln(' Minimum function value found =',Fmin)
--writeln(' At parameters')
--writeln(confile,' Minimum function value found =',Fmin)
--writeln(confile,' At parameters')
--for i in 1..n repeat
--{
--writeln(' B[',i,']=',X[i])
--writeln(confile,' B[',i,']=',X[i])
--} --{loop to write out parameters}
B := mynmminResults.X
myaxisResults := axissrch(B, Rosen) --{alg20.pas}
lowerfn := myaxisResults.Lowerfun
if lowerfn then
B := myaxisResults.X
--writeln('Lower function value found')
--writeln(confile,'Lower function value found')
if (not lowerfn) then break
return mynmminResults
--flush(confile) close(confile)
--if infname<>'con' then close(infile)
--{dr1920.pas -- Nelder Mead minimisation with axial search}
-- optimFun(e:Expression Float,initial:List Equation Expression Float):nmminResults ==
-- vars := [lhs(x) for x in initial]
-- vals := [rhs(x) for x in initial]::Vector Float
-- nmmin(vals, (x +-> eval(e, vars, x)), -1)
spad
Compiling FriCAS source code from file
/var/zope2/var/LatexWiki/3925042998800764367-25px001.spad using
old system compiler.
OPTIM abbreviates package OptimNash
processing macro definition axisResults ==> Record(X: Vector Float,Fmin: Float,Lowerfun: Boolean)
processing macro definition nmminResults ==> Record(X: Vector Float,Fmin: Float,Fail: Boolean)
------------------------------------------------------------------------
initializing NRLIB OPTIM for OptimNash
compiling into NRLIB OPTIM
compiling exported Rosen : Vector Float -> Float
Time: 0.15 SEC.
compiling exported nmmin : (Vector Float,Vector Float -> Float,Float) -> Record(X: Vector Float,Fmin: Float,Fail: Boolean)
processing macro definition Pcol ==> 27
processing macro definition Prow ==> 26
processing macro definition alpha ==> (elt (Float) float)(One,Zero,10)
processing macro definition beta ==> (elt (Float) float)(5,-1,10)
processing macro definition gamma ==> (elt (Float) float)(2,Zero,10)
processing macro definition Calceps ==> (elt (Float) float)(One,-35,10)
processing macro definition big ==> (elt (Float) float)(One,35,10)
Time: 0.41 SEC.
compiling exported axissrch : (Vector Float,Vector Float -> Float) -> Record(X: Vector Float,Fmin: Float,Lowerfun: Boolean)
Time: 0.08 SEC.
compiling exported demo : () -> Record(X: Vector Float,Fmin: Float,Fail: Boolean)
Time: 0.08 SEC.
compiling exported demo2 : () -> Record(X: Vector Float,Fmin: Float,Fail: Boolean)
Time: 0.01 SEC.
(time taken in buildFunctor: 0)
;;; *** |OptimNash| REDEFINED
;;; *** |OptimNash| REDEFINED
Time: 0.01 SEC.
Warnings:
[1] nmmin: step has no value
[2] nmmin: f has no value
[3] nmmin: VH has no value
[4] nmmin: H has no value
[5] nmmin: funcount has no value
[6] nmmin: shrinkfail has no value
[7] nmmin: n1 has no value
[8] nmmin: L has no value
[9] axissrch: f has no value
[10] axissrch: temp has no value
[11] axissrch: step has no value
[12] axissrch: fplus has no value
Cumulative Statistics for Constructor OptimNash
Time: 0.74 seconds
finalizing NRLIB OPTIM
Processing OptimNash for Browser database:
--------(Rosen ((Float) (Vector (Float))))---------
--------(nmmin (nmminResults (Vector (Float)) (Mapping (Float) (Vector (Float))) (Float)))---------
--------(axissrch (axisResults (Vector (Float)) (Mapping (Float) (Vector (Float)))))---------
--------(demo (nmminResults))---------
--------(demo2 (nmminResults))---------
--->-->OptimNash(constructor): Not documented!!!!
--->-->OptimNash(): Missing Description
------------------------------------------------------------------------
OptimNash is now explicitly exposed in frame initial
OptimNash will be automatically loaded when needed from
/var/zope2/var/LatexWiki/OPTIM.NRLIB/codeNow, let's try this.
axiom
VF ==> Vector Float
Type: Void
axiom
nmminResults ==> Record(X:Vector Float, Fmin:Float, Fail:Boolean)
Type: Void
axiom
optimFun(e:Expression Float,initial:List Equation Expression Float):nmminResults ==
vars := [lhs(x) for x in initial]
vals := [rhs(x) for x in initial]::Vector Float
nmmin(vals, (x +-> eval(e, vars, x)), -1)$OPTIM
Function declaration optimFun : (Expression Float,List Equation
Expression Float) -> Record(X: Vector Float,Fmin: Float,Fail:
Boolean) has been added to workspace.
Type: Void
axiom
optimFun((b-a**2)**2*100.0+(1.0-a)**2, [a=11.0,b=1.0])
axiom
Compiling function optimFun with type (Expression Float,List
Equation Expression Float) -> Record(X: Vector Float,Fmin: Float,
Fail: Boolean)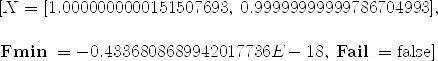 | (1) |
Type: Record(X: Vector Float,Fmin: Float,Fail: Boolean)
As an aside: can we calculate an elasticity from logistic regression?
axiom
Y:=exp(alpha+betak*Pk)/(1+exp(alpha+betak*Pk))
| (2) |
Type: Expression Integer
axiom
D(Y,Pk)/Y
| (3) |
Type: Expression Integer
axiom
D(Y,Pk)/Y/(1-Y)
| (4) |
Type: Expression Integer