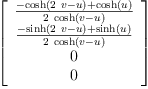MathAction SandBox Idempotent Observers

Topics

FrontPage
- SandBox
  - SandBox Categorical Relativity
    - SandBoxLorentzTransformation
      - SandBox Idempotent Observers <-- You are here.
  - SandBoxNijenhuis
    - SandBox Idempotent Observers <-- You are here.
  - SandBoxObserverAsIdempotent
    - SandBox Idempotent Observers <-- You are here.

Preliminaries

Space-time without reference frames

Lorentz Form (metric) applied to a vector ( $n\times 1$ matrix) produces a co-vector ( $1\times n$ matrix). Scalar and tensor products use matrix multiplication.

fricas

(1) -> ID:=diagonalMatrix [1,1,1,1];

Type: Matrix(Integer)

fricas

G:=diagonalMatrix [-1,1,1,1]

$\label{eq1}\left[ \begin{array}{cccc} - 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1$

(1)

Type: Matrix(Integer)

fricas

Scalar := Expression Integer

$\label{eq2}\hbox{\axiomType{Expression}\ } \left({\hbox{\axiomType{Integer}\ }}\right)$

(2)

Type: Type

fricas

vect(x:List Scalar):Matrix Scalar == matrix map(y+->[y],x)

   Function declaration vect : List(Expression(Integer)) -> Matrix(
      Expression(Integer)) has been added to workspace.

Type: Void

fricas

g(x:Matrix Scalar):Matrix Scalar == transpose(x)*G

   Function declaration g : Matrix(Expression(Integer)) -> Matrix(
      Expression(Integer)) has been added to workspace.

Type: Void

fricas

dot(x:Matrix Scalar,y:Matrix Scalar):Scalar == g(x)*y 

   Function declaration dot : (Matrix(Expression(Integer)), Matrix(
      Expression(Integer))) -> Expression(Integer) has been added to 
      workspace.

Type: Void

fricas

tensor(x:Matrix Scalar,y:Matrix Scalar):Matrix Scalar == x*g(y)

   Function declaration tensor : (Matrix(Expression(Integer)), Matrix(
      Expression(Integer))) -> Matrix(Expression(Integer)) has been 
      added to workspace.

Type: Void

Verification

fricas

htrigs2exp == rule
  cosh(a) == (exp(a)+exp(-a))/2
  sinh(a) == (exp(a)-exp(-a))/2

Type: Void

fricas

sinhcosh == rule
  ?c*exp(a)+?c*exp(-a) == 2*c*cosh(a)
  ?c*exp(a)-?c*exp(-a) == 2*c*sinh(a)
  ?c*exp(a-b)+?c*exp(b-a) == 2*c*cosh(a-b)
  ?c*exp(a-b)-?c*exp(b-a) == 2*c*sinh(a-b)

Type: Void

fricas

expandhtrigs == rule
  cosh(:x+y) == sinh(x)*sinh(y)+cosh(x)*cosh(y)
  sinh(:x+y) == cosh(x)*sinh(y)+sinh(x)*cosh(y)
  cosh(2*x) == 2*cosh(x)^2-1
  sinh(2*x) == 2*sinh(x)*cosh(x)

Type: Void

fricas

expandhtrigs2 == rule
  cosh(2*x+2*y) == 2*cosh(x+y)^2-1
  sinh(2*x+2*y) == 2*sinh(x+y)*cosh(x+y)
  cosh(2*x-2*y) == 2*cosh(x-y)^2-1
  sinh(2*x-2*y) == 2*sinh(x-y)*cosh(x-y)

Type: Void

fricas

Simplify(x:Scalar):Scalar == htrigs sinhcosh simplify htrigs2exp x

   Function declaration Simplify : Expression(Integer) -> Expression(
      Integer) has been added to workspace.

Type: Void

fricas

possible(x)==subst(x, map(y+->(y=(random(100) - random(100))),variables x) )

Type: Void

fricas

is?(eq:Equation Scalar):Boolean == (Simplify(lhs(eq)-rhs(eq))=0)::Boolean

   Function declaration is? : Equation(Expression(Integer)) -> Boolean 
      has been added to workspace.

Type: Void

fricas

Is?(eq:Equation(Matrix(Scalar))):Boolean == _
(map(Simplify,lhs(eq)-rhs(eq)) :: Matrix Expression AlgebraicNumber = _
zero(nrows(lhs(eq)),ncols(lhs(eq)))$Matrix Expression AlgebraicNumber )::Boolean

   Function declaration Is? : Equation(Matrix(Expression(Integer))) -> 
      Boolean has been added to workspace.

Type: Void

Massive Objects

A material object (also referred to as an observer) is represented by a time-like 4-vector

fricas

P:=vect [p0,p1,p2,p3]

fricas

Compiling function vect with type List(Expression(Integer)) -> 
      Matrix(Expression(Integer))

$\label{eq3}\left[ \begin{array}{c} p 0 \ p 1 \ p 2 \ p 3$

(3)

Type: Matrix(Expression(Integer))

fricas

dot(P,P)

fricas

Compiling function g with type Matrix(Expression(Integer)) -> Matrix
      (Expression(Integer))

fricas

Compiling function dot with type (Matrix(Expression(Integer)), 
      Matrix(Expression(Integer))) -> Expression(Integer)

$\label{eq4}{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}$

(4)

Type: Expression(Integer)

fricas

solve(%=-1,p0)

$\label{eq5}\left[{p 0 ={\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}, \:{p 0 = -{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}\right]$

(5)

Type: List(Equation(Expression(Integer)))

fricas

Q:=vect [q0,q1,q2,q3];

Type: Matrix(Expression(Integer))

fricas

S:=1/sqrt(1-s1^2-s2^2-s3^2)*vect [1,-s1,-s2,-s3]

$\label{eq6}\left[ \begin{array}{c} {\frac{1}{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ -{\frac{s 1}{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ -{\frac{s 2}{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ -{\frac{s 3}{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}}$

(6)

Type: Matrix(Expression(Integer))

fricas

dot(S,S)

$\label{eq7}- 1$

(7)

Type: Expression(Integer)

fricas

T:=1/sqrt(1-t1^2-t2^2-t3^2)*vect [1,-t1,-t2,-t3];

Type: Matrix(Expression(Integer))

fricas

W:=1/sqrt(1-w1^2-w2^2-w3^2)*vect [1,-w1,-w2,-w3];

Type: Matrix(Expression(Integer))

fricas

U:=vect [cosh(u),sinh(u),0,0]

$\label{eq8}\left[ \begin{array}{c} {\cosh \left({u}\right)} \ {\sinh \left({u}\right)} \ 0 \ 0$

(8)

Type: Matrix(Expression(Integer))

fricas

simplify dot(U,U)

$\label{eq9}- 1$

(9)

Type: Expression(Integer)

fricas

V:=vect [cosh(v),sinh(v),0,0];

Type: Matrix(Expression(Integer))

Massless Photons

A photon is a represented by a light-like null 4-vector

fricas

A:=vect [a0,a0*a1,a0*a2,a0*a3]

$\label{eq10}\left[ \begin{array}{c} a 0 \ {a 0 \ a 1} \ {a 0 \ a 2} \ {a 0 \ a 3}$

(10)

Type: Matrix(Expression(Integer))

fricas

solve(dot(A,A)=0,a3)

$\label{eq11}\left[{a 3 ={\sqrt{-{{a 2}^{2}}-{{a 1}^{2}}+ 1}}}, \:{a 3 = -{\sqrt{-{{a 2}^{2}}-{{a 1}^{2}}+ 1}}}\right]$

(11)

Type: List(Equation(Expression(Integer)))

fricas

A:=vect [a0,a0*a1,a0*a2,a0*sqrt(1-a1^2-a2^2)]

$\label{eq12}\left[ \begin{array}{c} a 0 \ {a 0 \ a 1} \ {a 0 \ a 2} \ {a 0 \ {\sqrt{-{{a 2}^{2}}-{{a 1}^{2}}+ 1}}}$

(12)

Type: Matrix(Expression(Integer))

fricas

dot(A,A)

$\label{eq13}0$

(13)

Type: Expression(Integer)

fricas

B:=vect [b0,b0*b1,b0*b2,b0*sqrt(1-b1^2-b2^2)]

$\label{eq14}\left[ \begin{array}{c} b 0 \ {b 0 \ b 1} \ {b 0 \ b 2} \ {b 0 \ {\sqrt{-{{b 2}^{2}}-{{b 1}^{2}}+ 1}}}$

(14)

Type: Matrix(Expression(Integer))

fricas

C:=vect [c0,c0*c1,c0*c2,c0*sqrt(1-c1^2-c2^2)]

$\label{eq15}\left[ \begin{array}{c} c 0 \ {c 0 \ c 1} \ {c 0 \ c 2} \ {c 0 \ {\sqrt{-{{c 2}^{2}}-{{c 1}^{2}}+ 1}}}$

(15)

Type: Matrix(Expression(Integer))

Observer "at rest"

fricas

R:=vect [1,0,0,0]

$\label{eq16}\left[ \begin{array}{c} 1 \ 0 \ 0 \ 0$

(16)

Type: Matrix(Expression(Integer))

fricas

dot(R,R)

$\label{eq17}- 1$

(17)

Type: Expression(Integer)

Associated with each such vector is the orthogonal 3-d Euclidean subspace $E_P =\{x | P \cdot x = 0\}$

Relative Velocity

An object P has a unique relative velocity ω(P,Q) with respect to object Q given by

fricas

ω(P,Q)==-P/dot(P,Q)-Q

Type: Void

fricas

map(Simplify, ω(P,Q))

fricas

Compiling function ω with type (Matrix(Expression(Integer)), Matrix(
      Expression(Integer))) -> Matrix(Expression(Integer))

fricas

Compiling body of rule htrigs2exp to compute value of type Ruleset(
      Integer,Integer,Expression(Integer))

fricas

Compiling body of rule sinhcosh to compute value of type Ruleset(
      Integer,Integer,Expression(Integer))

fricas

Compiling function Simplify with type Expression(Integer) -> 
      Expression(Integer)

$\label{eq18}\left[ \begin{array}{c} {\frac{-{p 3 \ q 0 \ q 3}-{p 2 \ q 0 \ q 2}-{p 1 \ q 0 \ q 1}+{p 0 \ {{q 0}^{2}}}- p 0}{{p 3 \ q 3}+{p 2 \ q 2}+{p 1 \ q 1}-{p 0 \ q 0}}} \ {\frac{-{p 3 \ q 1 \ q 3}-{p 2 \ q 1 \ q 2}-{p 1 \ {{q 1}^{2}}}+{p 0 \ q 0 \ q 1}- p 1}{{p 3 \ q 3}+{p 2 \ q 2}+{p 1 \ q 1}-{p 0 \ q 0}}} \ {\frac{-{p 3 \ q 2 \ q 3}-{p 2 \ {{q 2}^{2}}}+{{\left(-{p 1 \ q 1}+{p 0 \ q 0}\right)}\ q 2}- p 2}{{p 3 \ q 3}+{p 2 \ q 2}+{p 1 \ q 1}-{p 0 \ q 0}}} \ {\frac{-{p 3 \ {{q 3}^{2}}}+{{\left(-{p 2 \ q 2}-{p 1 \ q 1}+{p 0 \ q 0}\right)}\ q 3}- p 3}{{p 3 \ q 3}+{p 2 \ q 2}+{p 1 \ q 1}-{p 0 \ q 0}}}$

(18)

Type: Matrix(Expression(Integer))

fricas

map(Simplify, ω(P,R))

$\label{eq19}\left[ \begin{array}{c} 0 \ {\frac{p 1}{p 0}} \ {\frac{p 2}{p 0}} \ {\frac{p 3}{p 0}}$

(19)

Type: Matrix(Expression(Integer))

fricas

map(Simplify, ω(S,T))

$\label{eq20}\left[ \begin{array}{c} {\frac{{{t 3}^{2}}-{s 3 \ t 3}+{{t 2}^{2}}-{s 2 \ t 2}+{{t 1}^{2}}-{s 1 \ t 1}}{{\left({s 3 \ t 3}+{s 2 \ t 2}+{s 1 \ t 1}- 1 \right)}\ {\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}}} \ {\frac{-{s 1 \ {{t 3}^{2}}}+{s 3 \ t 1 \ t 3}-{s 1 \ {{t 2}^{2}}}+{s 2 \ t 1 \ t 2}- t 1 + s 1}{{\left({s 3 \ t 3}+{s 2 \ t 2}+{s 1 \ t 1}- 1 \right)}\ {\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}}} \ {\frac{-{s 2 \ {{t 3}^{2}}}+{s 3 \ t 2 \ t 3}+{{\left({s 1 \ t 1}- 1 \right)}\ t 2}-{s 2 \ {{t 1}^{2}}}+ s 2}{{\left({s 3 \ t 3}+{s 2 \ t 2}+{s 1 \ t 1}- 1 \right)}\ {\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}}} \ {\frac{{{\left({s 2 \ t 2}+{s 1 \ t 1}- 1 \right)}\ t 3}-{s 3 \ {{t 2}^{2}}}-{s 3 \ {{t 1}^{2}}}+ s 3}{{\left({s 3 \ t 3}+{s 2 \ t 2}+{s 1 \ t 1}- 1 \right)}\ {\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}}}$

(20)

Type: Matrix(Expression(Integer))

fricas

map(Simplify, ω(S,R))

$\label{eq21}\left[ \begin{array}{c} 0 \ - s 1 \ - s 2 \ - s 3$

(21)

Type: Matrix(Expression(Integer))

fricas

map(Simplify, ω(U,V))

$\label{eq22}\left[ \begin{array}{c} {\frac{-{\cosh \left({{2 \ v}- u}\right)}+{\cosh \left({u}\right)}}{2 \ {\cosh \left({v - u}\right)}}} \ {\frac{-{\sinh \left({{2 \ v}- u}\right)}+{\sinh \left({u}\right)}}{2 \ {\cosh \left({v - u}\right)}}} \ 0 \ 0$

(22)

Type: Matrix(Expression(Integer))

Idempotent Observers

fricas

PP:=tensor(-P,P)

fricas

Compiling function tensor with type (Matrix(Expression(Integer)), 
      Matrix(Expression(Integer))) -> Matrix(Expression(Integer))

$\label{eq23}\left[ \begin{array}{cccc} {{p 0}^{2}}& -{p 0 \ p 1}& -{p 0 \ p 2}& -{p 0 \ p 3} \ {p 0 \ p 1}& -{{p 1}^{2}}& -{p 1 \ p 2}& -{p 1 \ p 3} \ {p 0 \ p 2}& -{p 1 \ p 2}& -{{p 2}^{2}}& -{p 2 \ p 3} \ {p 0 \ p 3}& -{p 1 \ p 3}& -{p 2 \ p 3}& -{{p 3}^{2}}$

(23)

Type: Matrix(Expression(Integer))

fricas

QQ:=tensor(-Q,Q);

Type: Matrix(Expression(Integer))

fricas

is?(trace(PP*QQ)=dot(P,Q)^2)

fricas

Compiling function is? with type Equation(Expression(Integer)) -> 
      Boolean

$\label{eq24} \mbox{\rm true}$

(24)

Type: Boolean

fricas

RR:=tensor(-R,R)

$\label{eq25}\left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0$

(25)

Type: Matrix(Expression(Integer))

fricas

SS:=map(Simplify,tensor(-S,S))

$\label{eq26}\left[ \begin{array}{cccc} -{\frac{1}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}}& -{\frac{s 1}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}}& -{\frac{s 2}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}}& -{\frac{s 3}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}} \ {\frac{s 1}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}}&{\frac{{s 1}^{2}}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}}&{\frac{s 1 \ s 2}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}}&{\frac{s 1 \ s 3}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}} \ {\frac{s 2}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}}&{\frac{s 1 \ s 2}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}}&{\frac{{s 2}^{2}}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}}&{\frac{s 2 \ s 3}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}} \ {\frac{s 3}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}}&{\frac{s 1 \ s 3}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}}&{\frac{s 2 \ s 3}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}}&{\frac{{s 3}^{2}}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}- 1}}$

(26)

Type: Matrix(Expression(Integer))

fricas

Is?(SS*SS=SS)

fricas

Compiling function Is? with type Equation(Matrix(Expression(Integer)
      )) -> Boolean

$\label{eq27} \mbox{\rm true}$

(27)

Type: Boolean

fricas

trace(SS)

$\label{eq28}1$

(28)

Type: Expression(Integer)

fricas

TT:=map(Simplify,tensor(-T,T));

Type: Matrix(Expression(Integer))

fricas

Is?(SS*TT*SS = dot(S,T)^2 * SS)

$\label{eq29} \mbox{\rm true}$

(29)

Type: Boolean

fricas

UU:=map(Simplify,tensor(-U,U))

$\label{eq30}\left[ \begin{array}{cccc} {\frac{{\cosh \left({2 \ u}\right)}+ 1}{2}}& -{\frac{\sinh \left({2 \ u}\right)}{2}}& 0 & 0 \ {\frac{\sinh \left({2 \ u}\right)}{2}}&{\frac{-{\cosh \left({2 \ u}\right)}+ 1}{2}}& 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0$

(30)

Type: Matrix(Expression(Integer))

fricas

VV:=map(Simplify,tensor(-V,V));

Type: Matrix(Expression(Integer))

fricas

map(Simplify, UU*VV)

$\label{eq31}\left[ \begin{array}{cccc} {\frac{{\cosh \left({2 \ v}\right)}+{\cosh \left({{2 \ v}-{2 \ u}}\right)}+{\cosh \left({2 \ u}\right)}+ 1}{4}}&{\frac{-{\sinh \left({2 \ v}\right)}-{\sinh \left({{2 \ v}-{2 \ u}}\right)}-{\sinh \left({2 \ u}\right)}}{4}}& 0 & 0 \ {\frac{{\sinh \left({2 \ v}\right)}-{\sinh \left({{2 \ v}-{2 \ u}}\right)}+{\sinh \left({2 \ u}\right)}}{4}}&{\frac{-{\cosh \left({2 \ v}\right)}+{\cosh \left({{2 \ v}-{2 \ u}}\right)}-{\cosh \left({2 \ u}\right)}+ 1}{4}}& 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0$

(31)

Type: Matrix(Expression(Integer))

fricas

WW:=map(Simplify,tensor(-W,W));

Type: Matrix(Expression(Integer))

fricas

Is?(SS*TT*WW = -dot(S,T)*dot(T,W)/dot(S,W)*SS*WW)

$\label{eq32} \mbox{\rm true}$

(32)

Type: Boolean

fricas

Is?(SS*TT*SS = dot(S,T)^2*SS)

$\label{eq33} \mbox{\rm true}$

(33)

Type: Boolean

Nilpotent Operators

fricas

AA:=tensor(-A,A)

$\label{eq34}\left[ \begin{array}{cccc} {{a 0}^{2}}& -{{{a 0}^{2}}\ a 1}& -{{{a 0}^{2}}\ a 2}& -{{{a 0}^{2}}\ {\sqrt{-{{a 2}^{2}}-{{a 1}^{2}}+ 1}}} \ {{{a 0}^{2}}\ a 1}& -{{{a 0}^{2}}\ {{a 1}^{2}}}& -{{{a 0}^{2}}\ a 1 \ a 2}& -{{{a 0}^{2}}\ a 1 \ {\sqrt{-{{a 2}^{2}}-{{a 1}^{2}}+ 1}}} \ {{{a 0}^{2}}\ a 2}& -{{{a 0}^{2}}\ a 1 \ a 2}& -{{{a 0}^{2}}\ {{a 2}^{2}}}& -{{{a 0}^{2}}\ a 2 \ {\sqrt{-{{a 2}^{2}}-{{a 1}^{2}}+ 1}}} \ {{{a 0}^{2}}\ {\sqrt{-{{a 2}^{2}}-{{a 1}^{2}}+ 1}}}& -{{{a 0}^{2}}\ a 1 \ {\sqrt{-{{a 2}^{2}}-{{a 1}^{2}}+ 1}}}& -{{{a 0}^{2}}\ a 2 \ {\sqrt{-{{a 2}^{2}}-{{a 1}^{2}}+ 1}}}&{{{{a 0}^{2}}\ {{a 2}^{2}}}+{{{a 0}^{2}}\ {{a 1}^{2}}}-{{a 0}^{2}}}$

(34)

Type: Matrix(Expression(Integer))

fricas

BB:=tensor(-B,B);

Type: Matrix(Expression(Integer))

fricas

CC:=tensor(-C,C);

Type: Matrix(Expression(Integer))

fricas

Is?(AA*AA=0*AA)

$\label{eq35} \mbox{\rm true}$

(35)

Type: Boolean

fricas

trace(AA)

$\label{eq36}0$

(36)

Type: Expression(Integer)

fricas

is?(trace(AA*BB)=dot(A,B)^2)

$\label{eq37} \mbox{\rm true}$

(37)

Type: Boolean

fricas

dot(A,B)

$\label{eq38}\begin{array}{@{}l} \displaystyle {a 0 \ b 0 \ {\sqrt{-{{b 2}^{2}}-{{b 1}^{2}}+ 1}}\ {\sqrt{-{{a 2}^{2}}-{{a 1}^{2}}+ 1}}}+{a 0 \ a 2 \ b 0 \ b 2}+ \ \ \displaystyle {a 0 \ a 1 \ b 0 \ b 1}-{a 0 \ b 0}$

(38)

Type: Expression(Integer)

fricas

possible(%)::Complex Float

fricas

Compiling function possible with type Expression(Integer) -> 
      Expression(Integer)

$\label{eq39}-{15364105.3285387906 \<u> 32}$

(39)

Type: Complex(Float)

fricas

Is?(AA*BB*CC = -dot(A,B)*dot(B,C)/dot(A,C)*AA*CC)

$\label{eq40} \mbox{\rm true}$

(40)

Type: Boolean

fricas

Is?(AA*BB*SS = -dot(A,B)*dot(B,S)/dot(A,S)*AA*SS)

$\label{eq41} \mbox{\rm true}$

(41)

Type: Boolean

fricas

Is?(AA*BB*SS=SS*AA*BB)

$\label{eq42} \mbox{\rm false}$

(42)

Type: Boolean

fricas

Is?(AA*BB*AA = dot(A,B)^2*AA)

$\label{eq43} \mbox{\rm true}$

(43)

Type: Boolean

Lie Bracket

fricas

STW:=(SS*TT-TT*SS)*WW;

Type: Matrix(Expression(Integer))

fricas

Is?(STW*STW=0*STW)

$\label{eq44} \mbox{\rm true}$

(44)

Type: Boolean

fricas

trace(STW)

$\label{eq45}0$

(45)

Type: Expression(Integer)

fricas

solve(map(x+->x=0,members(STW-AA)),[a0,a1,a2,a3])

$\label{eq46}\left[ \right]$

(46)

Type: List(List(Equation(Expression(Integer))))

fricas

ABC:=(AA*BB-BB*AA)*CC;

Type: Matrix(Expression(Integer))

fricas

Is?(ABC*ABC=0*ABC)

$\label{eq47} \mbox{\rm true}$

(47)

Type: Boolean

fricas

trace(ABC)

$\label{eq48}0$

(48)

Type: Expression(Integer)

fricas

PQR:=(PP*QQ-PP*QQ)*tensor(-vect([r0,r1,r2,r3]),vect([r0,r1,r2,r3]));

Type: Matrix(Expression(Integer))

fricas

Is?(PQR*PQR=0*PQR)

$\label{eq49} \mbox{\rm true}$

(49)

Type: Boolean

fricas

trace(PQR)

$\label{eq50}0$

(50)

Type: NonNegativeInteger?

fricas

map(Simplify,(PP*QQ-QQ*PP)*(PP*QQ-QQ*PP))

\label{eq51}\left[
\begin{array}{cccc}
{{{{p 0}^{2}}\ {{p 3}^{2}}\ {{q 3}^{4}}}+{{\left({2 \ {{p 0}^{2}}\ p 2 \ p 3 \ q 2}+{2 \ {{p 0}^{2}}\ p 1 \ p 3 \ q 1}+{{\left(-{2 \ p 0 \ {{p 3}^{3}}}-{2 \ {{p 0}^{3}}\ p 3}\right)}\ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left({{{p 0}^{2}}\ {{p 3}^{2}}}+{{{p 0}^{2}}\ {{p 2}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({2 \ {{p 0}^{2}}\ p 1 \ p 2 \ q 1}+{{\left(-{6 \ p 0 \ p 2 \ {{p 3}^{2}}}-{2 \ {{p 0}^{3}}\ p 2}\right)}\ q 0}\right)}\ q 2}+{{\left({{{p 0}^{2}}\ {{p 3}^{2}}}+{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 1}^{2}}}+{{\left(-{6 \ p 0 \ p 1 \ {{p 3}^{2}}}-{2 \ {{p 0}^{3}}\ p 1}\right)}\ q 0 \ q 1}+{{\left({{p 3}^{4}}+{{\left({{p 2}^{2}}+{{p 1}^{2}}+{4 \ {{p 0}^{2}}}\right)}\ {{p 3}^{2}}}+{{p 0}^{4}}\right)}\ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left({2 \ {{p 0}^{2}}\ p 2 \ p 3 \ {{q 2}^{3}}}+{{\left({2 \ {{p 0}^{2}}\ p 1 \ p 3 \ q 1}+{{\left(-{6 \ p 0 \ {{p 2}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 3 \ q 0}\right)}\ {{q 2}^{2}}}+{{\left({2 \ {{p 0}^{2}}\ p 2 \ p 3 \ {{q 1}^{2}}}-{{1
2}\ p 0 \ p 1 \ p 2 \ p 3 \ q 0 \ q 1}+{{\left({2 \ p 2 \ {{p 3}^{3}}}+{{\left({2 \ {{p 2}^{3}}}+{{\left({2 \ {{p 1}^{2}}}+{8 \ {{p 0}^{2}}}\right)}\ p 2}\right)}\ p 3}\right)}\ {{q 0}^{2}}}\right)}\ q 2}+{2 \ {{p 0}^{2}}\ p 1 \ p 3 \ {{q 1}^{3}}}+{{\left(-{6 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 3 \ q 0 \ {{q 1}^{2}}}+{{\left({2 \ p 1 \ {{p 3}^{3}}}+{{\left({2 \ p 1 \ {{p 2}^{2}}}+{2 \ {{p 1}^{3}}}+{8 \ {{p 0}^{2}}\ p 1}\right)}\ p 3}\right)}\ {{q 0}^{2}}\ q 1}+{{\left(-{2 \ p 0 \ {{p 3}^{3}}}+{{\left(-{2 \ p 0 \ {{p 2}^{2}}}-{2 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 3}\right)}\ {{q 0}^{3}}}\right)}\ q 3}+{{{p 0}^{2}}\ {{p 2}^{2}}\ {{q 2}^{4}}}+{{\left({2 \ {{p 0}^{2}}\ p 1 \ p 2 \ q 1}+{{\left(-{2 \ p 0 \ {{p 2}^{3}}}-{2 \ {{p 0}^{3}}\ p 2}\right)}\ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left({{{p 0}^{2}}\ {{p 2}^{2}}}+{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 1}^{2}}}+{{\left(-{6 \ p 0 \ p 1 \ {{p 2}^{2}}}-{2 \ {{p 0}^{3}}\ p 1}\right)}\ q 0 \ q 1}+{{\left({{{p 2}^{2}}\ {{p 3}^{2}}}+{{p 2}^{4}}+{{\left({{p 1}^{2}}+{4 \ {{p 0}^{2}}}\right)}\ {{p 2}^{2}}}+{{p 0}^{4}}\right)}\ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({2 \ {{p 0}^{2}}\ p 1 \ p 2 \ {{q 1}^{3}}}+{{\left(-{6 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 2 \ q 0 \ {{q 1}^{2}}}+{{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{2 \ p 1 \ {{p 2}^{3}}}+{{\left({2 \ {{p 1}^{3}}}+{8 \ {{p 0}^{2}}\ p 1}\right)}\ p 2}\right)}\ {{q 0}^{2}}\ q 1}+{{\left(-{2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{2 \ p 0 \ {{p 2}^{3}}}+{{\left(-{2 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 2}\right)}\ {{q 0}^{3}}}\right)}\ q 2}+{{{p 0}^{2}}\ {{p 1}^{2}}\ {{q 1}^{4}}}+{{\left(-{2 \ p 0 \ {{p 1}^{3}}}-{2 \ {{p 0}^{3}}\ p 1}\right)}\ q 0 \ {{q 1}^{3}}}+{{\left({{{p 1}^{2}}\ {{p 3}^{2}}}+{{{p 1}^{2}}\ {{p 2}^{2}}}+{{p 1}^{4}}+{4 \ {{p 0}^{2}}\ {{p 1}^{2}}}+{{p 0}^{4}}\right)}\ {{q 0}^{2}}\ {{q 1}^{2}}}+{{\left(-{2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{2 \ p 0 \ p 1 \ {{p 2}^{2}}}-{2 \ p 0 \ {{p 1}^{3}}}-{2 \ {{p 0}^{3}}\ p 1}\right)}\ {{q 0}^{3}}\ q 1}+{{\left({{{p 0}^{2}}\ {{p 3}^{2}}}+{{{p 0}^{2}}\ {{p 2}^{2}}}+{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 0}^{4}}}}&{-{p 0 \ p 1 \ {{p 3}^{2}}\ {{q 3}^{4}}}+{{\left(-{2 \ p 0 \ p 1 \ p 2 \ p 3 \ q 2}+{{\left({p 0 \ {{p 3}^{3}}}-{2 \ p 0 \ {{p 1}^{2}}\ p 3}\right)}\ q 1}+{{\left({p 1 \ {{p 3}^{3}}}+{2 \ {{p 0}^{2}}\ p 1 \ p 3}\right)}\ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left(-{p 0 \ p 1 \ {{p 3}^{2}}}-{p 0 \ p 1 \ {{p 2}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left({3 \ p 0 \ p 2 \ {{p 3}^{2}}}-{2 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ q 1}+{{\left({3 \ p 1 \ p 2 \ {{p 3}^{2}}}+{2 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ q 0}\right)}\ q 2}+{{\left({2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{p 0 \ {{p 1}^{3}}}\right)}\ {{q 1}^{2}}}+{{\left(-{{p 3}^{4}}+{{\left(-{{p 2}^{2}}+{2 \ {{p 1}^{2}}}-{2 \ {{p 0}^{2}}}\right)}\ {{p 3}^{2}}}+{2 \ {{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ q 0 \ q 1}+{{\left(-{2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{{{p 0}^{3}}\ p 1}\right)}\ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left(-{2 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 2}^{3}}}+{{\left({{\left({3 \ p 0 \ {{p 2}^{2}}}-{2 \ p 0 \ {{p 1}^{2}}}\right)}\ p 3 \ q 1}+{{\left({3 \ p 1 \ {{p 2}^{2}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ q 0}\right)}\ {{q 2}^{2}}}+{{\left({4 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 1}^{2}}}+{{\left(-{2 \ p 2 \ {{p 3}^{3}}}+{{\left(-{2 \ {{p 2}^{3}}}+{{\left({4 \ {{p 1}^{2}}}-{4 \ {{p 0}^{2}}}\right)}\ p 2}\right)}\ p 3}\right)}\ q 0 \ q 1}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 0}^{2}}}\right)}\ q 2}+{p 0 \ {{p 1}^{2}}\ p 3 \ {{q 1}^{3}}}+{{\left(-{2 \ p 1 \ {{p 3}^{3}}}+{{\left(-{2 \ p 1 \ {{p 2}^{2}}}+{{p 1}^{3}}-{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left({2 \ p 0 \ {{p 3}^{3}}}+{{\left({2 \ p 0 \ {{p 2}^{2}}}-{2 \ p 0 \ {{p 1}^{2}}}+{{p 0}^{3}}\right)}\ p 3}\right)}\ {{q 0}^{2}}\ q 1}+{{{p 0}^{2}}\ p 1 \ p 3 \ {{q 0}^{3}}}\right)}\ q 3}-{p 0 \ p 1 \ {{p 2}^{2}}\ {{q 2}^{4}}}+{{\left({{\left({p 0 \ {{p 2}^{3}}}-{2 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ q 1}+{{\left({p 1 \ {{p 2}^{3}}}+{2 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left({2 \ p 0 \ p 1 \ {{p 2}^{2}}}-{p 0 \ {{p 1}^{3}}}\right)}\ {{q 1}^{2}}}+{{\left(-{{{p 2}^{2}}\ {{p 3}^{2}}}-{{p 2}^{4}}+{{\left({2 \ {{p 1}^{2}}}-{2 \ {{p 0}^{2}}}\right)}\ {{p 2}^{2}}}+{2 \ {{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ q 0 \ q 1}+{{\left(-{2 \ p 0 \ p 1 \ {{p 2}^{2}}}-{{{p 0}^{3}}\ p 1}\right)}\ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({p 0 \ {{p 1}^{2}}\ p 2 \ {{q 1}^{3}}}+{{\left(-{2 \ p 1 \ p 2 \ {{p 3}^{2}}}-{2 \ p 1 \ {{p 2}^{3}}}+{{\left({{p 1}^{3}}-{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left({2 \ p 0 \ p 2 \ {{p 3}^{2}}}+{2 \ p 0 \ {{p 2}^{3}}}+{{\left(-{2 \ p 0 \ {{p 1}^{2}}}+{{p 0}^{3}}\right)}\ p 2}\right)}\ {{q 0}^{2}}\ q 1}+{{{p 0}^{2}}\ p 1 \ p 2 \ {{q 0}^{3}}}\right)}\ q 2}+{{\left(-{{{p 1}^{2}}\ {{p 3}^{2}}}-{{{p 1}^{2}}\ {{p 2}^{2}}}\right)}\ q 0 \ {{q 1}^{3}}}+{{\left({2 \ p 0 \ p 1 \ {{p 3}^{2}}}+{2 \ p 0 \ p 1 \ {{p 2}^{2}}}\right)}\ {{q 0}^{2}}\ {{q 1}^{2}}}+{{\left(-{{{p 0}^{2}}\ {{p 3}^{2}}}-{{{p 0}^{2}}\ {{p 2}^{2}}}\right)}\ {{q 0}^{3}}\ q 1}}&{-{p 0 \ p 2 \ {{p 3}^{2}}\ {{q 3}^{4}}}+{{\left({{\left({p 0 \ {{p 3}^{3}}}-{2 \ p 0 \ {{p 2}^{2}}\ p 3}\right)}\ q 2}-{2 \ p 0 \ p 1 \ p 2 \ p 3 \ q 1}+{{\left({p 2 \ {{p 3}^{3}}}+{2 \ {{p 0}^{2}}\ p 2 \ p 3}\right)}\ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left({2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{p 0 \ {{p 2}^{3}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left({3 \ p 0 \ p 1 \ {{p 3}^{2}}}-{2 \ p 0 \ p 1 \ {{p 2}^{2}}}\right)}\ q 1}+{{\left(-{{p 3}^{4}}+{{\left({2 \ {{p 2}^{2}}}-{{p 1}^{2}}-{2 \ {{p 0}^{2}}}\right)}\ {{p 3}^{2}}}+{2 \ {{p 0}^{2}}\ {{p 2}^{2}}}\right)}\ q 0}\right)}\ q 2}+{{\left(-{p 0 \ p 2 \ {{p 3}^{2}}}-{p 0 \ {{p 1}^{2}}\ p 2}\right)}\ {{q 1}^{2}}}+{{\left({3 \ p 1 \ p 2 \ {{p 3}^{2}}}+{2 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ q 0 \ q 1}+{{\left(-{2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{{{p 0}^{3}}\ p 2}\right)}\ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left({p 0 \ {{p 2}^{2}}\ p 3 \ {{q 2}^{3}}}+{{\left({4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 1}+{{\left(-{2 \ p 2 \ {{p 3}^{3}}}+{{\left({{p 2}^{3}}+{{\left(-{2 \ {{p 1}^{2}}}-{2 \ {{p 0}^{2}}}\right)}\ p 2}\right)}\ p 3}\right)}\ q 0}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{2 \ p 0 \ {{p 2}^{2}}}+{3 \ p 0 \ {{p 1}^{2}}}\right)}\ p 3 \ {{q 1}^{2}}}+{{\left(-{2 \ p 1 \ {{p 3}^{3}}}+{{\left({4 \ p 1 \ {{p 2}^{2}}}-{2 \ {{p 1}^{3}}}-{4 \ {{p 0}^{2}}\ p 1}\right)}\ p 3}\right)}\ q 0 \ q 1}+{{\left({2 \ p 0 \ {{p 3}^{3}}}+{{\left(-{2 \ p 0 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{2}}}+{{p 0}^{3}}\right)}\ p 3}\right)}\ {{q 0}^{2}}}\right)}\ q 2}-{2 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 1}^{3}}}+{{\left({3 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ p 2 \ p 3 \ q 0 \ {{q 1}^{2}}}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 0}^{2}}\ q 1}+{{{p 0}^{2}}\ p 2 \ p 3 \ {{q 0}^{3}}}\right)}\ q 3}+{{\left({p 0 \ p 1 \ {{p 2}^{2}}\ q 1}+{{\left(-{{{p 2}^{2}}\ {{p 3}^{2}}}-{{{p 1}^{2}}\ {{p 2}^{2}}}\right)}\ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left(-{p 0 \ {{p 2}^{3}}}+{2 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ {{q 1}^{2}}}+{{\left(-{2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{p 1 \ {{p 2}^{3}}}+{{\left(-{2 \ {{p 1}^{3}}}-{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2}\right)}\ q 0 \ q 1}+{{\left({2 \ p 0 \ p 2 \ {{p 3}^{2}}}+{2 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{2 \ p 0 \ p 1 \ {{p 2}^{2}}}+{p 0 \ {{p 1}^{3}}}\right)}\ {{q 1}^{3}}}+{{\left(-{{{p 1}^{2}}\ {{p 3}^{2}}}+{{\left({2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ {{p 2}^{2}}}-{{p 1}^{4}}-{2 \ {{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left({2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{2 \ p 0 \ p 1 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{3}}}+{{{p 0}^{3}}\ p 1}\right)}\ {{q 0}^{2}}\ q 1}+{{\left(-{{{p 0}^{2}}\ {{p 3}^{2}}}-{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 0}^{3}}}\right)}\ q 2}-{p 0 \ {{p 1}^{2}}\ p 2 \ {{q 1}^{4}}}+{{\left({{p 1}^{3}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2 \ q 0 \ {{q 1}^{3}}}+{{\left(-{2 \ p 0 \ {{p 1}^{2}}}-{{p 0}^{3}}\right)}\ p 2 \ {{q 0}^{2}}\ {{q 1}^{2}}}+{{{p 0}^{2}}\ p 1 \ p 2 \ {{q 0}^{3}}\ q 1}}&{{{\left({p 0 \ p 2 \ {{p 3}^{2}}\ q 2}+{p 0 \ p 1 \ {{p 3}^{2}}\ q 1}+{{\left(-{{p 2}^{2}}-{{p 1}^{2}}\right)}\ {{p 3}^{2}}\ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left(-{p 0 \ {{p 3}^{3}}}+{2 \ p 0 \ {{p 2}^{2}}\ p 3}\right)}\ {{q 2}^{2}}}+{{\left({4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 1}+{{\left({p 2 \ {{p 3}^{3}}}+{{\left(-{2 \ {{p 2}^{3}}}+{{\left(-{2 \ {{p 1}^{2}}}-{2 \ {{p 0}^{2}}}\right)}\ p 2}\right)}\ p 3}\right)}\ q 0}\right)}\ q 2}+{{\left(-{p 0 \ {{p 3}^{3}}}+{2 \ p 0 \ {{p 1}^{2}}\ p 3}\right)}\ {{q 1}^{2}}}+{{\left({p 1 \ {{p 3}^{3}}}+{{\left(-{2 \ p 1 \ {{p 2}^{2}}}-{2 \ {{p 1}^{3}}}-{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3}\right)}\ q 0 \ q 1}+{{\left({2 \ p 0 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{2}}}\right)}\ p 3 \ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left({{\left(-{2 \ p 0 \ p 2 \ {{p 3}^{2}}}+{p 0 \ {{p 2}^{3}}}\right)}\ {{q 2}^{3}}}+{{\left({{\left(-{2 \ p 0 \ p 1 \ {{p 3}^{2}}}+{3 \ p 0 \ p 1 \ {{p 2}^{2}}}\right)}\ q 1}+{{\left({{\left({2 \ {{p 2}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ {{p 3}^{2}}}-{{p 2}^{4}}+{{\left(-{{p 1}^{2}}-{2 \ {{p 0}^{2}}}\right)}\ {{p 2}^{2}}}\right)}\ q 0}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{2 \ p 0 \ p 2 \ {{p 3}^{2}}}+{3 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ {{q 1}^{2}}}+{{\left({4 \ p 1 \ p 2 \ {{p 3}^{2}}}-{2 \ p 1 \ {{p 2}^{3}}}+{{\left(-{2 \ {{p 1}^{3}}}-{4 \ {{p 0}^{2}}\ p 1}\right)}\ p 2}\right)}\ q 0 \ q 1}+{{\left(-{2 \ p 0 \ p 2 \ {{p 3}^{2}}}+{2 \ p 0 \ {{p 2}^{3}}}+{{\left({2 \ p 0 \ {{p 1}^{2}}}+{{p 0}^{3}}\right)}\ p 2}\right)}\ {{q 0}^{2}}}\right)}\ q 2}+{{\left(-{2 \ p 0 \ p 1 \ {{p 3}^{2}}}+{p 0 \ {{p 1}^{3}}}\right)}\ {{q 1}^{3}}}+{{\left({{\left({2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ {{p 3}^{2}}}-{{{p 1}^{2}}\ {{p 2}^{2}}}-{{p 1}^{4}}-{2 \ {{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left(-{2 \ p 0 \ p 1 \ {{p 3}^{2}}}+{2 \ p 0 \ p 1 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{3}}}+{{{p 0}^{3}}\ p 1}\right)}\ {{q 0}^{2}}\ q 1}+{{\left(-{{{p 0}^{2}}\ {{p 2}^{2}}}-{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 0}^{3}}}\right)}\ q 3}-{p 0 \ {{p 2}^{2}}\ p 3 \ {{q 2}^{4}}}+{{\left(-{2 \ p 0 \ p 1 \ p 2 \ p 3 \ q 1}+{{\left({{p 2}^{3}}+{2 \ {{p 0}^{2}}\ p 2}\right)}\ p 3 \ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left(-{p 0 \ {{p 2}^{2}}}-{p 0 \ {{p 1}^{2}}}\right)}\ p 3 \ {{q 1}^{2}}}+{{\left({3 \ p 1 \ {{p 2}^{2}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ q 0 \ q 1}+{{\left(-{2 \ p 0 \ {{p 2}^{2}}}-{{p 0}^{3}}\right)}\ p 3 \ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left(-{2 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 1}^{3}}}+{{\left({3 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ p 2 \ p 3 \ q 0 \ {{q 1}^{2}}}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 0}^{2}}\ q 1}+{{{p 0}^{2}}\ p 2 \ p 3 \ {{q 0}^{3}}}\right)}\ q 2}-{p 0 \ {{p 1}^{2}}\ p 3 \ {{q 1}^{4}}}+{{\left({{p 1}^{3}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ q 0 \ {{q 1}^{3}}}+{{\left(-{2 \ p 0 \ {{p 1}^{2}}}-{{p 0}^{3}}\right)}\ p 3 \ {{q 0}^{2}}\ {{q 1}^{2}}}+{{{p 0}^{2}}\ p 1 \ p 3 \ {{q 0}^{3}}\ q 1}}
\
{{p 0 \ p 1 \ {{p 3}^{2}}\ {{q 3}^{4}}}+{{\left({2 \ p 0 \ p 1 \ p 2 \ p 3 \ q 2}+{{\left(-{p 0 \ {{p 3}^{3}}}+{2 \ p 0 \ {{p 1}^{2}}\ p 3}\right)}\ q 1}+{{\left(-{p 1 \ {{p 3}^{3}}}-{2 \ {{p 0}^{2}}\ p 1 \ p 3}\right)}\ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left({p 0 \ p 1 \ {{p 3}^{2}}}+{p 0 \ p 1 \ {{p 2}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{3 \ p 0 \ p 2 \ {{p 3}^{2}}}+{2 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ q 1}+{{\left(-{3 \ p 1 \ p 2 \ {{p 3}^{2}}}-{2 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ q 0}\right)}\ q 2}+{{\left(-{2 \ p 0 \ p 1 \ {{p 3}^{2}}}+{p 0 \ {{p 1}^{3}}}\right)}\ {{q 1}^{2}}}+{{\left({{p 3}^{4}}+{{\left({{p 2}^{2}}-{2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ {{p 3}^{2}}}-{2 \ {{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ q 0 \ q 1}+{{\left({2 \ p 0 \ p 1 \ {{p 3}^{2}}}+{{{p 0}^{3}}\ p 1}\right)}\ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left({2 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 2}^{3}}}+{{\left({{\left(-{3 \ p 0 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{2}}}\right)}\ p 3 \ q 1}+{{\left(-{3 \ p 1 \ {{p 2}^{2}}}-{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ q 0}\right)}\ {{q 2}^{2}}}+{{\left(-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 1}^{2}}}+{{\left({2 \ p 2 \ {{p 3}^{3}}}+{{\left({2 \ {{p 2}^{3}}}+{{\left(-{4 \ {{p 1}^{2}}}+{4 \ {{p 0}^{2}}}\right)}\ p 2}\right)}\ p 3}\right)}\ q 0 \ q 1}+{4 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 0}^{2}}}\right)}\ q 2}-{p 0 \ {{p 1}^{2}}\ p 3 \ {{q 1}^{3}}}+{{\left({2 \ p 1 \ {{p 3}^{3}}}+{{\left({2 \ p 1 \ {{p 2}^{2}}}-{{p 1}^{3}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left(-{2 \ p 0 \ {{p 3}^{3}}}+{{\left(-{2 \ p 0 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{2}}}-{{p 0}^{3}}\right)}\ p 3}\right)}\ {{q 0}^{2}}\ q 1}-{{{p 0}^{2}}\ p 1 \ p 3 \ {{q 0}^{3}}}\right)}\ q 3}+{p 0 \ p 1 \ {{p 2}^{2}}\ {{q 2}^{4}}}+{{\left({{\left(-{p 0 \ {{p 2}^{3}}}+{2 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ q 1}+{{\left(-{p 1 \ {{p 2}^{3}}}-{2 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left(-{2 \ p 0 \ p 1 \ {{p 2}^{2}}}+{p 0 \ {{p 1}^{3}}}\right)}\ {{q 1}^{2}}}+{{\left({{{p 2}^{2}}\ {{p 3}^{2}}}+{{p 2}^{4}}+{{\left(-{2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ {{p 2}^{2}}}-{2 \ {{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ q 0 \ q 1}+{{\left({2 \ p 0 \ p 1 \ {{p 2}^{2}}}+{{{p 0}^{3}}\ p 1}\right)}\ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left(-{p 0 \ {{p 1}^{2}}\ p 2 \ {{q 1}^{3}}}+{{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{2 \ p 1 \ {{p 2}^{3}}}+{{\left(-{{p 1}^{3}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left(-{2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{2 \ p 0 \ {{p 2}^{3}}}+{{\left({2 \ p 0 \ {{p 1}^{2}}}-{{p 0}^{3}}\right)}\ p 2}\right)}\ {{q 0}^{2}}\ q 1}-{{{p 0}^{2}}\ p 1 \ p 2 \ {{q 0}^{3}}}\right)}\ q 2}+{{\left({{{p 1}^{2}}\ {{p 3}^{2}}}+{{{p 1}^{2}}\ {{p 2}^{2}}}\right)}\ q 0 \ {{q 1}^{3}}}+{{\left(-{2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{2 \ p 0 \ p 1 \ {{p 2}^{2}}}\right)}\ {{q 0}^{2}}\ {{q 1}^{2}}}+{{\left({{{p 0}^{2}}\ {{p 3}^{2}}}+{{{p 0}^{2}}\ {{p 2}^{2}}}\right)}\ {{q 0}^{3}}\ q 1}}&{-{{{p 1}^{2}}\ {{p 3}^{2}}\ {{q 3}^{4}}}+{{\left(-{2 \ {{p 1}^{2}}\ p 2 \ p 3 \ q 2}+{{\left({2 \ p 1 \ {{p 3}^{3}}}-{2 \ {{p 1}^{3}}\ p 3}\right)}\ q 1}+{2 \ p 0 \ {{p 1}^{2}}\ p 3 \ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left(-{{{p 1}^{2}}\ {{p 3}^{2}}}-{{{p 1}^{2}}\ {{p 2}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left({6 \ p 1 \ p 2 \ {{p 3}^{2}}}-{2 \ {{p 1}^{3}}\ p 2}\right)}\ q 1}+{2 \ p 0 \ {{p 1}^{2}}\ p 2 \ q 0}\right)}\ q 2}+{{\left(-{{p 3}^{4}}+{{\left(-{{p 2}^{2}}+{4 \ {{p 1}^{2}}}+{{p 0}^{2}}\right)}\ {{p 3}^{2}}}-{{p 1}^{4}}\right)}\ {{q 1}^{2}}}+{{\left(-{6 \ p 0 \ p 1 \ {{p 3}^{2}}}+{2 \ p 0 \ {{p 1}^{3}}}\right)}\ q 0 \ q 1}+{{\left({{{p 1}^{2}}\ {{p 3}^{2}}}-{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left(-{2 \ {{p 1}^{2}}\ p 2 \ p 3 \ {{q 2}^{3}}}+{{\left({{\left({6 \ p 1 \ {{p 2}^{2}}}-{2 \ {{p 1}^{3}}}\right)}\ p 3 \ q 1}+{2 \ p 0 \ {{p 1}^{2}}\ p 3 \ q 0}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{2 \ p 2 \ {{p 3}^{3}}}+{{\left(-{2 \ {{p 2}^{3}}}+{{\left({8 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ p 2}\right)}\ p 3}\right)}\ {{q 1}^{2}}}-{{12}\ p 0 \ p 1 \ p 2 \ p 3 \ q 0 \ q 1}+{2 \ {{p 1}^{2}}\ p 2 \ p 3 \ {{q 0}^{2}}}\right)}\ q 2}+{{\left(-{2 \ p 1 \ {{p 3}^{3}}}+{{\left(-{2 \ p 1 \ {{p 2}^{2}}}+{2 \ {{p 1}^{3}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3}\right)}\ {{q 1}^{3}}}+{{\left({2 \ p 0 \ {{p 3}^{3}}}+{{\left({2 \ p 0 \ {{p 2}^{2}}}-{8 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 3}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left({2 \ {{p 1}^{3}}}+{6 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ {{q 0}^{2}}\ q 1}-{2 \ p 0 \ {{p 1}^{2}}\ p 3 \ {{q 0}^{3}}}\right)}\ q 3}-{{{p 1}^{2}}\ {{p 2}^{2}}\ {{q 2}^{4}}}+{{\left({{\left({2 \ p 1 \ {{p 2}^{3}}}-{2 \ {{p 1}^{3}}\ p 2}\right)}\ q 1}+{2 \ p 0 \ {{p 1}^{2}}\ p 2 \ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left(-{{{p 2}^{2}}\ {{p 3}^{2}}}-{{p 2}^{4}}+{{\left({4 \ {{p 1}^{2}}}+{{p 0}^{2}}\right)}\ {{p 2}^{2}}}-{{p 1}^{4}}\right)}\ {{q 1}^{2}}}+{{\left(-{6 \ p 0 \ p 1 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{3}}}\right)}\ q 0 \ q 1}+{{\left({{{p 1}^{2}}\ {{p 2}^{2}}}-{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{2 \ p 1 \ p 2 \ {{p 3}^{2}}}-{2 \ p 1 \ {{p 2}^{3}}}+{{\left({2 \ {{p 1}^{3}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2}\right)}\ {{q 1}^{3}}}+{{\left({2 \ p 0 \ p 2 \ {{p 3}^{2}}}+{2 \ p 0 \ {{p 2}^{3}}}+{{\left(-{8 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 2}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left({2 \ {{p 1}^{3}}}+{6 \ {{p 0}^{2}}\ p 1}\right)}\ p 2 \ {{q 0}^{2}}\ q 1}-{2 \ p 0 \ {{p 1}^{2}}\ p 2 \ {{q 0}^{3}}}\right)}\ q 2}+{{\left(-{{{p 1}^{2}}\ {{p 3}^{2}}}-{{{p 1}^{2}}\ {{p 2}^{2}}}+{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 1}^{4}}}+{{\left({2 \ p 0 \ p 1 \ {{p 3}^{2}}}+{2 \ p 0 \ p 1 \ {{p 2}^{2}}}-{2 \ p 0 \ {{p 1}^{3}}}-{2 \ {{p 0}^{3}}\ p 1}\right)}\ q 0 \ {{q 1}^{3}}}+{{\left(-{{{p 0}^{2}}\ {{p 3}^{2}}}-{{{p 0}^{2}}\ {{p 2}^{2}}}+{{p 1}^{4}}+{4 \ {{p 0}^{2}}\ {{p 1}^{2}}}+{{p 0}^{4}}\right)}\ {{q 0}^{2}}\ {{q 1}^{2}}}+{{\left(-{2 \ p 0 \ {{p 1}^{3}}}-{2 \ {{p 0}^{3}}\ p 1}\right)}\ {{q 0}^{3}}\ q 1}+{{{p 0}^{2}}\ {{p 1}^{2}}\ {{q 0}^{4}}}}&{-{p 1 \ p 2 \ {{p 3}^{2}}\ {{q 3}^{4}}}+{{\left({{\left({p 1 \ {{p 3}^{3}}}-{2 \ p 1 \ {{p 2}^{2}}\ p 3}\right)}\ q 2}+{{\left({p 2 \ {{p 3}^{3}}}-{2 \ {{p 1}^{2}}\ p 2 \ p 3}\right)}\ q 1}+{2 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}-{p 1 \ {{p 2}^{3}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{{p 3}^{4}}+{{\left({2 \ {{p 2}^{2}}}+{2 \ {{p 1}^{2}}}+{{p 0}^{2}}\right)}\ {{p 3}^{2}}}-{2 \ {{p 1}^{2}}\ {{p 2}^{2}}}\right)}\ q 1}+{{\left(-{3 \ p 0 \ p 1 \ {{p 3}^{2}}}+{2 \ p 0 \ p 1 \ {{p 2}^{2}}}\right)}\ q 0}\right)}\ q 2}+{{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}-{{{p 1}^{3}}\ p 2}\right)}\ {{q 1}^{2}}}+{{\left(-{3 \ p 0 \ p 2 \ {{p 3}^{2}}}+{2 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ q 0 \ q 1}+{{\left({p 1 \ p 2 \ {{p 3}^{2}}}-{{{p 0}^{2}}\ p 1 \ p 2}\right)}\ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left({p 1 \ {{p 2}^{2}}\ p 3 \ {{q 2}^{3}}}+{{\left({{\left(-{2 \ p 2 \ {{p 3}^{3}}}+{{\left({{p 2}^{3}}+{{\left({2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ p 2}\right)}\ p 3}\right)}\ q 1}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{2 \ p 1 \ {{p 3}^{3}}}+{{\left({2 \ p 1 \ {{p 2}^{2}}}+{{p 1}^{3}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3}\right)}\ {{q 1}^{2}}}+{{\left({2 \ p 0 \ {{p 3}^{3}}}+{{\left(-{4 \ p 0 \ {{p 2}^{2}}}-{4 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 3}\right)}\ q 0 \ q 1}+{{\left({2 \ p 1 \ {{p 2}^{2}}}+{3 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ {{q 0}^{2}}}\right)}\ q 2}+{{{p 1}^{2}}\ p 2 \ p 3 \ {{q 1}^{3}}}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0 \ {{q 1}^{2}}}+{{\left({2 \ {{p 1}^{2}}}+{3 \ {{p 0}^{2}}}\right)}\ p 2 \ p 3 \ {{q 0}^{2}}\ q 1}-{2 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 0}^{3}}}\right)}\ q 3}+{{\left({{\left(-{{{p 2}^{2}}\ {{p 3}^{2}}}+{{{p 0}^{2}}\ {{p 2}^{2}}}\right)}\ q 1}-{p 0 \ p 1 \ {{p 2}^{2}}\ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left(-{2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{2 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ {{q 1}^{2}}}+{{\left({2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{p 0 \ {{p 2}^{3}}}+{{\left(-{2 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 2}\right)}\ q 0 \ q 1}+{{\left({p 1 \ {{p 2}^{3}}}+{2 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{{{p 1}^{2}}\ {{p 3}^{2}}}+{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 1}^{3}}}+{{\left({2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{2 \ p 0 \ p 1 \ {{p 2}^{2}}}-{p 0 \ {{p 1}^{3}}}-{2 \ {{p 0}^{3}}\ p 1}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left(-{{{p 0}^{2}}\ {{p 3}^{2}}}+{{\left({2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ {{p 2}^{2}}}+{2 \ {{p 0}^{2}}\ {{p 1}^{2}}}+{{p 0}^{4}}\right)}\ {{q 0}^{2}}\ q 1}+{{\left(-{2 \ p 0 \ p 1 \ {{p 2}^{2}}}-{{{p 0}^{3}}\ p 1}\right)}\ {{q 0}^{3}}}\right)}\ q 2}-{p 0 \ {{p 1}^{2}}\ p 2 \ q 0 \ {{q 1}^{3}}}+{{\left({{p 1}^{3}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2 \ {{q 0}^{2}}\ {{q 1}^{2}}}+{{\left(-{2 \ p 0 \ {{p 1}^{2}}}-{{p 0}^{3}}\right)}\ p 2 \ {{q 0}^{3}}\ q 1}+{{{p 0}^{2}}\ p 1 \ p 2 \ {{q 0}^{4}}}}&{{{\left({p 1 \ p 2 \ {{p 3}^{2}}\ q 2}+{{\left(-{{p 2}^{2}}+{{p 0}^{2}}\right)}\ {{p 3}^{2}}\ q 1}-{p 0 \ p 1 \ {{p 3}^{2}}\ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left(-{p 1 \ {{p 3}^{3}}}+{2 \ p 1 \ {{p 2}^{2}}\ p 3}\right)}\ {{q 2}^{2}}}+{{\left({{\left({p 2 \ {{p 3}^{3}}}+{{\left(-{2 \ {{p 2}^{3}}}+{{\left({2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ p 2}\right)}\ p 3}\right)}\ q 1}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0}\right)}\ q 2}+{{\left(-{2 \ p 1 \ {{p 2}^{2}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ {{q 1}^{2}}}+{{\left(-{p 0 \ {{p 3}^{3}}}+{{\left({2 \ p 0 \ {{p 2}^{2}}}-{2 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 3}\right)}\ q 0 \ q 1}+{{\left({p 1 \ {{p 3}^{3}}}+{2 \ {{p 0}^{2}}\ p 1 \ p 3}\right)}\ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left({{\left(-{2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{p 1 \ {{p 2}^{3}}}\right)}\ {{q 2}^{3}}}+{{\left({{\left({{\left({2 \ {{p 2}^{2}}}-{2 \ {{p 1}^{2}}}\right)}\ {{p 3}^{2}}}-{{p 2}^{4}}+{{\left({2 \ {{p 1}^{2}}}+{{p 0}^{2}}\right)}\ {{p 2}^{2}}}\right)}\ q 1}+{{\left({2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{3 \ p 0 \ p 1 \ {{p 2}^{2}}}\right)}\ q 0}\right)}\ {{q 2}^{2}}}+{{\left({{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}-{2 \ p 1 \ {{p 2}^{3}}}+{{\left({{p 1}^{3}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2}\right)}\ {{q 1}^{2}}}+{{\left(-{4 \ p 0 \ p 2 \ {{p 3}^{2}}}+{2 \ p 0 \ {{p 2}^{3}}}+{{\left(-{4 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 2}\right)}\ q 0 \ q 1}+{{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{3 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ {{q 0}^{2}}}\right)}\ q 2}+{{\left(-{{{p 1}^{2}}\ {{p 2}^{2}}}+{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 1}^{3}}}+{{\left(-{2 \ p 0 \ p 1 \ {{p 3}^{2}}}+{2 \ p 0 \ p 1 \ {{p 2}^{2}}}-{p 0 \ {{p 1}^{3}}}-{2 \ {{p 0}^{3}}\ p 1}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left({{\left({2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ {{p 3}^{2}}}-{{{p 0}^{2}}\ {{p 2}^{2}}}+{2 \ {{p 0}^{2}}\ {{p 1}^{2}}}+{{p 0}^{4}}\right)}\ {{q 0}^{2}}\ q 1}+{{\left(-{2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{{{p 0}^{3}}\ p 1}\right)}\ {{q 0}^{3}}}\right)}\ q 3}-{p 1 \ {{p 2}^{2}}\ p 3 \ {{q 2}^{4}}}+{{\left({{\left({{p 2}^{3}}-{2 \ {{p 1}^{2}}\ p 2}\right)}\ p 3 \ q 1}+{2 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left({2 \ p 1 \ {{p 2}^{2}}}-{{p 1}^{3}}\right)}\ p 3 \ {{q 1}^{2}}}+{{\left(-{3 \ p 0 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{2}}}\right)}\ p 3 \ q 0 \ q 1}+{{\left({p 1 \ {{p 2}^{2}}}-{{{p 0}^{2}}\ p 1}\right)}\ p 3 \ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({{{p 1}^{2}}\ p 2 \ p 3 \ {{q 1}^{3}}}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0 \ {{q 1}^{2}}}+{{\left({2 \ {{p 1}^{2}}}+{3 \ {{p 0}^{2}}}\right)}\ p 2 \ p 3 \ {{q 0}^{2}}\ q 1}-{2 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 0}^{3}}}\right)}\ q 2}-{p 0 \ {{p 1}^{2}}\ p 3 \ q 0 \ {{q 1}^{3}}}+{{\left({{p 1}^{3}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ {{q 0}^{2}}\ {{q 1}^{2}}}+{{\left(-{2 \ p 0 \ {{p 1}^{2}}}-{{p 0}^{3}}\right)}\ p 3 \ {{q 0}^{3}}\ q 1}+{{{p 0}^{2}}\ p 1 \ p 3 \ {{q 0}^{4}}}}
\
{{p 0 \ p 2 \ {{p 3}^{2}}\ {{q 3}^{4}}}+{{\left({{\left(-{p 0 \ {{p 3}^{3}}}+{2 \ p 0 \ {{p 2}^{2}}\ p 3}\right)}\ q 2}+{2 \ p 0 \ p 1 \ p 2 \ p 3 \ q 1}+{{\left(-{p 2 \ {{p 3}^{3}}}-{2 \ {{p 0}^{2}}\ p 2 \ p 3}\right)}\ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left(-{2 \ p 0 \ p 2 \ {{p 3}^{2}}}+{p 0 \ {{p 2}^{3}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{3 \ p 0 \ p 1 \ {{p 3}^{2}}}+{2 \ p 0 \ p 1 \ {{p 2}^{2}}}\right)}\ q 1}+{{\left({{p 3}^{4}}+{{\left(-{2 \ {{p 2}^{2}}}+{{p 1}^{2}}+{2 \ {{p 0}^{2}}}\right)}\ {{p 3}^{2}}}-{2 \ {{p 0}^{2}}\ {{p 2}^{2}}}\right)}\ q 0}\right)}\ q 2}+{{\left({p 0 \ p 2 \ {{p 3}^{2}}}+{p 0 \ {{p 1}^{2}}\ p 2}\right)}\ {{q 1}^{2}}}+{{\left(-{3 \ p 1 \ p 2 \ {{p 3}^{2}}}-{2 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ q 0 \ q 1}+{{\left({2 \ p 0 \ p 2 \ {{p 3}^{2}}}+{{{p 0}^{3}}\ p 2}\right)}\ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left(-{p 0 \ {{p 2}^{2}}\ p 3 \ {{q 2}^{3}}}+{{\left(-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 1}+{{\left({2 \ p 2 \ {{p 3}^{3}}}+{{\left(-{{p 2}^{3}}+{{\left({2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ p 2}\right)}\ p 3}\right)}\ q 0}\right)}\ {{q 2}^{2}}}+{{\left({{\left({2 \ p 0 \ {{p 2}^{2}}}-{3 \ p 0 \ {{p 1}^{2}}}\right)}\ p 3 \ {{q 1}^{2}}}+{{\left({2 \ p 1 \ {{p 3}^{3}}}+{{\left(-{4 \ p 1 \ {{p 2}^{2}}}+{2 \ {{p 1}^{3}}}+{4 \ {{p 0}^{2}}\ p 1}\right)}\ p 3}\right)}\ q 0 \ q 1}+{{\left(-{2 \ p 0 \ {{p 3}^{3}}}+{{\left({2 \ p 0 \ {{p 2}^{2}}}-{2 \ p 0 \ {{p 1}^{2}}}-{{p 0}^{3}}\right)}\ p 3}\right)}\ {{q 0}^{2}}}\right)}\ q 2}+{2 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 1}^{3}}}+{{\left(-{3 \ {{p 1}^{2}}}-{2 \ {{p 0}^{2}}}\right)}\ p 2 \ p 3 \ q 0 \ {{q 1}^{2}}}+{4 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 0}^{2}}\ q 1}-{{{p 0}^{2}}\ p 2 \ p 3 \ {{q 0}^{3}}}\right)}\ q 3}+{{\left(-{p 0 \ p 1 \ {{p 2}^{2}}\ q 1}+{{\left({{{p 2}^{2}}\ {{p 3}^{2}}}+{{{p 1}^{2}}\ {{p 2}^{2}}}\right)}\ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left({p 0 \ {{p 2}^{3}}}-{2 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ {{q 1}^{2}}}+{{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}-{p 1 \ {{p 2}^{3}}}+{{\left({2 \ {{p 1}^{3}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2}\right)}\ q 0 \ q 1}+{{\left(-{2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{2 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left({2 \ p 0 \ p 1 \ {{p 2}^{2}}}-{p 0 \ {{p 1}^{3}}}\right)}\ {{q 1}^{3}}}+{{\left({{{p 1}^{2}}\ {{p 3}^{2}}}+{{\left(-{2 \ {{p 1}^{2}}}-{2 \ {{p 0}^{2}}}\right)}\ {{p 2}^{2}}}+{{p 1}^{4}}+{2 \ {{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left(-{2 \ p 0 \ p 1 \ {{p 3}^{2}}}+{2 \ p 0 \ p 1 \ {{p 2}^{2}}}-{2 \ p 0 \ {{p 1}^{3}}}-{{{p 0}^{3}}\ p 1}\right)}\ {{q 0}^{2}}\ q 1}+{{\left({{{p 0}^{2}}\ {{p 3}^{2}}}+{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 0}^{3}}}\right)}\ q 2}+{p 0 \ {{p 1}^{2}}\ p 2 \ {{q 1}^{4}}}+{{\left(-{{p 1}^{3}}-{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2 \ q 0 \ {{q 1}^{3}}}+{{\left({2 \ p 0 \ {{p 1}^{2}}}+{{p 0}^{3}}\right)}\ p 2 \ {{q 0}^{2}}\ {{q 1}^{2}}}-{{{p 0}^{2}}\ p 1 \ p 2 \ {{q 0}^{3}}\ q 1}}&{-{p 1 \ p 2 \ {{p 3}^{2}}\ {{q 3}^{4}}}+{{\left({{\left({p 1 \ {{p 3}^{3}}}-{2 \ p 1 \ {{p 2}^{2}}\ p 3}\right)}\ q 2}+{{\left({p 2 \ {{p 3}^{3}}}-{2 \ {{p 1}^{2}}\ p 2 \ p 3}\right)}\ q 1}+{2 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}-{p 1 \ {{p 2}^{3}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{{p 3}^{4}}+{{\left({2 \ {{p 2}^{2}}}+{2 \ {{p 1}^{2}}}+{{p 0}^{2}}\right)}\ {{p 3}^{2}}}-{2 \ {{p 1}^{2}}\ {{p 2}^{2}}}\right)}\ q 1}+{{\left(-{3 \ p 0 \ p 1 \ {{p 3}^{2}}}+{2 \ p 0 \ p 1 \ {{p 2}^{2}}}\right)}\ q 0}\right)}\ q 2}+{{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}-{{{p 1}^{3}}\ p 2}\right)}\ {{q 1}^{2}}}+{{\left(-{3 \ p 0 \ p 2 \ {{p 3}^{2}}}+{2 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ q 0 \ q 1}+{{\left({p 1 \ p 2 \ {{p 3}^{2}}}-{{{p 0}^{2}}\ p 1 \ p 2}\right)}\ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left({p 1 \ {{p 2}^{2}}\ p 3 \ {{q 2}^{3}}}+{{\left({{\left(-{2 \ p 2 \ {{p 3}^{3}}}+{{\left({{p 2}^{3}}+{{\left({2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ p 2}\right)}\ p 3}\right)}\ q 1}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{2 \ p 1 \ {{p 3}^{3}}}+{{\left({2 \ p 1 \ {{p 2}^{2}}}+{{p 1}^{3}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3}\right)}\ {{q 1}^{2}}}+{{\left({2 \ p 0 \ {{p 3}^{3}}}+{{\left(-{4 \ p 0 \ {{p 2}^{2}}}-{4 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 3}\right)}\ q 0 \ q 1}+{{\left({2 \ p 1 \ {{p 2}^{2}}}+{3 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ {{q 0}^{2}}}\right)}\ q 2}+{{{p 1}^{2}}\ p 2 \ p 3 \ {{q 1}^{3}}}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0 \ {{q 1}^{2}}}+{{\left({2 \ {{p 1}^{2}}}+{3 \ {{p 0}^{2}}}\right)}\ p 2 \ p 3 \ {{q 0}^{2}}\ q 1}-{2 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 0}^{3}}}\right)}\ q 3}+{{\left({{\left(-{{{p 2}^{2}}\ {{p 3}^{2}}}+{{{p 0}^{2}}\ {{p 2}^{2}}}\right)}\ q 1}-{p 0 \ p 1 \ {{p 2}^{2}}\ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left(-{2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{2 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ {{q 1}^{2}}}+{{\left({2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{p 0 \ {{p 2}^{3}}}+{{\left(-{2 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 2}\right)}\ q 0 \ q 1}+{{\left({p 1 \ {{p 2}^{3}}}+{2 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{{{p 1}^{2}}\ {{p 3}^{2}}}+{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 1}^{3}}}+{{\left({2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{2 \ p 0 \ p 1 \ {{p 2}^{2}}}-{p 0 \ {{p 1}^{3}}}-{2 \ {{p 0}^{3}}\ p 1}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left(-{{{p 0}^{2}}\ {{p 3}^{2}}}+{{\left({2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ {{p 2}^{2}}}+{2 \ {{p 0}^{2}}\ {{p 1}^{2}}}+{{p 0}^{4}}\right)}\ {{q 0}^{2}}\ q 1}+{{\left(-{2 \ p 0 \ p 1 \ {{p 2}^{2}}}-{{{p 0}^{3}}\ p 1}\right)}\ {{q 0}^{3}}}\right)}\ q 2}-{p 0 \ {{p 1}^{2}}\ p 2 \ q 0 \ {{q 1}^{3}}}+{{\left({{p 1}^{3}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2 \ {{q 0}^{2}}\ {{q 1}^{2}}}+{{\left(-{2 \ p 0 \ {{p 1}^{2}}}-{{p 0}^{3}}\right)}\ p 2 \ {{q 0}^{3}}\ q 1}+{{{p 0}^{2}}\ p 1 \ p 2 \ {{q 0}^{4}}}}&{-{{{p 2}^{2}}\ {{p 3}^{2}}\ {{q 3}^{4}}}+{{\left({{\left({2 \ p 2 \ {{p 3}^{3}}}-{2 \ {{p 2}^{3}}\ p 3}\right)}\ q 2}-{2 \ p 1 \ {{p 2}^{2}}\ p 3 \ q 1}+{2 \ p 0 \ {{p 2}^{2}}\ p 3 \ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left(-{{p 3}^{4}}+{{\left({4 \ {{p 2}^{2}}}-{{p 1}^{2}}+{{p 0}^{2}}\right)}\ {{p 3}^{2}}}-{{p 2}^{4}}\right)}\ {{q 2}^{2}}}+{{\left({{\left({6 \ p 1 \ p 2 \ {{p 3}^{2}}}-{2 \ p 1 \ {{p 2}^{3}}}\right)}\ q 1}+{{\left(-{6 \ p 0 \ p 2 \ {{p 3}^{2}}}+{2 \ p 0 \ {{p 2}^{3}}}\right)}\ q 0}\right)}\ q 2}+{{\left(-{{{p 2}^{2}}\ {{p 3}^{2}}}-{{{p 1}^{2}}\ {{p 2}^{2}}}\right)}\ {{q 1}^{2}}}+{2 \ p 0 \ p 1 \ {{p 2}^{2}}\ q 0 \ q 1}+{{\left({{{p 2}^{2}}\ {{p 3}^{2}}}-{{{p 0}^{2}}\ {{p 2}^{2}}}\right)}\ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left({{\left(-{2 \ p 2 \ {{p 3}^{3}}}+{{\left({2 \ {{p 2}^{3}}}+{{\left(-{2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ p 2}\right)}\ p 3}\right)}\ {{q 2}^{3}}}+{{\left({{\left(-{2 \ p 1 \ {{p 3}^{3}}}+{{\left({8 \ p 1 \ {{p 2}^{2}}}-{2 \ {{p 1}^{3}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3}\right)}\ q 1}+{{\left({2 \ p 0 \ {{p 3}^{3}}}+{{\left(-{8 \ p 0 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 3}\right)}\ q 0}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{2 \ {{p 2}^{3}}}+{6 \ {{p 1}^{2}}\ p 2}\right)}\ p 3 \ {{q 1}^{2}}}-{{12}\ p 0 \ p 1 \ p 2 \ p 3 \ q 0 \ q 1}+{{\left({2 \ {{p 2}^{3}}}+{6 \ {{p 0}^{2}}\ p 2}\right)}\ p 3 \ {{q 0}^{2}}}\right)}\ q 2}-{2 \ p 1 \ {{p 2}^{2}}\ p 3 \ {{q 1}^{3}}}+{2 \ p 0 \ {{p 2}^{2}}\ p 3 \ q 0 \ {{q 1}^{2}}}+{2 \ p 1 \ {{p 2}^{2}}\ p 3 \ {{q 0}^{2}}\ q 1}-{2 \ p 0 \ {{p 2}^{2}}\ p 3 \ {{q 0}^{3}}}\right)}\ q 3}+{{\left(-{{{p 2}^{2}}\ {{p 3}^{2}}}+{{\left(-{{p 1}^{2}}+{{p 0}^{2}}\right)}\ {{p 2}^{2}}}\right)}\ {{q 2}^{4}}}+{{\left({{\left(-{2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{2 \ p 1 \ {{p 2}^{3}}}+{{\left(-{2 \ {{p 1}^{3}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2}\right)}\ q 1}+{{\left({2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{2 \ p 0 \ {{p 2}^{3}}}+{{\left({2 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 2}\right)}\ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left(-{{{p 1}^{2}}\ {{p 3}^{2}}}-{{p 2}^{4}}+{4 \ {{p 1}^{2}}\ {{p 2}^{2}}}-{{p 1}^{4}}+{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 1}^{2}}}+{{\left({2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{8 \ p 0 \ p 1 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{3}}}-{2 \ {{p 0}^{3}}\ p 1}\right)}\ q 0 \ q 1}+{{\left(-{{{p 0}^{2}}\ {{p 3}^{2}}}+{{p 2}^{4}}+{4 \ {{p 0}^{2}}\ {{p 2}^{2}}}-{{{p 0}^{2}}\ {{p 1}^{2}}}+{{p 0}^{4}}\right)}\ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{2 \ p 1 \ {{p 2}^{3}}}+{2 \ {{p 1}^{3}}\ p 2}\right)}\ {{q 1}^{3}}}+{{\left({2 \ p 0 \ {{p 2}^{3}}}-{6 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left({2 \ p 1 \ {{p 2}^{3}}}+{6 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ {{q 0}^{2}}\ q 1}+{{\left(-{2 \ p 0 \ {{p 2}^{3}}}-{2 \ {{p 0}^{3}}\ p 2}\right)}\ {{q 0}^{3}}}\right)}\ q 2}-{{{p 1}^{2}}\ {{p 2}^{2}}\ {{q 1}^{4}}}+{2 \ p 0 \ p 1 \ {{p 2}^{2}}\ q 0 \ {{q 1}^{3}}}+{{\left({{p 1}^{2}}-{{p 0}^{2}}\right)}\ {{p 2}^{2}}\ {{q 0}^{2}}\ {{q 1}^{2}}}-{2 \ p 0 \ p 1 \ {{p 2}^{2}}\ {{q 0}^{3}}\ q 1}+{{{p 0}^{2}}\ {{p 2}^{2}}\ {{q 0}^{4}}}}&{{{\left({{\left(-{{p 1}^{2}}+{{p 0}^{2}}\right)}\ {{p 3}^{2}}\ q 2}+{p 1 \ p 2 \ {{p 3}^{2}}\ q 1}-{p 0 \ p 2 \ {{p 3}^{2}}\ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left(-{2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ p 2 \ p 3 \ {{q 2}^{2}}}+{{\left({{\left({p 1 \ {{p 3}^{3}}}+{{\left({2 \ p 1 \ {{p 2}^{2}}}-{2 \ {{p 1}^{3}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3}\right)}\ q 1}+{{\left(-{p 0 \ {{p 3}^{3}}}+{{\left(-{2 \ p 0 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 3}\right)}\ q 0}\right)}\ q 2}+{{\left(-{p 2 \ {{p 3}^{3}}}+{2 \ {{p 1}^{2}}\ p 2 \ p 3}\right)}\ {{q 1}^{2}}}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0 \ q 1}+{{\left({p 2 \ {{p 3}^{3}}}+{2 \ {{p 0}^{2}}\ p 2 \ p 3}\right)}\ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left({{\left(-{{p 1}^{2}}+{{p 0}^{2}}\right)}\ {{p 2}^{2}}\ {{q 2}^{3}}}+{{\left({{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{p 1 \ {{p 2}^{3}}}+{{\left(-{2 \ {{p 1}^{3}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2}\right)}\ q 1}+{{\left(-{2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{p 0 \ {{p 2}^{3}}}+{{\left({2 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 2}\right)}\ q 0}\right)}\ {{q 2}^{2}}}+{{\left({{\left({{\left(-{2 \ {{p 2}^{2}}}+{2 \ {{p 1}^{2}}}\right)}\ {{p 3}^{2}}}+{2 \ {{p 1}^{2}}\ {{p 2}^{2}}}-{{p 1}^{4}}+{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 1}^{2}}}+{{\left(-{4 \ p 0 \ p 1 \ {{p 3}^{2}}}-{4 \ p 0 \ p 1 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{3}}}-{2 \ {{p 0}^{3}}\ p 1}\right)}\ q 0 \ q 1}+{{\left({{\left({2 \ {{p 2}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ {{p 3}^{2}}}+{2 \ {{p 0}^{2}}\ {{p 2}^{2}}}-{{{p 0}^{2}}\ {{p 1}^{2}}}+{{p 0}^{4}}\right)}\ {{q 0}^{2}}}\right)}\ q 2}+{{\left(-{2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{{{p 1}^{3}}\ p 2}\right)}\ {{q 1}^{3}}}+{{\left({2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{3 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{3 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ {{q 0}^{2}}\ q 1}+{{\left(-{2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{{{p 0}^{3}}\ p 2}\right)}\ {{q 0}^{3}}}\right)}\ q 3}+{{\left({p 1 \ {{p 2}^{2}}\ p 3 \ q 1}-{p 0 \ {{p 2}^{2}}\ p 3 \ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left(-{{p 2}^{3}}+{2 \ {{p 1}^{2}}\ p 2}\right)}\ p 3 \ {{q 1}^{2}}}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0 \ q 1}+{{\left({{p 2}^{3}}+{2 \ {{p 0}^{2}}\ p 2}\right)}\ p 3 \ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{2 \ p 1 \ {{p 2}^{2}}}+{{p 1}^{3}}\right)}\ p 3 \ {{q 1}^{3}}}+{{\left({2 \ p 0 \ {{p 2}^{2}}}-{3 \ p 0 \ {{p 1}^{2}}}\right)}\ p 3 \ q 0 \ {{q 1}^{2}}}+{{\left({2 \ p 1 \ {{p 2}^{2}}}+{3 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ {{q 0}^{2}}\ q 1}+{{\left(-{2 \ p 0 \ {{p 2}^{2}}}-{{p 0}^{3}}\right)}\ p 3 \ {{q 0}^{3}}}\right)}\ q 2}-{{{p 1}^{2}}\ p 2 \ p 3 \ {{q 1}^{4}}}+{2 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0 \ {{q 1}^{3}}}+{{\left({{p 1}^{2}}-{{p 0}^{2}}\right)}\ p 2 \ p 3 \ {{q 0}^{2}}\ {{q 1}^{2}}}-{2 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 0}^{3}}\ q 1}+{{{p 0}^{2}}\ p 2 \ p 3 \ {{q 0}^{4}}}}
\
{{{\left(-{p 0 \ p 2 \ {{p 3}^{2}}\ q 2}-{p 0 \ p 1 \ {{p 3}^{2}}\ q 1}+{{\left({{p 2}^{2}}+{{p 1}^{2}}\right)}\ {{p 3}^{2}}\ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left({p 0 \ {{p 3}^{3}}}-{2 \ p 0 \ {{p 2}^{2}}\ p 3}\right)}\ {{q 2}^{2}}}+{{\left(-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 1}+{{\left(-{p 2 \ {{p 3}^{3}}}+{{\left({2 \ {{p 2}^{3}}}+{{\left({2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ p 2}\right)}\ p 3}\right)}\ q 0}\right)}\ q 2}+{{\left({p 0 \ {{p 3}^{3}}}-{2 \ p 0 \ {{p 1}^{2}}\ p 3}\right)}\ {{q 1}^{2}}}+{{\left(-{p 1 \ {{p 3}^{3}}}+{{\left({2 \ p 1 \ {{p 2}^{2}}}+{2 \ {{p 1}^{3}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3}\right)}\ q 0 \ q 1}+{{\left(-{2 \ p 0 \ {{p 2}^{2}}}-{2 \ p 0 \ {{p 1}^{2}}}\right)}\ p 3 \ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left({{\left({2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{p 0 \ {{p 2}^{3}}}\right)}\ {{q 2}^{3}}}+{{\left({{\left({2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{3 \ p 0 \ p 1 \ {{p 2}^{2}}}\right)}\ q 1}+{{\left({{\left(-{2 \ {{p 2}^{2}}}-{2 \ {{p 0}^{2}}}\right)}\ {{p 3}^{2}}}+{{p 2}^{4}}+{{\left({{p 1}^{2}}+{2 \ {{p 0}^{2}}}\right)}\ {{p 2}^{2}}}\right)}\ q 0}\right)}\ {{q 2}^{2}}}+{{\left({{\left({2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{3 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ {{q 1}^{2}}}+{{\left(-{4 \ p 1 \ p 2 \ {{p 3}^{2}}}+{2 \ p 1 \ {{p 2}^{3}}}+{{\left({2 \ {{p 1}^{3}}}+{4 \ {{p 0}^{2}}\ p 1}\right)}\ p 2}\right)}\ q 0 \ q 1}+{{\left({2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{2 \ p 0 \ {{p 2}^{3}}}+{{\left(-{2 \ p 0 \ {{p 1}^{2}}}-{{p 0}^{3}}\right)}\ p 2}\right)}\ {{q 0}^{2}}}\right)}\ q 2}+{{\left({2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{p 0 \ {{p 1}^{3}}}\right)}\ {{q 1}^{3}}}+{{\left({{\left(-{2 \ {{p 1}^{2}}}-{2 \ {{p 0}^{2}}}\right)}\ {{p 3}^{2}}}+{{{p 1}^{2}}\ {{p 2}^{2}}}+{{p 1}^{4}}+{2 \ {{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left({2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{2 \ p 0 \ p 1 \ {{p 2}^{2}}}-{2 \ p 0 \ {{p 1}^{3}}}-{{{p 0}^{3}}\ p 1}\right)}\ {{q 0}^{2}}\ q 1}+{{\left({{{p 0}^{2}}\ {{p 2}^{2}}}+{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 0}^{3}}}\right)}\ q 3}+{p 0 \ {{p 2}^{2}}\ p 3 \ {{q 2}^{4}}}+{{\left({2 \ p 0 \ p 1 \ p 2 \ p 3 \ q 1}+{{\left(-{{p 2}^{3}}-{2 \ {{p 0}^{2}}\ p 2}\right)}\ p 3 \ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left({p 0 \ {{p 2}^{2}}}+{p 0 \ {{p 1}^{2}}}\right)}\ p 3 \ {{q 1}^{2}}}+{{\left(-{3 \ p 1 \ {{p 2}^{2}}}-{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ q 0 \ q 1}+{{\left({2 \ p 0 \ {{p 2}^{2}}}+{{p 0}^{3}}\right)}\ p 3 \ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({2 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 1}^{3}}}+{{\left(-{3 \ {{p 1}^{2}}}-{2 \ {{p 0}^{2}}}\right)}\ p 2 \ p 3 \ q 0 \ {{q 1}^{2}}}+{4 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 0}^{2}}\ q 1}-{{{p 0}^{2}}\ p 2 \ p 3 \ {{q 0}^{3}}}\right)}\ q 2}+{p 0 \ {{p 1}^{2}}\ p 3 \ {{q 1}^{4}}}+{{\left(-{{p 1}^{3}}-{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ q 0 \ {{q 1}^{3}}}+{{\left({2 \ p 0 \ {{p 1}^{2}}}+{{p 0}^{3}}\right)}\ p 3 \ {{q 0}^{2}}\ {{q 1}^{2}}}-{{{p 0}^{2}}\ p 1 \ p 3 \ {{q 0}^{3}}\ q 1}}&{{{\left({p 1 \ p 2 \ {{p 3}^{2}}\ q 2}+{{\left(-{{p 2}^{2}}+{{p 0}^{2}}\right)}\ {{p 3}^{2}}\ q 1}-{p 0 \ p 1 \ {{p 3}^{2}}\ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left(-{p 1 \ {{p 3}^{3}}}+{2 \ p 1 \ {{p 2}^{2}}\ p 3}\right)}\ {{q 2}^{2}}}+{{\left({{\left({p 2 \ {{p 3}^{3}}}+{{\left(-{2 \ {{p 2}^{3}}}+{{\left({2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ p 2}\right)}\ p 3}\right)}\ q 1}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0}\right)}\ q 2}+{{\left(-{2 \ p 1 \ {{p 2}^{2}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ {{q 1}^{2}}}+{{\left(-{p 0 \ {{p 3}^{3}}}+{{\left({2 \ p 0 \ {{p 2}^{2}}}-{2 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 3}\right)}\ q 0 \ q 1}+{{\left({p 1 \ {{p 3}^{3}}}+{2 \ {{p 0}^{2}}\ p 1 \ p 3}\right)}\ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left({{\left(-{2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{p 1 \ {{p 2}^{3}}}\right)}\ {{q 2}^{3}}}+{{\left({{\left({{\left({2 \ {{p 2}^{2}}}-{2 \ {{p 1}^{2}}}\right)}\ {{p 3}^{2}}}-{{p 2}^{4}}+{{\left({2 \ {{p 1}^{2}}}+{{p 0}^{2}}\right)}\ {{p 2}^{2}}}\right)}\ q 1}+{{\left({2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{3 \ p 0 \ p 1 \ {{p 2}^{2}}}\right)}\ q 0}\right)}\ {{q 2}^{2}}}+{{\left({{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}-{2 \ p 1 \ {{p 2}^{3}}}+{{\left({{p 1}^{3}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2}\right)}\ {{q 1}^{2}}}+{{\left(-{4 \ p 0 \ p 2 \ {{p 3}^{2}}}+{2 \ p 0 \ {{p 2}^{3}}}+{{\left(-{4 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 2}\right)}\ q 0 \ q 1}+{{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{3 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ {{q 0}^{2}}}\right)}\ q 2}+{{\left(-{{{p 1}^{2}}\ {{p 2}^{2}}}+{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 1}^{3}}}+{{\left(-{2 \ p 0 \ p 1 \ {{p 3}^{2}}}+{2 \ p 0 \ p 1 \ {{p 2}^{2}}}-{p 0 \ {{p 1}^{3}}}-{2 \ {{p 0}^{3}}\ p 1}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left({{\left({2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ {{p 3}^{2}}}-{{{p 0}^{2}}\ {{p 2}^{2}}}+{2 \ {{p 0}^{2}}\ {{p 1}^{2}}}+{{p 0}^{4}}\right)}\ {{q 0}^{2}}\ q 1}+{{\left(-{2 \ p 0 \ p 1 \ {{p 3}^{2}}}-{{{p 0}^{3}}\ p 1}\right)}\ {{q 0}^{3}}}\right)}\ q 3}-{p 1 \ {{p 2}^{2}}\ p 3 \ {{q 2}^{4}}}+{{\left({{\left({{p 2}^{3}}-{2 \ {{p 1}^{2}}\ p 2}\right)}\ p 3 \ q 1}+{2 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left({2 \ p 1 \ {{p 2}^{2}}}-{{p 1}^{3}}\right)}\ p 3 \ {{q 1}^{2}}}+{{\left(-{3 \ p 0 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{2}}}\right)}\ p 3 \ q 0 \ q 1}+{{\left({p 1 \ {{p 2}^{2}}}-{{{p 0}^{2}}\ p 1}\right)}\ p 3 \ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({{{p 1}^{2}}\ p 2 \ p 3 \ {{q 1}^{3}}}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0 \ {{q 1}^{2}}}+{{\left({2 \ {{p 1}^{2}}}+{3 \ {{p 0}^{2}}}\right)}\ p 2 \ p 3 \ {{q 0}^{2}}\ q 1}-{2 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 0}^{3}}}\right)}\ q 2}-{p 0 \ {{p 1}^{2}}\ p 3 \ q 0 \ {{q 1}^{3}}}+{{\left({{p 1}^{3}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ {{q 0}^{2}}\ {{q 1}^{2}}}+{{\left(-{2 \ p 0 \ {{p 1}^{2}}}-{{p 0}^{3}}\right)}\ p 3 \ {{q 0}^{3}}\ q 1}+{{{p 0}^{2}}\ p 1 \ p 3 \ {{q 0}^{4}}}}&{{{\left({{\left(-{{p 1}^{2}}+{{p 0}^{2}}\right)}\ {{p 3}^{2}}\ q 2}+{p 1 \ p 2 \ {{p 3}^{2}}\ q 1}-{p 0 \ p 2 \ {{p 3}^{2}}\ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left(-{2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ p 2 \ p 3 \ {{q 2}^{2}}}+{{\left({{\left({p 1 \ {{p 3}^{3}}}+{{\left({2 \ p 1 \ {{p 2}^{2}}}-{2 \ {{p 1}^{3}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3}\right)}\ q 1}+{{\left(-{p 0 \ {{p 3}^{3}}}+{{\left(-{2 \ p 0 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 3}\right)}\ q 0}\right)}\ q 2}+{{\left(-{p 2 \ {{p 3}^{3}}}+{2 \ {{p 1}^{2}}\ p 2 \ p 3}\right)}\ {{q 1}^{2}}}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0 \ q 1}+{{\left({p 2 \ {{p 3}^{3}}}+{2 \ {{p 0}^{2}}\ p 2 \ p 3}\right)}\ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left({{\left(-{{p 1}^{2}}+{{p 0}^{2}}\right)}\ {{p 2}^{2}}\ {{q 2}^{3}}}+{{\left({{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{p 1 \ {{p 2}^{3}}}+{{\left(-{2 \ {{p 1}^{3}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2}\right)}\ q 1}+{{\left(-{2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{p 0 \ {{p 2}^{3}}}+{{\left({2 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 2}\right)}\ q 0}\right)}\ {{q 2}^{2}}}+{{\left({{\left({{\left(-{2 \ {{p 2}^{2}}}+{2 \ {{p 1}^{2}}}\right)}\ {{p 3}^{2}}}+{2 \ {{p 1}^{2}}\ {{p 2}^{2}}}-{{p 1}^{4}}+{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 1}^{2}}}+{{\left(-{4 \ p 0 \ p 1 \ {{p 3}^{2}}}-{4 \ p 0 \ p 1 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{3}}}-{2 \ {{p 0}^{3}}\ p 1}\right)}\ q 0 \ q 1}+{{\left({{\left({2 \ {{p 2}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ {{p 3}^{2}}}+{2 \ {{p 0}^{2}}\ {{p 2}^{2}}}-{{{p 0}^{2}}\ {{p 1}^{2}}}+{{p 0}^{4}}\right)}\ {{q 0}^{2}}}\right)}\ q 2}+{{\left(-{2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{{{p 1}^{3}}\ p 2}\right)}\ {{q 1}^{3}}}+{{\left({2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{3 \ p 0 \ {{p 1}^{2}}\ p 2}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left({2 \ p 1 \ p 2 \ {{p 3}^{2}}}+{3 \ {{p 0}^{2}}\ p 1 \ p 2}\right)}\ {{q 0}^{2}}\ q 1}+{{\left(-{2 \ p 0 \ p 2 \ {{p 3}^{2}}}-{{{p 0}^{3}}\ p 2}\right)}\ {{q 0}^{3}}}\right)}\ q 3}+{{\left({p 1 \ {{p 2}^{2}}\ p 3 \ q 1}-{p 0 \ {{p 2}^{2}}\ p 3 \ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left(-{{p 2}^{3}}+{2 \ {{p 1}^{2}}\ p 2}\right)}\ p 3 \ {{q 1}^{2}}}-{4 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0 \ q 1}+{{\left({{p 2}^{3}}+{2 \ {{p 0}^{2}}\ p 2}\right)}\ p 3 \ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{2 \ p 1 \ {{p 2}^{2}}}+{{p 1}^{3}}\right)}\ p 3 \ {{q 1}^{3}}}+{{\left({2 \ p 0 \ {{p 2}^{2}}}-{3 \ p 0 \ {{p 1}^{2}}}\right)}\ p 3 \ q 0 \ {{q 1}^{2}}}+{{\left({2 \ p 1 \ {{p 2}^{2}}}+{3 \ {{p 0}^{2}}\ p 1}\right)}\ p 3 \ {{q 0}^{2}}\ q 1}+{{\left(-{2 \ p 0 \ {{p 2}^{2}}}-{{p 0}^{3}}\right)}\ p 3 \ {{q 0}^{3}}}\right)}\ q 2}-{{{p 1}^{2}}\ p 2 \ p 3 \ {{q 1}^{4}}}+{2 \ p 0 \ p 1 \ p 2 \ p 3 \ q 0 \ {{q 1}^{3}}}+{{\left({{p 1}^{2}}-{{p 0}^{2}}\right)}\ p 2 \ p 3 \ {{q 0}^{2}}\ {{q 1}^{2}}}-{2 \ p 0 \ p 1 \ p 2 \ p 3 \ {{q 0}^{3}}\ q 1}+{{{p 0}^{2}}\ p 2 \ p 3 \ {{q 0}^{4}}}}&{{{\left(-{{p 2}^{2}}-{{p 1}^{2}}+{{p 0}^{2}}\right)}\ {{p 3}^{2}}\ {{q 3}^{4}}}+{{\left({{\left({2 \ p 2 \ {{p 3}^{3}}}+{{\left(-{2 \ {{p 2}^{3}}}+{{\left(-{2 \ {{p 1}^{2}}}+{2 \ {{p 0}^{2}}}\right)}\ p 2}\right)}\ p 3}\right)}\ q 2}+{{\left({2 \ p 1 \ {{p 3}^{3}}}+{{\left(-{2 \ p 1 \ {{p 2}^{2}}}-{2 \ {{p 1}^{3}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 3}\right)}\ q 1}+{{\left(-{2 \ p 0 \ {{p 3}^{3}}}+{{\left({2 \ p 0 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 3}\right)}\ q 0}\right)}\ {{q 3}^{3}}}+{{\left({{\left(-{{p 3}^{4}}+{4 \ {{p 2}^{2}}\ {{p 3}^{2}}}-{{p 2}^{4}}+{{\left(-{{p 1}^{2}}+{{p 0}^{2}}\right)}\ {{p 2}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left({{\left({8 \ p 1 \ p 2 \ {{p 3}^{2}}}-{2 \ p 1 \ {{p 2}^{3}}}+{{\left(-{2 \ {{p 1}^{3}}}+{2 \ {{p 0}^{2}}\ p 1}\right)}\ p 2}\right)}\ q 1}+{{\left(-{8 \ p 0 \ p 2 \ {{p 3}^{2}}}+{2 \ p 0 \ {{p 2}^{3}}}+{{\left({2 \ p 0 \ {{p 1}^{2}}}-{2 \ {{p 0}^{3}}}\right)}\ p 2}\right)}\ q 0}\right)}\ q 2}+{{\left(-{{p 3}^{4}}+{4 \ {{p 1}^{2}}\ {{p 3}^{2}}}-{{{p 1}^{2}}\ {{p 2}^{2}}}-{{p 1}^{4}}+{{{p 0}^{2}}\ {{p 1}^{2}}}\right)}\ {{q 1}^{2}}}+{{\left(-{8 \ p 0 \ p 1 \ {{p 3}^{2}}}+{2 \ p 0 \ p 1 \ {{p 2}^{2}}}+{2 \ p 0 \ {{p 1}^{3}}}-{2 \ {{p 0}^{3}}\ p 1}\right)}\ q 0 \ q 1}+{{\left({{p 3}^{4}}+{4 \ {{p 0}^{2}}\ {{p 3}^{2}}}-{{{p 0}^{2}}\ {{p 2}^{2}}}-{{{p 0}^{2}}\ {{p 1}^{2}}}+{{p 0}^{4}}\right)}\ {{q 0}^{2}}}\right)}\ {{q 3}^{2}}}+{{\left({{\left(-{2 \ p 2 \ {{p 3}^{3}}}+{2 \ {{p 2}^{3}}\ p 3}\right)}\ {{q 2}^{3}}}+{{\left({{\left(-{2 \ p 1 \ {{p 3}^{3}}}+{6 \ p 1 \ {{p 2}^{2}}\ p 3}\right)}\ q 1}+{{\left({2 \ p 0 \ {{p 3}^{3}}}-{6 \ p 0 \ {{p 2}^{2}}\ p 3}\right)}\ q 0}\right)}\ {{q 2}^{2}}}+{{\left({{\left(-{2 \ p 2 \ {{p 3}^{3}}}+{6 \ {{p 1}^{2}}\ p 2 \ p 3}\right)}\ {{q 1}^{2}}}-{{12}\ p 0 \ p 1 \ p 2 \ p 3 \ q 0 \ q 1}+{{\left({2 \ p 2 \ {{p 3}^{3}}}+{6 \ {{p 0}^{2}}\ p 2 \ p 3}\right)}\ {{q 0}^{2}}}\right)}\ q 2}+{{\left(-{2 \ p 1 \ {{p 3}^{3}}}+{2 \ {{p 1}^{3}}\ p 3}\right)}\ {{q 1}^{3}}}+{{\left({2 \ p 0 \ {{p 3}^{3}}}-{6 \ p 0 \ {{p 1}^{2}}\ p 3}\right)}\ q 0 \ {{q 1}^{2}}}+{{\left({2 \ p 1 \ {{p 3}^{3}}}+{6 \ {{p 0}^{2}}\ p 1 \ p 3}\right)}\ {{q 0}^{2}}\ q 1}+{{\left(-{2 \ p 0 \ {{p 3}^{3}}}-{2 \ {{p 0}^{3}}\ p 3}\right)}\ {{q 0}^{3}}}\right)}\ q 3}-{{{p 2}^{2}}\ {{p 3}^{2}}\ {{q 2}^{4}}}+{{\left(-{2 \ p 1 \ p 2 \ {{p 3}^{2}}\ q 1}+{2 \ p 0 \ p 2 \ {{p 3}^{2}}\ q 0}\right)}\ {{q 2}^{3}}}+{{\left({{\left(-{{p 2}^{2}}-{{p 1}^{2}}\right)}\ {{p 3}^{2}}\ {{q 1}^{2}}}+{2 \ p 0 \ p 1 \ {{p 3}^{2}}\ q 0 \ q 1}+{{\left({{p 2}^{2}}-{{p 0}^{2}}\right)}\ {{p 3}^{2}}\ {{q 0}^{2}}}\right)}\ {{q 2}^{2}}}+{{\left(-{2 \ p 1 \ p 2 \ {{p 3}^{2}}\ {{q 1}^{3}}}+{2 \ p 0 \ p 2 \ {{p 3}^{2}}\ q 0 \ {{q 1}^{2}}}+{2 \ p 1 \ p 2 \ {{p 3}^{2}}\ {{q 0}^{2}}\ q 1}-{2 \ p 0 \ p 2 \ {{p 3}^{2}}\ {{q 0}^{3}}}\right)}\ q 2}-{{{p 1}^{2}}\ {{p 3}^{2}}\ {{q 1}^{4}}}+{2 \ p 0 \ p 1 \ {{p 3}^{2}}\ q 0 \ {{q 1}^{3}}}+{{\left({{p 1}^{2}}-{{p 0}^{2}}\right)}\ {{p 3}^{2}}\ {{q 0}^{2}}\ {{q 1}^{2}}}-{2 \ p 0 \ p 1 \ {{p 3}^{2}}\ {{q 0}^{3}}\ q 1}+{{{p 0}^{2}}\ {{p 3}^{2}}\ {{q 0}^{4}}}}

(51)

Type: Matrix(Expression(Integer))

fricas

trace((PP*QQ-QQ*PP))

$\label{eq52}0$

(52)

Type: Expression(Integer)

Unit

fricas

-(PP*QQ+QQ*PP)+PP+QQ;

Type: Matrix(Expression(Integer))

fricas

2/trace(%)*%;

Type: Matrix(Expression(Integer))

fricas

trace %

$\label{eq53}2$

(53)

Type: Expression(Integer)

fricas

n:=map(Simplify,-(SS*TT+TT*SS)+SS+TT);

Type: Matrix(Expression(Integer))

fricas

Is?(n = (SS-TT)*(SS-TT) )

$\label{eq54} \mbox{\rm true}$

(54)

Type: Boolean

fricas

N:=map(Simplify,2/trace(n)*n);

Type: Matrix(Expression(Integer))

fricas

Simplify trace N

$\label{eq55}2$

(55)

Type: Expression(Integer)

fricas

Is?(N*N=N)

$\label{eq56} \mbox{\rm true}$

(56)

Type: Boolean

fricas

Is?(SS*N=SS)

$\label{eq57} \mbox{\rm true}$

(57)

Type: Boolean

fricas

Is?(TT*N=TT)

$\label{eq58} \mbox{\rm true}$

(58)

Type: Boolean

fricas

Is?(N*SS=SS)

$\label{eq59} \mbox{\rm true}$

(59)

Type: Boolean

fricas

Is?(N*TT=TT)

$\label{eq60} \mbox{\rm true}$

(60)

Type: Boolean

fricas

-(PP*RR+RR*PP)+PP+RR;

Type: Matrix(Expression(Integer))

fricas

2/trace(%)*%

$\label{eq61}\left[ \begin{array}{cccc} {\frac{{2 \ {{p 0}^{2}}}- 2}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+{{p 0}^{2}}- 1}}& 0 & 0 & 0 \ 0 &{\frac{2 \ {{p 1}^{2}}}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+{{p 0}^{2}}- 1}}&{\frac{2 \ p 1 \ p 2}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+{{p 0}^{2}}- 1}}&{\frac{2 \ p 1 \ p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+{{p 0}^{2}}- 1}} \ 0 &{\frac{2 \ p 1 \ p 2}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+{{p 0}^{2}}- 1}}&{\frac{2 \ {{p 2}^{2}}}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+{{p 0}^{2}}- 1}}&{\frac{2 \ p 2 \ p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+{{p 0}^{2}}- 1}} \ 0 &{\frac{2 \ p 1 \ p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+{{p 0}^{2}}- 1}}&{\frac{2 \ p 2 \ p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+{{p 0}^{2}}- 1}}&{\frac{2 \ {{p 3}^{2}}}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+{{p 0}^{2}}- 1}}$

(61)

Type: Matrix(Expression(Integer))

fricas

-(SS*RR+RR*SS)+SS+RR;

Type: Matrix(Expression(Integer))

fricas

2/trace(%)*%

$\label{eq62}\left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \ 0 &{\frac{{s 1}^{2}}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}}}&{\frac{s 1 \ s 2}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}}}&{\frac{s 1 \ s 3}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}}} \ 0 &{\frac{s 1 \ s 2}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}}}&{\frac{{s 2}^{2}}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}}}&{\frac{s 2 \ s 3}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}}} \ 0 &{\frac{s 1 \ s 3}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}}}&{\frac{s 2 \ s 3}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}}}&{\frac{{s 3}^{2}}{{{s 3}^{2}}+{{s 2}^{2}}+{{s 1}^{2}}}}$

(62)

Type: Matrix(Expression(Integer))

fricas

-(UU*RR+RR*UU)+UU+RR;

Type: Matrix(Expression(Integer))

fricas

map(Simplify,2/trace(%)*%)

$\label{eq63}\left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0$

(63)

Type: Matrix(Expression(Integer))

fricas

-(UU*VV+VV*UU)+UU+VV;

Type: Matrix(Expression(Integer))

fricas

map(Simplify,2/trace(%)*%)

$\label{eq64}\left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0$

(64)

Type: Matrix(Expression(Integer))

Momentum

fricas

m:=map(x+->factor(numer x)/factor(denom x),-(PP*QQ+QQ*PP)/dot(P,Q)+PP+QQ)

$\label{eq65}\left[ \begin{array}{cccc} {{\left(q 0 + p 0 \right)}^{2}}& -{{\left(q 0 + p 0 \right)}\ {\left(q 1 + p 1 \right)}}& -{{\left(q 0 + p 0 \right)}\ {\left(q 2 + p 2 \right)}}& -{{\left(q 0 + p 0 \right)}\ {\left(q 3 + p 3 \right)}} \ {{\left(q 0 + p 0 \right)}\ {\left(q 1 + p 1 \right)}}& -{{\left(q 1 + p 1 \right)}^{2}}& -{{\left(q 1 + p 1 \right)}\ {\left(q 2 + p 2 \right)}}& -{{\left(q 1 + p 1 \right)}\ {\left(q 3 + p 3 \right)}} \ {{\left(q 0 + p 0 \right)}\ {\left(q 2 + p 2 \right)}}& -{{\left(q 1 + p 1 \right)}\ {\left(q 2 + p 2 \right)}}& -{{\left(q 2 + p 2 \right)}^{2}}& -{{\left(q 2 + p 2 \right)}\ {\left(q 3 + p 3 \right)}} \ {{\left(q 0 + p 0 \right)}\ {\left(q 3 + p 3 \right)}}& -{{\left(q 1 + p 1 \right)}\ {\left(q 3 + p 3 \right)}}& -{{\left(q 2 + p 2 \right)}\ {\left(q 3 + p 3 \right)}}& -{{\left(q 3 + p 3 \right)}^{2}}$

(65)

Type: Matrix(Fraction(Factored(SparseMultivariatePolynomial?(Integer,Kernel(Expression(Integer))))))

fricas

Is?(m = tensor(-(P+Q),(P+Q)))

$\label{eq66} \mbox{\rm true}$

(66)

Type: Boolean

fricas

factor trace m

$\label{eq67}\begin{array}{@{}l} \displaystyle -{\left({ \begin{array}{@{}l} \displaystyle {{q 3}^{2}}+{2 \ p 3 \ q 3}+{{q 2}^{2}}+{2 \ p 2 \ q 2}+{{q 1}^{2}}+{2 \ p 1 \ q 1}- \ \ \displaystyle {{q 0}^{2}}-{2 \ p 0 \ q 0}+{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}$

(67)

Type: Factored(SparseMultivariatePolynomial?(Integer,Kernel(Expression(Integer))))

fricas

M:=1/trace(m)*m::Matrix Scalar;

Type: Matrix(Expression(Integer))

fricas

trace M

$\label{eq68}1$

(68)

Type: Expression(Integer)

fricas

Is?(M*M=M)

$\label{eq69} \mbox{\rm true}$

(69)

Type: Boolean

fricas

(PP*RR+RR*PP)/dot(P,R)-PP-RR;

Type: Matrix(Expression(Integer))

fricas

1/trace(%)*%

$\label{eq70}\left[ \begin{array}{cccc} {\frac{-{{p 0}^{2}}-{2 \ p 0}- 1}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}}&{\frac{{\left(p 0 + 1 \right)}\ p 1}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}}&{\frac{{\left(p 0 + 1 \right)}\ p 2}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}}&{\frac{{\left(p 0 + 1 \right)}\ p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}} \ {\frac{{\left(- p 0 - 1 \right)}\ p 1}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}}&{\frac{{p 1}^{2}}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}}&{\frac{p 1 \ p 2}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}}&{\frac{p 1 \ p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}} \ {\frac{{\left(- p 0 - 1 \right)}\ p 2}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}}&{\frac{p 1 \ p 2}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}}&{\frac{{p 2}^{2}}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}}&{\frac{p 2 \ p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}} \ {\frac{{\left(- p 0 - 1 \right)}\ p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}}&{\frac{p 1 \ p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}}&{\frac{p 2 \ p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}}&{\frac{{p 3}^{2}}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}-{{p 0}^{2}}-{2 \ p 0}- 1}}$

(70)

Type: Matrix(Expression(Integer))

fricas

trace %

$\label{eq71}1$

(71)

Type: Expression(Integer)

fricas

--(SS*RR+RR*SS)/dot(S,R)-SS-RR;
--map(Simplify,1/trace(%)*%)
--(UU*VV+VV*UU)/dot(U,V)-UU-VV;
--1/trace(%)*%
(UU*RR+RR*UU)/dot(U,R)-UU-RR;

Type: Matrix(Expression(Integer))

fricas

map(Simplify,1/trace(%)*%)

$\label{eq72}\left[ \begin{array}{cccc} {\frac{{\cosh \left({3 \ u}\right)}+{4 \ {\cosh \left({2 \ u}\right)}}+{7 \ {\cosh \left({u}\right)}}+ 4}{{4 \ {\cosh \left({2 \ u}\right)}}+{8 \ {\cosh \left({u}\right)}}+ 4}}&{\frac{-{\sinh \left({3 \ u}\right)}-{2 \ {\sinh \left({2 \ u}\right)}}-{\sinh \left({u}\right)}}{{4 \ {\cosh \left({2 \ u}\right)}}+{8 \ {\cosh \left({u}\right)}}+ 4}}& 0 & 0 \ {\frac{{\sinh \left({3 \ u}\right)}+{2 \ {\sinh \left({2 \ u}\right)}}+{\sinh \left({u}\right)}}{{4 \ {\cosh \left({2 \ u}\right)}}+{8 \ {\cosh \left({u}\right)}}+ 4}}&{\frac{-{\cosh \left({3 \ u}\right)}+{\cosh \left({u}\right)}}{{4 \ {\cosh \left({2 \ u}\right)}}+{8 \ {\cosh \left({u}\right)}}+ 4}}& 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0$

(72)

Type: Matrix(Expression(Integer))

Unit for 3 Observers

fricas

P:=1/sqrt(1-p1^2-p2^2-p3^2)*vect [1,-p1,-p2,-p3]

$\label{eq73}\left[ \begin{array}{c} {\frac{1}{\sqrt{-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1}}} \ -{\frac{p 1}{\sqrt{-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1}}} \ -{\frac{p 2}{\sqrt{-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1}}} \ -{\frac{p 3}{\sqrt{-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1}}}$

(73)

Type: Matrix(Expression(Integer))

fricas

PP:=tensor(-P,P)

$\label{eq74}\left[ \begin{array}{cccc} -{\frac{1}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}}& -{\frac{p 1}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}}& -{\frac{p 2}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}}& -{\frac{p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}} \ {\frac{p 1}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}}&{\frac{{p 1}^{2}}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}}&{\frac{p 1 \ p 2}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}}&{\frac{p 1 \ p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}} \ {\frac{p 2}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}}&{\frac{p 1 \ p 2}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}}&{\frac{{p 2}^{2}}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}}&{\frac{p 2 \ p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}} \ {\frac{p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}}&{\frac{p 1 \ p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}}&{\frac{p 2 \ p 3}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}}&{\frac{{p 3}^{2}}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}}$

(74)

Type: Matrix(Expression(Integer))

fricas

Q:=1/sqrt(1-q1^2-q2^2-q3^2)*vect [1,-q1,-q2,-q3]

$\label{eq75}\left[ \begin{array}{c} {\frac{1}{\sqrt{-{{q 3}^{2}}-{{q 2}^{2}}-{{q 1}^{2}}+ 1}}} \ -{\frac{q 1}{\sqrt{-{{q 3}^{2}}-{{q 2}^{2}}-{{q 1}^{2}}+ 1}}} \ -{\frac{q 2}{\sqrt{-{{q 3}^{2}}-{{q 2}^{2}}-{{q 1}^{2}}+ 1}}} \ -{\frac{q 3}{\sqrt{-{{q 3}^{2}}-{{q 2}^{2}}-{{q 1}^{2}}+ 1}}}$

(75)

Type: Matrix(Expression(Integer))

fricas

QQ:=tensor(-Q,Q)

$\label{eq76}\left[ \begin{array}{cccc} -{\frac{1}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}}& -{\frac{q 1}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}}& -{\frac{q 2}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}}& -{\frac{q 3}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}} \ {\frac{q 1}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}}&{\frac{{q 1}^{2}}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}}&{\frac{q 1 \ q 2}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}}&{\frac{q 1 \ q 3}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}} \ {\frac{q 2}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}}&{\frac{q 1 \ q 2}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}}&{\frac{{q 2}^{2}}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}}&{\frac{q 2 \ q 3}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}} \ {\frac{q 3}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}}&{\frac{q 1 \ q 3}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}}&{\frac{q 2 \ q 3}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}}&{\frac{{q 3}^{2}}{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}- 1}}$

(76)

Type: Matrix(Expression(Integer))

fricas

R:=1/sqrt(1-r1^2-r2^2-r3^2)*vect [1,-r1,-r2,-r3]

$\label{eq77}\left[ \begin{array}{c} {\frac{1}{\sqrt{-{{r 3}^{2}}-{{r 2}^{2}}-{{r 1}^{2}}+ 1}}} \ -{\frac{r 1}{\sqrt{-{{r 3}^{2}}-{{r 2}^{2}}-{{r 1}^{2}}+ 1}}} \ -{\frac{r 2}{\sqrt{-{{r 3}^{2}}-{{r 2}^{2}}-{{r 1}^{2}}+ 1}}} \ -{\frac{r 3}{\sqrt{-{{r 3}^{2}}-{{r 2}^{2}}-{{r 1}^{2}}+ 1}}}$

(77)

Type: Matrix(Expression(Integer))

fricas

RR:=tensor(-R,R)

$\label{eq78}\left[ \begin{array}{cccc} -{\frac{1}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}}& -{\frac{r 1}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}}& -{\frac{r 2}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}}& -{\frac{r 3}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}} \ {\frac{r 1}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}}&{\frac{{r 1}^{2}}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}}&{\frac{r 1 \ r 2}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}}&{\frac{r 1 \ r 3}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}} \ {\frac{r 2}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}}&{\frac{r 1 \ r 2}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}}&{\frac{{r 2}^{2}}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}}&{\frac{r 2 \ r 3}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}} \ {\frac{r 3}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}}&{\frac{r 1 \ r 3}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}}&{\frac{r 2 \ r 3}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}}&{\frac{{r 3}^{2}}{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}- 1}}$

(78)

Type: Matrix(Expression(Integer))

fricas

gamma(p,q) == - dot(p,q)

Type: Void

fricas

-- Silberstein
f0 := - determinant(matrix [[1,gamma(P,Q),gamma(P,R)], _
                       [gamma(P,Q),1,gamma(Q,R)], _
                       [gamma(P,R),gamma(Q,R),1]] )

fricas

Compiling function gamma with type (Matrix(Expression(Integer)), 
      Matrix(Expression(Integer))) -> Expression(Integer)

$\label{eq79}\frac{{{\left({{\left(-{{p 1}^{2}}+ 1 \right)}\ {{q 2}^{2}}}+{{\left({2 \ p 1 \ p 2 \ q 1}-{2 \ p 2}\right)}\ q 2}+{{\left(-{{p 2}^{2}}+ 1 \right)}\ {{q 1}^{2}}}-{2 \ p 1 \ q 1}+{{p 2}^{2}}+{{p 1}^{2}}\right)}\ {{r 3}^{2}}}+{{\left({{\left({{\left({{\left({2 \ {{p 1}^{2}}}- 2 \right)}\ q 2}-{2 \ p 1 \ p 2 \ q 1}+{2 \ p 2}\right)}\ q 3}+{{\left(-{2 \ p 1 \ p 3 \ q 1}+{2 \ p 3}\right)}\ q 2}+{2 \ p 2 \ p 3 \ {{q 1}^{2}}}-{2 \ p 2 \ p 3}\right)}\ r 2}+{{\left({{\left(-{2 \ p 1 \ p 2 \ q 2}+{{\left({2 \ {{p 2}^{2}}}- 2 \right)}\ q 1}+{2 \ p 1}\right)}\ q 3}+{2 \ p 1 \ p 3 \ {{q 2}^{2}}}-{2 \ p 2 \ p 3 \ q 1 \ q 2}+{2 \ p 3 \ q 1}-{2 \ p 1 \ p 3}\right)}\ r 1}+{{\left({2 \ p 2 \ q 2}+{2 \ p 1 \ q 1}-{2 \ {{p 2}^{2}}}-{2 \ {{p 1}^{2}}}\right)}\ q 3}-{2 \ p 3 \ {{q 2}^{2}}}+{2 \ p 2 \ p 3 \ q 2}-{2 \ p 3 \ {{q 1}^{2}}}+{2 \ p 1 \ p 3 \ q 1}\right)}\ r 3}+{{\left({{\left(-{{p 1}^{2}}+ 1 \right)}\ {{q 3}^{2}}}+{{\left({2 \ p 1 \ p 3 \ q 1}-{2 \ p 3}\right)}\ q 3}+{{\left(-{{p 3}^{2}}+ 1 \right)}\ {{q 1}^{2}}}-{2 \ p 1 \ q 1}+{{p 3}^{2}}+{{p 1}^{2}}\right)}\ {{r 2}^{2}}}+{{\left({{\left({2 \ p 1 \ p 2 \ {{q 3}^{2}}}+{{\left(-{2 \ p 1 \ p 3 \ q 2}-{2 \ p 2 \ p 3 \ q 1}\right)}\ q 3}+{{\left({{\left({2 \ {{p 3}^{2}}}- 2 \right)}\ q 1}+{2 \ p 1}\right)}\ q 2}+{2 \ p 2 \ q 1}-{2 \ p 1 \ p 2}\right)}\ r 1}-{2 \ p 2 \ {{q 3}^{2}}}+{{\left({2 \ p 3 \ q 2}+{2 \ p 2 \ p 3}\right)}\ q 3}+{{\left({2 \ p 1 \ q 1}-{2 \ {{p 3}^{2}}}-{2 \ {{p 1}^{2}}}\right)}\ q 2}-{2 \ p 2 \ {{q 1}^{2}}}+{2 \ p 1 \ p 2 \ q 1}\right)}\ r 2}+{{\left({{\left(-{{p 2}^{2}}+ 1 \right)}\ {{q 3}^{2}}}+{{\left({2 \ p 2 \ p 3 \ q 2}-{2 \ p 3}\right)}\ q 3}+{{\left(-{{p 3}^{2}}+ 1 \right)}\ {{q 2}^{2}}}-{2 \ p 2 \ q 2}+{{p 3}^{2}}+{{p 2}^{2}}\right)}\ {{r 1}^{2}}}+{{\left(-{2 \ p 1 \ {{q 3}^{2}}}+{{\left({2 \ p 3 \ q 1}+{2 \ p 1 \ p 3}\right)}\ q 3}-{2 \ p 1 \ {{q 2}^{2}}}+{{\left({2 \ p 2 \ q 1}+{2 \ p 1 \ p 2}\right)}\ q 2}+{{\left(-{2 \ {{p 3}^{2}}}-{2 \ {{p 2}^{2}}}\right)}\ q 1}\right)}\ r 1}+{{\left({{p 2}^{2}}+{{p 1}^{2}}\right)}\ {{q 3}^{2}}}+{{\left(-{2 \ p 2 \ p 3 \ q 2}-{2 \ p 1 \ p 3 \ q 1}\right)}\ q 3}+{{\left({{p 3}^{2}}+{{p 1}^{2}}\right)}\ {{q 2}^{2}}}-{2 \ p 1 \ p 2 \ q 1 \ q 2}+{{\left({{p 3}^{2}}+{{p 2}^{2}}\right)}\ {{q 1}^{2}}}}{{{\left({{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 3}^{2}}}+{{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 2}^{2}}}+{{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 1}^{2}}}-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1 \right)}\ {{r 3}^{2}}}+{{\left({{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 3}^{2}}}+{{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 2}^{2}}}+{{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 1}^{2}}}-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1 \right)}\ {{r 2}^{2}}}+{{\left({{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 3}^{2}}}+{{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 2}^{2}}}+{{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 1}^{2}}}-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1 \right)}\ {{r 1}^{2}}}+{{\left(-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1 \right)}\ {{q 3}^{2}}}+{{\left(-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1 \right)}\ {{q 2}^{2}}}+{{\left(-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1 \right)}\ {{q 1}^{2}}}+{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}$

(79)

Type: Expression(Integer)

fricas

f:=gamma(P,Q)^2 + gamma(P,R)^2 + gamma(Q,R)^2 - 2*gamma(P,Q)*gamma(P,R)*gamma(Q,R) - 1

$\label{eq80}\frac{{{\left({{\left(-{{p 1}^{2}}+ 1 \right)}\ {{q 2}^{2}}}+{{\left({2 \ p 1 \ p 2 \ q 1}-{2 \ p 2}\right)}\ q 2}+{{\left(-{{p 2}^{2}}+ 1 \right)}\ {{q 1}^{2}}}-{2 \ p 1 \ q 1}+{{p 2}^{2}}+{{p 1}^{2}}\right)}\ {{r 3}^{2}}}+{{\left({{\left({{\left({{\left({2 \ {{p 1}^{2}}}- 2 \right)}\ q 2}-{2 \ p 1 \ p 2 \ q 1}+{2 \ p 2}\right)}\ q 3}+{{\left(-{2 \ p 1 \ p 3 \ q 1}+{2 \ p 3}\right)}\ q 2}+{2 \ p 2 \ p 3 \ {{q 1}^{2}}}-{2 \ p 2 \ p 3}\right)}\ r 2}+{{\left({{\left(-{2 \ p 1 \ p 2 \ q 2}+{{\left({2 \ {{p 2}^{2}}}- 2 \right)}\ q 1}+{2 \ p 1}\right)}\ q 3}+{2 \ p 1 \ p 3 \ {{q 2}^{2}}}-{2 \ p 2 \ p 3 \ q 1 \ q 2}+{2 \ p 3 \ q 1}-{2 \ p 1 \ p 3}\right)}\ r 1}+{{\left({2 \ p 2 \ q 2}+{2 \ p 1 \ q 1}-{2 \ {{p 2}^{2}}}-{2 \ {{p 1}^{2}}}\right)}\ q 3}-{2 \ p 3 \ {{q 2}^{2}}}+{2 \ p 2 \ p 3 \ q 2}-{2 \ p 3 \ {{q 1}^{2}}}+{2 \ p 1 \ p 3 \ q 1}\right)}\ r 3}+{{\left({{\left(-{{p 1}^{2}}+ 1 \right)}\ {{q 3}^{2}}}+{{\left({2 \ p 1 \ p 3 \ q 1}-{2 \ p 3}\right)}\ q 3}+{{\left(-{{p 3}^{2}}+ 1 \right)}\ {{q 1}^{2}}}-{2 \ p 1 \ q 1}+{{p 3}^{2}}+{{p 1}^{2}}\right)}\ {{r 2}^{2}}}+{{\left({{\left({2 \ p 1 \ p 2 \ {{q 3}^{2}}}+{{\left(-{2 \ p 1 \ p 3 \ q 2}-{2 \ p 2 \ p 3 \ q 1}\right)}\ q 3}+{{\left({{\left({2 \ {{p 3}^{2}}}- 2 \right)}\ q 1}+{2 \ p 1}\right)}\ q 2}+{2 \ p 2 \ q 1}-{2 \ p 1 \ p 2}\right)}\ r 1}-{2 \ p 2 \ {{q 3}^{2}}}+{{\left({2 \ p 3 \ q 2}+{2 \ p 2 \ p 3}\right)}\ q 3}+{{\left({2 \ p 1 \ q 1}-{2 \ {{p 3}^{2}}}-{2 \ {{p 1}^{2}}}\right)}\ q 2}-{2 \ p 2 \ {{q 1}^{2}}}+{2 \ p 1 \ p 2 \ q 1}\right)}\ r 2}+{{\left({{\left(-{{p 2}^{2}}+ 1 \right)}\ {{q 3}^{2}}}+{{\left({2 \ p 2 \ p 3 \ q 2}-{2 \ p 3}\right)}\ q 3}+{{\left(-{{p 3}^{2}}+ 1 \right)}\ {{q 2}^{2}}}-{2 \ p 2 \ q 2}+{{p 3}^{2}}+{{p 2}^{2}}\right)}\ {{r 1}^{2}}}+{{\left(-{2 \ p 1 \ {{q 3}^{2}}}+{{\left({2 \ p 3 \ q 1}+{2 \ p 1 \ p 3}\right)}\ q 3}-{2 \ p 1 \ {{q 2}^{2}}}+{{\left({2 \ p 2 \ q 1}+{2 \ p 1 \ p 2}\right)}\ q 2}+{{\left(-{2 \ {{p 3}^{2}}}-{2 \ {{p 2}^{2}}}\right)}\ q 1}\right)}\ r 1}+{{\left({{p 2}^{2}}+{{p 1}^{2}}\right)}\ {{q 3}^{2}}}+{{\left(-{2 \ p 2 \ p 3 \ q 2}-{2 \ p 1 \ p 3 \ q 1}\right)}\ q 3}+{{\left({{p 3}^{2}}+{{p 1}^{2}}\right)}\ {{q 2}^{2}}}-{2 \ p 1 \ p 2 \ q 1 \ q 2}+{{\left({{p 3}^{2}}+{{p 2}^{2}}\right)}\ {{q 1}^{2}}}}{{{\left({{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 3}^{2}}}+{{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 2}^{2}}}+{{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 1}^{2}}}-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1 \right)}\ {{r 3}^{2}}}+{{\left({{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 3}^{2}}}+{{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 2}^{2}}}+{{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 1}^{2}}}-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1 \right)}\ {{r 2}^{2}}}+{{\left({{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 3}^{2}}}+{{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 2}^{2}}}+{{\left({{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1 \right)}\ {{q 1}^{2}}}-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1 \right)}\ {{r 1}^{2}}}+{{\left(-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1 \right)}\ {{q 3}^{2}}}+{{\left(-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1 \right)}\ {{q 2}^{2}}}+{{\left(-{{p 3}^{2}}-{{p 2}^{2}}-{{p 1}^{2}}+ 1 \right)}\ {{q 1}^{2}}}+{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}- 1}$

(80)

Type: Expression(Integer)

fricas

test(f0 = f)

$\label{eq81} \mbox{\rm true}$

(81)

Type: Boolean

fricas

--
nf:=map(Simplify, (-gamma(P,Q)*gamma(P,R)+gamma(Q,R))/gamma(Q,R)*RR*QQ + _
                 (-gamma(Q,R)*gamma(Q,P)+gamma(R,P))/gamma(R,P)*RR*PP + _
                 (-gamma(P,Q)*gamma(P,R)+gamma(Q,R))/gamma(Q,R)*QQ*RR + _
                 (-gamma(R,Q)*gamma(R,P)+gamma(Q,P))/gamma(Q,P)*QQ*PP + _
                 (-gamma(Q,R)*gamma(Q,P)+gamma(R,P))/gamma(R,P)*PP*RR + _
                 (-gamma(R,Q)*gamma(R,P)+gamma(Q,P))/gamma(Q,P)*PP*QQ + _
                 (gamma(Q,R)^2-1)*PP + _
                 (gamma(P,Q)^2-1)*RR + _
                 (gamma(P,R)^2-1)*QQ );

Type: Matrix(Expression(Integer))

fricas

N := 1/f*nf;

Type: Matrix(Expression(Integer))

fricas

--N:=map(Simplify,3/trace(n)*n);
Simplify trace N

$\label{eq82}3$

(82)

Type: Expression(Integer)

fricas

Is?(N*N=N)

$\label{eq83} \mbox{\rm true}$

(83)

Type: Boolean

fricas

map(possible,N*N-N)

$\label{eq84}\left[ \begin{array}{cccc} 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0$

(84)

Type: Matrix(Expression(Integer))

fricas

Is?(PP*N=PP)

$\label{eq85} \mbox{\rm true}$

(85)

Type: Boolean

fricas

Is?(QQ*N=QQ)

$\label{eq86} \mbox{\rm true}$

(86)

Type: Boolean

fricas

Is?(RR*N=RR)

$\label{eq87} \mbox{\rm true}$

(87)

Type: Boolean

fricas

Is?(N*PP=PP)

$\label{eq88} \mbox{\rm true}$

(88)

Type: Boolean

fricas

Is?(N*QQ=QQ)

$\label{eq89} \mbox{\rm true}$

(89)

Type: Boolean

fricas

Is?(N*RR=RR)

$\label{eq90} \mbox{\rm true}$

(90)

Type: Boolean

Orthogonal Observers

fricas

PP' := N - (1/trace(PP))*PP

$\label{eq91}$

(91)

Type: Matrix(Expression(Integer))

fricas

Is?(PP'*PP' = PP')

$\label{eq92} \mbox{\rm true}$

(92)

Type: Boolean

fricas

trace PP'

$\label{eq93}2$

(93)

Type: Expression(Integer)

fricas

Is?(PP'*PP = 0*PP)

$\label{eq94} \mbox{\rm true}$

(94)

Type: Boolean

fricas

-- derivation
Is?(PP'*(QQ*RR) = (PP'*QQ)*RR + QQ*(PP'*RR))

$\label{eq95} \mbox{\rm false}$

(95)

Type: Boolean