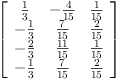Some or all of this page may not have rendered properly, because of the following error: dvips: cd '/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/'; /usr/bin/dvips -z -o 'SandBoxComplementsdalgebrelineaire.ps' 'SandBoxComplementsdalgebrelineaire.dvi' This is dvips(k) 2022.1 (TeX Live 2022) Copyright 2022 Radical Eye Software (www.radicaleye.com) /usr/bin/dvips: DVI file can't be opened: SandBoxComplementsdalgebrelineaire.dvi: No such file or directory fricas (1) -> --- --- linalg.input --- Francois Maltey - janvier 2008 --- --- --- A partir de rowEchelon --- sameSizeVectors? Lb == null Lb => true n := #(first Lb) every? (t +-> #t=n, Type: Void
fricas basis mat == mat2 := rowEchelon mat basis := [] indrow : Integer := 1 n : Integer := ncols mat m : Integer := nrows mat for k in 1..n repeat if indrow <= m and mat2.(indrow, Type: Void
fricas basisLV Lv == null Lv => [] not (sameSizeVectors? Lv) => error "vectors have not the same size" basis transpose matrix Lv Type: Void
fricas basisMat mat == basis mat Type: Void
fricas sumBasisLLV LLv == basisLV concat LLv Type: Void
fricas sumBasis2 (Lv1, Type: Void
fricas kernelMat mat == lv := nullSpace mat #lv = 1 and lv.1 = 0*lv.1 => [] lv Type: Void
fricas subVector (v, Type: Void
fricas linearVector (t, Type: Void
fricas intBasis2 (Lv1, Type: Void
fricas intBasisLLV LLv == #LLv = 0 => error "no space to intersect" #LLv = 1 => LLv.1 --reduce (intBasis2, Type: Void
fricas --- --- inversegeneralisee.input --- Francois Maltey - janvier 2008 --- --- inverse generalisee --- --- a partir du livre Algebre lineaire par Joseph Grifone p.375 --- applique pas à pas la méthode du livre à l'exemple
Type: Matrix(Integer)
fricas --- kerA est une base de ker f ou f est definie par la matrice A fricas Compiling function kernelMat with type Matrix(Integer) -> List(
Vector(Integer))
Type: List(Vector(Integer))
fricas --- Le noyau de la matrice dont les lignes sont des vecteurs generateurs --- d'un sev est le sev orthogonal. C'est un sous-espace supplementaire. --- baseF est une base d'un sous-espace supplémentaire de ker f
Type: List(Vector(Integer))
fricas --- les vecteurs colonnes de A engendre l'image Im f. --- baseImA est une base de l'image de f calculee a partir de la matrice A
Type: List(Vector(Integer))
fricas --- baseG et baseG2 sont deux bases d'un sous-espace supplementaire de Im f --- l'une calculee a partir de la matrice A,
Type: List(Vector(Integer))
fricas baseG2:= kernelMat matrix baseImA
Type: List(Vector(Integer))
fricas --- La restriction g de f est un isomorphisme du supplementaire F de ker f --- dans Im f. La matrice de g dans les bases de F et de Im f est obtenue --- en decomposant dans Im f les images des vecteurs de la base de F. --- La commande particularSolution effectue cette decomposition.
Type: Matrix(Integer)
fricas map (X +-> A*X,
Type: List(Vector(Integer))
fricas map (X +-> particularSolution (MP,
Type: List(Union(Vector(Fraction(Integer)),
fricas B := transpose matrix map (X +-> particularSolution (MP,
Type: Matrix(Fraction(Integer))
fricas --- La matrice C est celle de l'isomorphisme reciproque dans ces bases.
Type: Matrix(Fraction(Integer))
fricas --- la projection orthogonale de E' sur Im f peut être obtenue --- à partir d'une base orthonormee de Im f. --- baseImA est une base de Im f,
Type: List(Matrix(Expression(Integer)))
fricas bonImA := map (M +-> column (M,
Type: List(Vector(Expression(Integer)))
fricas projortho X == reduce (+, Type: Void
fricas --- exemple de projection orthogonale sur Im f. fricas Compiling function projortho with type Vector(PositiveInteger) ->
Vector(Expression(Integer))
Type: Vector(Expression(Integer))
fricas --- construction de la composition g^-1 o p de E' dans E --- en calculant les images des vecteurs de la base canonique de E' --- puis passage des coordonnees de g^-1 o p de la base de F --- à la base canonique de E.
Type: Matrix(Integer)
fricas RES1 := [projortho column (Id3, fricas Compiling function projortho with type Vector(Integer) -> Vector(
Expression(Integer))
Type: List(Vector(Expression(Integer)))
fricas RES2 := [X::Vector Fraction Integer for X in RES1]
Type: List(Vector(Fraction(Integer)))
fricas RES3 := [particularSolution (MP,
Type: List(Union(Vector(Fraction(Integer)),
fricas RES := [C * X for X in RES3::List Vector Fraction Integer]
Type: List(Vector(Fraction(Integer)))
fricas AA := transpose matrix baseF * transpose matrix RES
Type: Matrix(Fraction(Integer))
fricas --- vérifications de quelques propriétés : A AA A = A et AA A AA = AA --- transpose (A AA) = A AA : car les sev choisis sont des orthogonaux
Type: Matrix(Fraction(Integer))
fricas A * AA * A - A
Type: Matrix(Fraction(Integer))
fricas transpose (AA * A) - AA * A
Type: Matrix(Fraction(Integer))
fricas transpose (A * AA) - A * AA
Type: Matrix(Fraction(Integer))
|
|
|
|
last edited 17 years ago by Bill Page |


![\label{eq13}\begin{array}{@{}l}
\displaystyle
\left[{
\begin{array}{@{}l}
\displaystyle
\left[ -{\frac{2}{7 \ {\sqrt{\frac{3}{14}}}}}, \:{\frac{5}{{1
4}\ {\sqrt{\frac{3}{14}}}}}, \: \right.
\
\
\displaystyle
\left.{\frac{1}{{14}\ {\sqrt{\frac{3}{14}}}}}\right]
\label{eq13}\begin{array}{@{}l}
\displaystyle
\left[{
\begin{array}{@{}l}
\displaystyle
\left[ -{\frac{2}{7 \ {\sqrt{\frac{3}{14}}}}}, \:{\frac{5}{{1
4}\ {\sqrt{\frac{3}{14}}}}}, \: \right.
\
\
\displaystyle
\left.{\frac{1}{{14}\ {\sqrt{\frac{3}{14}}}}}\right]](images/4644723353892274016-16.0px.png)

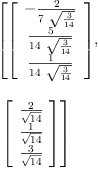
![\label{eq16}\begin{array}{@{}l}
\displaystyle
\left[{\left[{\frac{2}{3}}, \: -{\frac{1}{3}}, \:{\frac{1}{3}}\right]}, \:{\left[ -{\frac{1}{3}}, \:{\frac{2}{3}}, \:{\frac{1}{3}}\right]}, \: \right.
\
\
\displaystyle
\left.{\left[{\frac{1}{3}}, \:{\frac{1}{3}}, \:{\frac{2}{3}}\right]}\right]
\label{eq16}\begin{array}{@{}l}
\displaystyle
\left[{\left[{\frac{2}{3}}, \: -{\frac{1}{3}}, \:{\frac{1}{3}}\right]}, \:{\left[ -{\frac{1}{3}}, \:{\frac{2}{3}}, \:{\frac{1}{3}}\right]}, \: \right.
\
\
\displaystyle
\left.{\left[{\frac{1}{3}}, \:{\frac{1}{3}}, \:{\frac{2}{3}}\right]}\right]](images/3277902147330198291-16.0px.png)
![\label{eq17}\begin{array}{@{}l}
\displaystyle
\left[{\left[{\frac{2}{3}}, \: -{\frac{1}{3}}, \:{\frac{1}{3}}\right]}, \:{\left[ -{\frac{1}{3}}, \:{\frac{2}{3}}, \:{\frac{1}{3}}\right]}, \: \right.
\
\
\displaystyle
\left.{\left[{\frac{1}{3}}, \:{\frac{1}{3}}, \:{\frac{2}{3}}\right]}\right]
\label{eq17}\begin{array}{@{}l}
\displaystyle
\left[{\left[{\frac{2}{3}}, \: -{\frac{1}{3}}, \:{\frac{1}{3}}\right]}, \:{\left[ -{\frac{1}{3}}, \:{\frac{2}{3}}, \:{\frac{1}{3}}\right]}, \: \right.
\
\
\displaystyle
\left.{\left[{\frac{1}{3}}, \:{\frac{1}{3}}, \:{\frac{2}{3}}\right]}\right]](images/4569631786452881426-16.0px.png)
![\label{eq19}\begin{array}{@{}l}
\displaystyle
\left[{\left[ -{\frac{2}{3}}, \: -{\frac{1}{3}}\right]}, \:{\left[{\frac{1
1}{15}}, \:{\frac{7}{15}}\right]}, \: \right.
\
\
\displaystyle
\left.{\left[{\frac{1}{15}}, \:{\frac{2}{15}}\right]}\right]
\label{eq19}\begin{array}{@{}l}
\displaystyle
\left[{\left[ -{\frac{2}{3}}, \: -{\frac{1}{3}}\right]}, \:{\left[{\frac{1
1}{15}}, \:{\frac{7}{15}}\right]}, \: \right.
\
\
\displaystyle
\left.{\left[{\frac{1}{15}}, \:{\frac{2}{15}}\right]}\right]](images/5611008943178484563-16.0px.png)