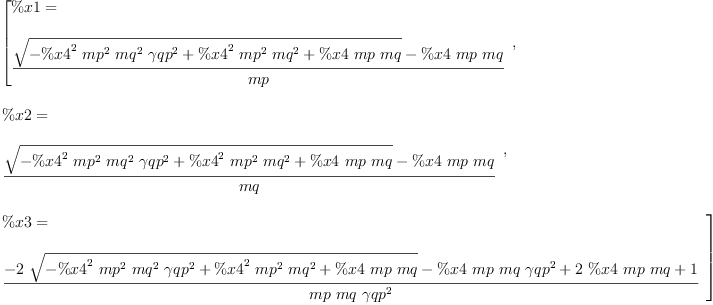MathAction SandBoxAlgebraOfObservers2

Topics

FrontPage
- SandBox
  - SandBoxObserverAsIdempotent
    - SandBoxObserverAsIdempotent2
      - SandBoxAlgebraOfObservers2 <-- You are here.

Obs(2) is a 4 dimensional Frobenius Algebra

Generators of Obs(2)

fricas

(1) -> )set output abbreviate on

fricas

)set message type off

V := OrderedVariableList [p,q]

$\label{eq1}\hbox{\axiomType{OVAR}\ } \left({\left[ p , \: q \right]}\right)$

(1)

fricas

vars:List V := enumerate()$V

$\label{eq2}\left[ p , \: q \right]$

(2)

--Representation

fricas

M := FreeMonoid V

$\label{eq3}\hbox{\axiomType{FMONOID}\ } \left({\hbox{\axiomType{OVAR}\ } \left({\left[ p , \: q \right]}\right)}\right)$

(3)

fricas

divisible := Record(lm: M,rm: M)

$\label{eq4}\hbox{\axiomType{Record}\ } \left({{lm :{\hbox{\axiomType{FMONOID}\ } \left({\hbox{\axiomType{OVAR}\ } \left({\left[ p , \: q \right]}\right)}\right)}}, \:{rm :{\hbox{\axiomType{FMONOID}\ } \left({\hbox{\axiomType{OVAR}\ } \left({\left[ p , \: q \right]}\right)}\right)}}}\right)$

(4)

fricas

gamma(i:Symbol,j:Symbol):Symbol == 
  concat([string 'γ,string i,string j])::Symbol

   Function declaration gamma : (SYMBOL, SYMBOL) -> SYMBOL has been 
      added to workspace.
  --subscript('γ,[concat(string i, string j)::Symbol])
mass(i:Symbol):Symbol ==
  concat("m",string i)::Symbol

   Function declaration mass : SYMBOL -> SYMBOL has been added to 
      workspace.
  --subscript('m,[i])
B := OrderedVariableList(concat [ ['x1,'x2,'x3,'x4], _
  [mass i for i in vars], _
  concat [[gamma(vars i ,vars j) for i in (j+1)..#vars] for j in 1..#vars] ])

fricas

Compiling function mass with type SYMBOL -> SYMBOL

fricas

Compiling function gamma with type (SYMBOL, SYMBOL) -> SYMBOL

$\label{eq5}\hbox{\axiomType{OVAR}\ } \left({\left[ x 1, \: x 2, \: x 3, \: x 4, \: mp , \: mq , \: �� qp \right]}\right)$

(5)

fricas

K := FRAC SMP(Integer,B)

$\label{eq6}\hbox{\axiomType{FRAC}\ } \left({\hbox{\axiomType{SMP}\ } \left({\hbox{\axiomType{INT}\ } , \:{\hbox{\axiomType{OVAR}\ } \left({\left[ x 1, \: x 2, \: x 3, \: x 4, \: mp , \: mq , \: �� qp \right]}\right)}}\right)}\right)$

(6)

fricas

MK := FreeModule(K,M)

$\label{eq7}FM \left({{\hbox{\axiomType{FRAC}\ } \left({\hbox{\axiomType{SMP}\ } \left({\hbox{\axiomType{INT}\ } , \:{\hbox{\axiomType{OVAR}\ } \left({\left[ x 1, \: x 2, \: x 3, \: x 4, \: mp , \: mq , \: �� qp \right]}\right)}}\right)}\right)}, \:{\hbox{\axiomType{FMONOID}\ } \left({\hbox{\axiomType{OVAR}\ } \left({\left[ p , \: q \right]}\right)}\right)}}\right)$

(7)

fricas

m(x:V):K == mass(x::Symbol)

   Function declaration m : OVAR([p,q]) -> FRAC(SMP(INT,OVAR([x1,x2,x3,
      x4,mp,mq,γqp]))) has been added to workspace.
m(vars 1)

fricas

Compiling function m with type OVAR([p,q]) -> FRAC(SMP(INT,OVAR([x1,
      x2,x3,x4,mp,mq,γqp])))

$\label{eq8}mp$

(8)

fricas

γ(x:V,y:V):K ==
  if x<y then
    return variable(gamma(x::Symbol,y::Symbol))$B
  if x>y then
    return variable(gamma(y::Symbol,x::Symbol))$B
  return 1

   Function declaration γ : (OVAR([p,q]), OVAR([p,q])) -> FRAC(SMP(INT,
      OVAR([x1,x2,x3,x4,mp,mq,γqp]))) has been added to workspace.
   Compiled code for gamma has been cleared.
γ(vars 2,vars 1)

fricas

Compiling function gamma with type (SYMBOL, SYMBOL) -> SYMBOL

fricas

Compiling function γ with type (OVAR([p,q]), OVAR([p,q])) -> FRAC(
      SMP(INT,OVAR([x1,x2,x3,x4,mp,mq,γqp])))

$\label{eq9}�� qp$

(9)

fricas

--Basis
basis:List M := concat(vars,concat [[i::M*j::M for j in vars | i~=j] for i in vars])

$\label{eq10}\left[ p , \: q , \:{p \ q}, \:{q \ p}\right]$

(10)

Idempotent: ii --> mᵢ γᵢᵢ i

fricas

idem(p:MK):MK ==
  -- p = c*q
  q := leadingSupport p
  c := leadingCoefficient p
  for i in vars::List M repeat
    f := divide(q, i*i)
    if f case divisible then -- q = f.lm * ii * f.rm
      return monomial(c * m i * γ(i,i), elt(f,lm) * i * elt(f,rm))
      --return monomial(c * γ(i,i), elt(f,lm) * i * elt(f,rm))
  return p

   Function declaration idem : FM(FRAC(SMP(INT,OVAR([x1,x2,x3,x4,mp,mq,
      γqp]))),FMONOID(OVAR([p,q]))) -> FM(FRAC(SMP(INT,OVAR([x1,x2,x3,
      x4,mp,mq,γqp]))),FMONOID(OVAR([p,q]))) has been added to 
      workspace.
idem(basis(1)*basis(1))

fricas

Compiling function idem with type FM(FRAC(SMP(INT,OVAR([x1,x2,x3,x4,
      mp,mq,γqp]))),FMONOID(OVAR([p,q]))) -> FM(FRAC(SMP(INT,OVAR([x1,
      x2,x3,x4,mp,mq,γqp]))),FMONOID(OVAR([p,q])))

$\label{eq11}mp \ p$

(11)

Reductions: ijk --> mᵢmⱼ γᵢⱼγⱼₖ/γᵢₖ ik

fricas

reduct(p:MK):MK ==
  q := leadingSupport p
  c := leadingCoefficient p
  for i in vars repeat
    for j in vars::List M | j ~= i repeat
      for k in vars::List M | k ~= j repeat
        f:=divide(q, i*j*k)
        if f case divisible then
          return monomial(c * m j * γ(i,j) * γ(j,k) / γ(i,k), _
          --return monomial(c * γ(i,j) * γ(j,k) / γ(i,k), _
                     elt(f,lm) * i * k * elt(f,rm))
  return p

   Function declaration reduct : FM(FRAC(SMP(INT,OVAR([x1,x2,x3,x4,mp,
      mq,γqp]))),FMONOID(OVAR([p,q]))) -> FM(FRAC(SMP(INT,OVAR([x1,x2,
      x3,x4,mp,mq,γqp]))),FMONOID(OVAR([p,q]))) has been added to 
      workspace.
reduct(basis(1)*basis(2)*basis(1))

fricas

Compiling function reduct with type FM(FRAC(SMP(INT,OVAR([x1,x2,x3,
      x4,mp,mq,γqp]))),FMONOID(OVAR([p,q]))) -> FM(FRAC(SMP(INT,OVAR([
      x1,x2,x3,x4,mp,mq,γqp]))),FMONOID(OVAR([p,q])))

$\label{eq12}{{�� qp}^{2}}\ mq \ {{p}^{2}}$

(12)

An endomorphism on the K-Module is defined by the fixed point of applied rules

fricas

Y(p:MK):MK ==
  repeat
    r := p; p := idem reduct r
    if r=p then return p

   Function declaration Y : FM(FRAC(SMP(INT,OVAR([x1,x2,x3,x4,mp,mq,γqp
      ]))),FMONOID(OVAR([p,q]))) -> FM(FRAC(SMP(INT,OVAR([x1,x2,x3,x4,
      mp,mq,γqp]))),FMONOID(OVAR([p,q]))) has been added to workspace.
Y(basis(1)*basis(2))

fricas

Compiling function Y with type FM(FRAC(SMP(INT,OVAR([x1,x2,x3,x4,mp,
      mq,γqp]))),FMONOID(OVAR([p,q]))) -> FM(FRAC(SMP(INT,OVAR([x1,x2,
      x3,x4,mp,mq,γqp]))),FMONOID(OVAR([p,q])))

$\label{eq13}p \ q$

(13)

Matrix

Algebra is the free algebra product modulo the fixed point

fricas

MT := [[Y(i*j) for j in basis] for i in basis]; matrix MT

$\label{eq14}\left[ \begin{array}{cccc} {mp \ p}&{p \ q}&{mp \ p \ q}&{{{�� qp}^{2}}\ mq \ mp \ p} \ {q \ p}&{mq \ q}&{{{�� qp}^{2}}\ mq \ mp \ q}&{mq \ q \ p} \ {{{�� qp}^{2}}\ mq \ mp \ p}&{mq \ p \ q}&{{{�� qp}^{2}}\ mq \ mp \ p \ q}&{{{�� qp}^{2}}\ {{mq}^{2}}\ mp \ p} \ {mp \ q \ p}&{{{�� qp}^{2}}\ mq \ mp \ q}&{{{�� qp}^{2}}\ mq \ {{mp}^{2}}\ q}&{{{�� qp}^{2}}\ mq \ mp \ q \ p}$

(14)

Structure Constants

fricas

mat3(y:M):List List K == map(z+->map(x+->coefficient(x,y),z),MT)

   Function declaration mat3 : FMONOID(OVAR([p,q])) -> LIST(LIST(FRAC(
      SMP(INT,OVAR([x1,x2,x3,x4,mp,mq,γqp]))))) has been added to 
      workspace.
ss:=map(mat3, basis); map(matrix,ss)

fricas

Compiling function mat3 with type FMONOID(OVAR([p,q])) -> LIST(LIST(
      FRAC(SMP(INT,OVAR([x1,x2,x3,x4,mp,mq,γqp])))))

$\label{eq15}\begin{array}{@{}l} \displaystyle \left[{\left[ \begin{array}{cccc} mp & 0 & 0 &{{{�� qp}^{2}}\ mq \ mp} \ 0 & 0 & 0 & 0 \ {{{�� qp}^{2}}\ mq \ mp}& 0 & 0 &{{{�� qp}^{2}}\ {{mq}^{2}}\ mp} \ 0 & 0 & 0 & 0$

(15)

Algebra

fricas

cats(m:M):Symbol==concat(map(x+->string(x.gen::Symbol),factors m))::Symbol

   Function declaration cats : FMONOID(OVAR([p,q])) -> SYMBOL has been 
      added to workspace.
A:=AlgebraGivenByStructuralConstants(K,#(basis)::PI,map(cats,basis),ss::Vector(Matrix K))

fricas

Compiling function cats with type FMONOID(OVAR([p,q])) -> SYMBOL

$\label{eq16}\hbox{\axiomType{ALGSC}\ } \left({{\hbox{\axiomType{FRAC}\ } \left({\hbox{\axiomType{SMP}\ } \left({\hbox{\axiomType{INT}\ } , \:{\hbox{\axiomType{OVAR}\ } \left({\left[ x 1, \: x 2, \: x 3, \: x 4, \: mp , \: mq , \: �� qp \right]}\right)}}\right)}\right)}, \: 4, \:{\left[ p , \: q , \: pq , \: qp \right]}, \:{\left[{\left[ \begin{array}{cccc} mp & 0 & 0 &{{{�� qp}^{2}}\ mq \ mp} \ 0 & 0 & 0 & 0 \ {{{�� qp}^{2}}\ mq \ mp}& 0 & 0 &{{{�� qp}^{2}}\ {{mq}^{2}}\ mp} \ 0 & 0 & 0 & 0$

(16)

fricas

alternative?()$A

   algebra satisfies 2*associator(a,b,b) = 0 = 2*associator(a,a,b) = 0

$\label{eq17} \mbox{\rm true}$

(17)

fricas

antiAssociative?()$A

   algebra is not anti-associative

$\label{eq18} \mbox{\rm false}$

(18)

fricas

antiCommutative?()$A

   algebra is not anti-commutative

$\label{eq19} \mbox{\rm false}$

(19)

fricas

associative?()$A

   algebra is associative

$\label{eq20} \mbox{\rm true}$

(20)

fricas

commutative?()$A

   algebra is not commutative

$\label{eq21} \mbox{\rm false}$

(21)

fricas

flexible?()$A

   algebra is flexible

$\label{eq22} \mbox{\rm true}$

(22)

fricas

jacobiIdentity?()$A

   Jacobi identity does not hold

$\label{eq23} \mbox{\rm false}$

(23)

fricas

jordanAdmissible?()$A

   algebra is not Jordan admissible

$\label{eq24} \mbox{\rm false}$

(24)

fricas

jordanAlgebra?()$A

   algebra is not commutative
   this is not a Jordan algebra

$\label{eq25} \mbox{\rm false}$

(25)

fricas

leftAlternative?()$A

   algebra is left alternative

$\label{eq26} \mbox{\rm true}$

(26)

fricas

lieAdmissible?()$A

   algebra is Lie admissible

$\label{eq27} \mbox{\rm true}$

(27)

fricas

lieAlgebra?()$A

   algebra is not anti-commutative
   this is not a Lie algebra

$\label{eq28} \mbox{\rm false}$

(28)

fricas

--powerAssociative?()$A
rightAlternative?()$A

   algebra is right alternative

$\label{eq29} \mbox{\rm true}$

(29)

Check Multiplication

fricas

AB := entries basis()$A

$\label{eq30}\left[ p , \: q , \: pq , \: qp \right]$

(30)

fricas

A2MK(z:A):MK==reduce(+,map((x:K,y:M):MK+->(x::K)*y,coordinates(z),basis))

   Function declaration A2MK : ALGSC(FRAC(SMP(INT,OVAR([x1,x2,x3,x4,mp,
      mq,γqp]))),4,[p,q,pq,qp],[[[mp,0,0,γqp^2*mq*mp],[0,0,0,0],[γqp^2*
      mq*mp,0,0,γqp^2*mq^2*mp],[0,0,0,0]],[[0,0,0,0],[0,mq,γqp^2*mq*mp,
      0],[0,0,0,0],[0,γqp^2*mq*mp,γqp^2*mq*mp^2,0]],[[0,1,mp,0],[0,0,0,
      0],[0,mq,γqp^2*mq*mp,0],[0,0,0,0]],[[0,0,0,0],[1,0,0,mq],[0,0,0,0
      ],[mp,0,0,γqp^2*mq*mp]]]) -> FM(FRAC(SMP(INT,OVAR([x1,x2,x3,x4,mp
      ,mq,γqp]))),FMONOID(OVAR([p,q]))) has been added to workspace.
test(MT=map(x+->map(A2MK,x),[[i*j for j in AB] for i in AB]))

fricas

Compiling function A2MK with type ALGSC(FRAC(SMP(INT,OVAR([x1,x2,x3,
      x4,mp,mq,γqp]))),4,[p,q,pq,qp],[[[mp,0,0,γqp^2*mq*mp],[0,0,0,0],[
      γqp^2*mq*mp,0,0,γqp^2*mq^2*mp],[0,0,0,0]],[[0,0,0,0],[0,mq,γqp^2*
      mq*mp,0],[0,0,0,0],[0,γqp^2*mq*mp,γqp^2*mq*mp^2,0]],[[0,1,mp,0],[
      0,0,0,0],[0,mq,γqp^2*mq*mp,0],[0,0,0,0]],[[0,0,0,0],[1,0,0,mq],[0
      ,0,0,0],[mp,0,0,γqp^2*mq*mp]]]) -> FM(FRAC(SMP(INT,OVAR([x1,x2,x3
      ,x4,mp,mq,γqp]))),FMONOID(OVAR([p,q])))

$\label{eq31} \mbox{\rm true}$

(31)

Trace

fricas

[rightTrace(i)$A for i in AB]

$\label{eq32}\left[{2 \ mp}, \:{2 \ mq}, \:{2 \ {{�� qp}^{2}}\ mq \ mp}, \:{2 \ {{�� qp}^{2}}\ mq \ mp}\right]$

(32)

fricas

[leftTrace(i)$A for i in AB]

$\label{eq33}\left[{2 \ mp}, \:{2 \ mq}, \:{2 \ {{�� qp}^{2}}\ mq \ mp}, \:{2 \ {{�� qp}^{2}}\ mq \ mp}\right]$

(33)

fricas

trace(i)==rightTrace(i) / #vars

[trace(i) for i in AB]

fricas

Compiling function trace with type ALGSC(FRAC(SMP(INT,OVAR([x1,x2,x3
      ,x4,mp,mq,γqp]))),4,[p,q,pq,qp],[[[mp,0,0,γqp^2*mq*mp],[0,0,0,0],
      [γqp^2*mq*mp,0,0,γqp^2*mq^2*mp],[0,0,0,0]],[[0,0,0,0],[0,mq,γqp^2
      *mq*mp,0],[0,0,0,0],[0,γqp^2*mq*mp,γqp^2*mq*mp^2,0]],[[0,1,mp,0],
      [0,0,0,0],[0,mq,γqp^2*mq*mp,0],[0,0,0,0]],[[0,0,0,0],[1,0,0,mq],[
      0,0,0,0],[mp,0,0,γqp^2*mq*mp]]]) -> FRAC(SMP(INT,OVAR([x1,x2,x3,
      x4,mp,mq,γqp])))

$\label{eq34}\left[ mp , \: mq , \:{{{�� qp}^{2}}\ mq \ mp}, \:{{{�� qp}^{2}}\ mq \ mp}\right]$

(34)

fricas

p:=AB(1); q:=AB(2);

test(p*p=trace(p)*p)

$\label{eq35} \mbox{\rm true}$

(35)

fricas

test(q*q=trace(q)*q)

$\label{eq36} \mbox{\rm true}$

(36)

Center

fricas

C:=basisOfCenter()$AlgebraPackage(K,A); # C

$\label{eq37}1$

(37)

fricas

c:=C(1)

$\label{eq38}qp + pq -{mp \ q}-{mq \ p}$

(38)

fricas

[c*i-i*c for i in AB]

$\label{eq39}\left[ 0, \: 0, \: 0, \: 0 \right]$

(39)

fricas

c*c

$\label{eq40}\begin{array}{@{}l} \displaystyle {{\left({{�� qp}^{2}}- 1 \right)}\ mq \ mp \ qp}+{{\left({{�� qp}^{2}}- 1 \right)}\ mq \ mp \ pq}+ \ \ \displaystyle {{\left(-{{�� qp}^{2}}+ 1 \right)}\ mq \ {{mp}^{2}}\ q}+{{\left(-{{�� qp}^{2}}+ 1 \right)}\ {{mq}^{2}}\ mp \ p}$

(40)

fricas

test(c*c=c)

$\label{eq41} \mbox{\rm false}$

(41)

Unit

fricas

n := #vars/trace(c) * c

$\label{eq42}\begin{array}{@{}l} \displaystyle {{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq \ mp}}\ qp}+{{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq \ mp}}\ pq}- \ \ \displaystyle {{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq}}\ q}-{{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mp}}\ p}$

(42)

fricas

test(n = unit()$A)

$\label{eq43} \mbox{\rm true}$

(43)

fricas

trace(n)

$\label{eq44}2$

(44)

fricas

test(n*n=n)

$\label{eq45} \mbox{\rm true}$

(45)

fricas

f:=gcd map(x+->denom x,coordinates(n))

$\label{eq46}{{�� qp}^{2}}- 1$

(46)

fricas

--Silberstein symmetric matrix
ff:= matrix [[(i=j => 1$K; γ(i,j)) for j in vars] for i in vars]

$\label{eq47}\left[ \begin{array}{cc} 1 & �� qp \ �� qp & 1$

(47)

fricas

test(f = - determinant(ff))

$\label{eq48} \mbox{\rm true}$

(48)

fricas

(f*n)::OutputForm / f::OutputForm

$\label{eq49}\frac{{{\frac{1}{mq \ mp}}\ qp}+{{\frac{1}{mq \ mp}}\ pq}-{{\frac{1}{mq}}\ q}-{{\frac{1}{mp}}\ p}}{{{�� qp}^{2}}- 1}$

(49)

Orthogonal Observers

fricas

dual(p) == trace(p)*n - p

--dual(p) == n - (1/trace(p))*p
p' := dual p

fricas

Compiling function dual with type ALGSC(FRAC(SMP(INT,OVAR([x1,x2,x3,
      x4,mp,mq,γqp]))),4,[p,q,pq,qp],[[[mp,0,0,γqp^2*mq*mp],[0,0,0,0],[
      γqp^2*mq*mp,0,0,γqp^2*mq^2*mp],[0,0,0,0]],[[0,0,0,0],[0,mq,γqp^2*
      mq*mp,0],[0,0,0,0],[0,γqp^2*mq*mp,γqp^2*mq*mp^2,0]],[[0,1,mp,0],[
      0,0,0,0],[0,mq,γqp^2*mq*mp,0],[0,0,0,0]],[[0,0,0,0],[1,0,0,mq],[0
      ,0,0,0],[mp,0,0,γqp^2*mq*mp]]]) -> ALGSC(FRAC(SMP(INT,OVAR([x1,x2
      ,x3,x4,mp,mq,γqp]))),4,[p,q,pq,qp],[[[mp,0,0,γqp^2*mq*mp],[0,0,0,
      0],[γqp^2*mq*mp,0,0,γqp^2*mq^2*mp],[0,0,0,0]],[[0,0,0,0],[0,mq,
      γqp^2*mq*mp,0],[0,0,0,0],[0,γqp^2*mq*mp,γqp^2*mq*mp^2,0]],[[0,1,
      mp,0],[0,0,0,0],[0,mq,γqp^2*mq*mp,0],[0,0,0,0]],[[0,0,0,0],[1,0,0
      ,mq],[0,0,0,0],[mp,0,0,γqp^2*mq*mp]]])

$\label{eq50}\begin{array}{@{}l} \displaystyle {{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq}}\ qp}+{{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq}}\ pq}- \ \ \displaystyle {{\frac{mp}{{\left({{�� qp}^{2}}- 1 \right)}\ mq}}\ q}-{{\frac{{�� qp}^{2}}{{{�� qp}^{2}}- 1}}\ p}$

(50)

fricas

trace p'

$\label{eq51}mp$

(51)

fricas

p'' := dual p'

$\label{eq52}p$

(52)

fricas

trace p''

$\label{eq53}mp$

(53)

fricas

test(p' * p' = trace(p')*p')

$\label{eq54} \mbox{\rm true}$

(54)

fricas

p * p'

$\label{eq55}0$

(55)

fricas

p' * p

$\label{eq56}0$

(56)

fricas

q' := dual q

$\label{eq57}\begin{array}{@{}l} \displaystyle {{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mp}}\ qp}+{{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mp}}\ pq}- \ \ \displaystyle {{\frac{{�� qp}^{2}}{{{�� qp}^{2}}- 1}}\ q}-{{\frac{mq}{{\left({{�� qp}^{2}}- 1 \right)}\ mp}}\ p}$

(57)

fricas

trace(q')

$\label{eq58}mq$

(58)

fricas

test(q' * q' = trace(q')*q')

$\label{eq59} \mbox{\rm true}$

(59)

fricas

q * q'

$\label{eq60}0$

(60)

fricas

q' * q

$\label{eq61}0$

(61)

fricas

p' * q'

$\label{eq62}\begin{array}{@{}l} \displaystyle {{\frac{1}{{{�� qp}^{2}}- 1}}\ qp}+{{\frac{{�� qp}^{2}}{{{�� qp}^{2}}- 1}}\ pq}- \ \ \displaystyle {{\frac{{{�� qp}^{2}}\ mp}{{{�� qp}^{2}}- 1}}\ q}-{{\frac{{{�� qp}^{2}}\ mq}{{{�� qp}^{2}}- 1}}\ p}$

(62)

fricas

q' * p'

$\label{eq63}\begin{array}{@{}l} \displaystyle {{\frac{{�� qp}^{2}}{{{�� qp}^{2}}- 1}}\ qp}+{{\frac{1}{{{�� qp}^{2}}- 1}}\ pq}- \ \ \displaystyle {{\frac{{{�� qp}^{2}}\ mp}{{{�� qp}^{2}}- 1}}\ q}-{{\frac{{{�� qp}^{2}}\ mq}{{{�� qp}^{2}}- 1}}\ p}$

(63)

fricas

p' * q

$\label{eq64}- pq +{mp \ q}$

(64)

fricas

q * p'

$\label{eq65}- qp +{mp \ q}$

(65)

fricas

p * q'

$\label{eq66}- pq +{mq \ p}$

(66)

fricas

q' * p

$\label{eq67}- qp +{mq \ p}$

(67)

Orthogonal Observers are Derivations if there are only two observers

fricas

test(p'*(p*q) = (p'*p)*q + p*(p'*q))

$\label{eq68} \mbox{\rm true}$

(68)

fricas

test(q'*(p*q) = (q'*p)*q + p*(q'*q))

$\label{eq69} \mbox{\rm true}$

(69)

fricas

test((p*q)*p' = (p*p')*q + p*(q*p'))

$\label{eq70} \mbox{\rm true}$

(70)

fricas

test((p*q)*q' = (p*q')*q + p*(q*q'))

$\label{eq71} \mbox{\rm true}$

(71)

Momentum

fricas

P:=reduce(+,concat [[1/γ(basis i,basis j)*AB(i)*AB(j) for j in 1..size()$V] for i in 1..size()$V])

$\label{eq72}{{\frac{1}{�� qp}}\ qp}+{{\frac{1}{�� qp}}\ pq}+{mq \ q}+{mp \ p}$

(72)

fricas

trace(P)

$\label{eq73}{{mp}^{2}}+{2 \ �� qp \ mq \ mp}+{{mq}^{2}}$

(73)

fricas

u:=1/trace(P)*P

$\label{eq74}\begin{array}{@{}l} \displaystyle {{\frac{1}{{�� qp \ {{mp}^{2}}}+{2 \ {{�� qp}^{2}}\ mq \ mp}+{�� qp \ {{mq}^{2}}}}}\ qp}+ \ \ \displaystyle {{\frac{1}{{�� qp \ {{mp}^{2}}}+{2 \ {{�� qp}^{2}}\ mq \ mp}+{�� qp \ {{mq}^{2}}}}}\ pq}+ \ \ \displaystyle {{\frac{mq}{{{mp}^{2}}+{2 \ �� qp \ mq \ mp}+{{mq}^{2}}}}\ q}+ \ \ \displaystyle {{\frac{mp}{{{mp}^{2}}+{2 \ �� qp \ mq \ mp}+{{mq}^{2}}}}\ p}$

(74)

fricas

u*u-u

$\label{eq75}0$

(75)

fricas

trace(u)

$\label{eq76}1$

(76)

All idempotents

fricas

x:=x1*p+x2*q+x3*p*q+x4*q*p

   Compiled code for A2MK has been cleared.
   Compiled code for cats has been cleared.
   Compiled code for mat3 has been cleared.

$\label{eq77}{x 4 \ qp}+{x 3 \ pq}+{x 2 \ q}+{x 1 \ p}$

(77)

fricas

ideq:=conditionsForIdempotents()$GCNAALG(K,#(basis)::PI,map(cats,basis),ss::Vector(Matrix K))

fricas

Compiling function cats with type FMONOID(OVAR([p,q])) -> SYMBOL

$\label{eq78}\begin{array}{@{}l} \displaystyle \left[{ \begin{array}{@{}l} \displaystyle {{\left({{{�� qp}^{2}}\ {{mq}^{2}}\ mp \ \%x 3}+{{{�� qp}^{2}}\ mq \ mp \ \%x 1}\right)}\ \%x 4}+ \ \ \displaystyle {{{�� qp}^{2}}\ mq \ mp \ \%x 1 \ \%x 3}+{mp \ {{\%x 1}^{2}}}- \%x 1$

(78)

fricas

gbs:=groebnerFactorize ideq;

#gbs

$\label{eq79}9$

(79)

fricas

gbs.9

$\label{eq80}\begin{array}{@{}l} \displaystyle \left[{\%x 4 -{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq \ mp}}}, \:{\%x 3 -{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq \ mp}}}, \right. \ \ \displaystyle \left.\:{\%x 2 +{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq}}}, \:{\%x 1 +{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mp}}}\right]$

(80)

fricas

s9:=solve(gbs.9);

i9:=represents(reverse map(rhs,s9.1))$A

$\label{eq81}\begin{array}{@{}l} \displaystyle {{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq \ mp}}\ qp}+{{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq \ mp}}\ pq}- \ \ \displaystyle {{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq}}\ q}-{{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mp}}\ p}$

(81)

fricas

test(i9=n)

$\label{eq82} \mbox{\rm true}$

(82)

fricas

gbs.8

$\label{eq83}\begin{array}{@{}l} \displaystyle \left[{\%x 4 -{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq \ mp}}}, \: \right. \ \ \displaystyle \left.{\%x 3 -{\frac{1}{{\left({{�� qp}^{4}}-{{�� qp}^{2}}\right)}\ mq \ mp}}}, \:{\%x 2 +{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq}}}, \: \right. \ \ \displaystyle \left.{\%x 1 +{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mp}}}\right]$

(83)

fricas

s8:=solve(gbs.8);

i8:=represents(reverse map(rhs,s8.1))$A

$\label{eq84}\begin{array}{@{}l} \displaystyle {{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq \ mp}}\ qp}+{{\frac{1}{{\left({{�� qp}^{4}}-{{�� qp}^{2}}\right)}\ mq \ mp}}\ pq}- \ \ \displaystyle {{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq}}\ q}-{{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mp}}\ p}$

(84)

fricas

test(i8=n-1/trace(p*q)*p*q)

$\label{eq85} \mbox{\rm true}$

(85)

fricas

gbs.7

$\label{eq86}\begin{array}{@{}l} \displaystyle \left[{\%x 4 -{\frac{1}{{\left({{�� qp}^{4}}-{{�� qp}^{2}}\right)}\ mq \ mp}}}, \: \right. \ \ \displaystyle \left.{\%x 3 -{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq \ mp}}}, \:{\%x 2 +{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq}}}, \: \right. \ \ \displaystyle \left.{\%x 1 +{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mp}}}\right]$

(86)

fricas

s7:=solve(gbs.7);

i7:=represents(reverse map(rhs,s7.1))$A

$\label{eq87}\begin{array}{@{}l} \displaystyle {{\frac{1}{{\left({{�� qp}^{4}}-{{�� qp}^{2}}\right)}\ mq \ mp}}\ qp}+{{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq \ mp}}\ pq}- \ \ \displaystyle {{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mq}}\ q}-{{\frac{1}{{\left({{�� qp}^{2}}- 1 \right)}\ mp}}\ p}$

(87)

fricas

test(i7=n-1/trace(q*p)*q*p)

$\label{eq88} \mbox{\rm true}$

(88)

fricas

gbs.6

$\label{eq89}\left[{\%x 4 -{\frac{1}{{{�� qp}^{2}}\ mq \ mp}}}, \: \%x 3, \: \%x 2, \: \%x 1 \right]$

(89)

fricas

s6:=solve(gbs.6);

i6:=represents(reverse map(rhs,s6.1))$A

$\label{eq90}{\frac{1}{{{�� qp}^{2}}\ mq \ mp}}\ qp$

(90)

fricas

test(i6=1/trace(q*p)*q*p)

$\label{eq91} \mbox{\rm true}$

(91)

fricas

gbs.5

$\label{eq92}\left[ 1 \right]$

(92)

fricas

s5:=solve(gbs.5)

$\label{eq93}\left[ \right]$

(93)

fricas

gbs.4

$\label{eq94}\left[ \%x 4, \: \%x 3, \: \%x 2, \: \%x 1 \right]$

(94)

fricas

s4:=solve(gbs.4);

i4:=represents(reverse map(rhs,s4.1))$A

$\label{eq95}0$

(95)

fricas

gbs.3

$\label{eq96}\left[ \%x 4, \:{\%x 3 -{\frac{1}{{{�� qp}^{2}}\ mq \ mp}}}, \: \%x 2, \: \%x 1 \right]$

(96)

fricas

s3:=solve(gbs.3);

i3:=represents(reverse map(rhs,s3.1))$A

$\label{eq97}{\frac{1}{{{�� qp}^{2}}\ mq \ mp}}\ pq$

(97)

fricas

test(i3=1/trace(p*q)*p*q)

$\label{eq98} \mbox{\rm true}$

(98)

fricas

gbs.2

$\label{eq99}\begin{array}{@{}l} \displaystyle \left[{\%x 4 + \%x 3 +{{\frac{2}{{{�� qp}^{2}}\ mq}}\ \%x 1}-{\frac{1}{{{�� qp}^{2}}\ mq \ mp}}}, \: \right. \ \ \displaystyle \left.{ \begin{array}{@{}l} \displaystyle {{\%x 3}^{2}}+{{\left({{\frac{2}{{{�� qp}^{2}}\ mq}}\ \%x 1}-{\frac{1}{{{�� qp}^{2}}\ mq \ mp}}\right)}\ \%x 3}+ \ \ \displaystyle {{\frac{1}{{{�� qp}^{2}}\ {{mq}^{2}}}}\ {{\%x 1}^{2}}}$

(99)

fricas

-- apparently we need to look for solutions in a larger ring
ex2:=map(x+->interpret(x::InputForm)$InputFormFunctions1(FRAC POLY INT),concat(gbs.2,[%x3-%x4]));

s2:=solve(ex2,[%x1,%x2,%x3,%x4]);

#s2

$\label{eq100}2$

(100)

fricas

-- need this to convert solution back to K
(mp,mq,γqp):K

i2:=represents(map(x+->interpret(rhs(x)::InputForm)$InputFormFunctions1(K),s2.1))$A

$\label{eq101}\begin{array}{@{}l} \displaystyle {{\frac{1}{{\left({2 \ {{�� qp}^{2}}}-{2 \ �� qp}\right)}\ mq \ mp}}\ qp}+ \ \ \displaystyle {{\frac{1}{{\left({2 \ {{�� qp}^{2}}}-{2 \ �� qp}\right)}\ mq \ mp}}\ pq}-{{\frac{1}{{\left({2 \ �� qp}- 2 \right)}\ mq}}\ q}- \ \ \displaystyle {{\frac{1}{{\left({2 \ �� qp}- 2 \right)}\ mp}}\ p}$

(101)

fricas

i2':=represents(map(x+->interpret(rhs(x)::InputForm)$InputFormFunctions1(K),s2.2))$A

$\label{eq102}\begin{array}{@{}l} \displaystyle {{\frac{1}{{\left({2 \ {{�� qp}^{2}}}+{2 \ �� qp}\right)}\ mq \ mp}}\ qp}+ \ \ \displaystyle {{\frac{1}{{\left({2 \ {{�� qp}^{2}}}+{2 \ �� qp}\right)}\ mq \ mp}}\ pq}+{{\frac{1}{{\left({2 \ �� qp}+ 2 \right)}\ mq}}\ q}+ \ \ \displaystyle {{\frac{1}{{\left({2 \ �� qp}+ 2 \right)}\ mp}}\ p}$

(102)

fricas

test(n=i2+i2')

$\label{eq103} \mbox{\rm true}$

(103)

fricas

i2*i2'

$\label{eq104}0$

(104)

fricas

i2'*i2

$\label{eq105}0$

(105)

fricas

-- decomposition
i2*x

$\label{eq106}\begin{array}{@{}l} \displaystyle {{\frac{- x 1 +{�� qp \ mq \ x 4}}{2 \ �� qp \ mq}}\ qp}+ \ \ \displaystyle {{\frac{- x 2 +{�� qp \ mp \ x 3}}{2 \ �� qp \ mp}}\ pq}+{{\frac{x 2 -{�� qp \ mp \ x 3}}{2}}\ q}+ \ \ \displaystyle {{\frac{x 1 -{�� qp \ mq \ x 4}}{2}}\ p}$

(106)

fricas

i2'*x

$\label{eq107}\begin{array}{@{}l} \displaystyle {{\frac{x 1 +{�� qp \ mq \ x 4}}{2 \ �� qp \ mq}}\ qp}+ \ \ \displaystyle {{\frac{x 2 +{�� qp \ mp \ x 3}}{2 \ �� qp \ mp}}\ pq}+{{\frac{x 2 +{�� qp \ mp \ x 3}}{2}}\ q}+ \ \ \displaystyle {{\frac{x 1 +{�� qp \ mq \ x 4}}{2}}\ p}$

(107)

fricas

test(i2*p+i2'*p=p)

$\label{eq108} \mbox{\rm true}$

(108)

fricas

test(i2*q+i2'*q=q)

$\label{eq109} \mbox{\rm true}$

(109)

fricas

test(i2*(p*q)+i2'*(p*q)=p*q)

$\label{eq110} \mbox{\rm true}$

(110)

fricas

test(i2*(q*p)+i2'*(q*p)=q*p)

$\label{eq111} \mbox{\rm true}$

(111)

fricas

expr2:=map(x+->interpret(x::InputForm)$InputFormFunctions1(EXPR INT)=0,concat(gbs.2,[]));

s2b:=solve(expr2,[%x1,%x2,%x3]);

#s2b

$\label{eq112}2$

(112)

fricas

s2b.1

$\label{eq113}\begin{array}{@{}l} \displaystyle \left[{ \begin{array}{@{}l} \displaystyle \%x 1 = \ \ \displaystyle {\frac{{\sqrt{-{{{\%x 4}^{2}}\ {{mp}^{2}}\ {{mq}^{2}}\ {{�� qp}^{2}}}+{{{\%x 4}^{2}}\ {{mp}^{2}}\ {{mq}^{2}}}+{\%x 4 \ mp \ mq}}}-{\%x 4 \ mp \ mq}}{mp}}$

(113)

fricas

s2b.2

$\label{eq114}\begin{array}{@{}l} \displaystyle \left[{ \begin{array}{@{}l} \displaystyle \%x 1 = \ \ \displaystyle {\frac{-{\sqrt{-{{{\%x 4}^{2}}\ {{mp}^{2}}\ {{mq}^{2}}\ {{�� qp}^{2}}}+{{{\%x 4}^{2}}\ {{mp}^{2}}\ {{mq}^{2}}}+{\%x 4 \ mp \ mq}}}-{\%x 4 \ mp \ mq}}{mp}}$

(114)

fricas

gbs.1

$\label{eq115}\begin{array}{@{}l} \displaystyle \left[{ \begin{array}{@{}l} \displaystyle \%x 4 + \%x 3 +{{\frac{1}{{{�� qp}^{2}}\ mp}}\ \%x 2}+{{\frac{1}{{{�� qp}^{2}}\ mq}}\ \%x 1}- \ \ \displaystyle {\frac{1}{{{�� qp}^{2}}\ mq \ mp}}$

(115)

fricas

s1:=solve(concat(gbs.1,[%x1-m('p)/trace(P),%x2-m('q)/trace(P)]));

   >> Error detected within library code:
   factor for this domain is unimplemented

fricas

)set output tex off

fricas

)set output algebra on

fricas

expr1a:=map(x+->interpret(x::InputForm)$InputFormFunctions1(EXPR INT)=0,concat(gbs.1,[]));

solve(expr1a,[%x1,%x2])

   (142)
   [
     [
         %x1
       = 
             ROOT
                      2                  2   2  2   4
                  (%x4  + 2 %x3 %x4 + %x3 )mp mq γqp
                + 
                                 2  2                             2
                  (- 4 %x3 %x4 mp mq  + (- 2 %x4 - 2 %x3)mp mq)γqp  + 1
           + 
                                   2
             (- %x4 - %x3)mp mq γqp  + 1
        /
           2 mp
       ,

         %x2
       = 
             -
                ROOT
                         2                  2   2  2   4
                     (%x4  + 2 %x3 %x4 + %x3 )mp mq γqp
                   + 
                                    2  2                             2
                     (- 4 %x3 %x4 mp mq  + (- 2 %x4 - 2 %x3)mp mq)γqp  + 1
           + 
                                   2
             (- %x4 - %x3)mp mq γqp  + 1
        /
           2 mq
       ]
     ,

     [
         %x1
       = 
             -
                ROOT
                         2                  2   2  2   4
                     (%x4  + 2 %x3 %x4 + %x3 )mp mq γqp
                   + 
                                    2  2                             2
                     (- 4 %x3 %x4 mp mq  + (- 2 %x4 - 2 %x3)mp mq)γqp  + 1
           + 
                                   2
             (- %x4 - %x3)mp mq γqp  + 1
        /
           2 mp
       ,

         %x2
       = 
             ROOT
                      2                  2   2  2   4
                  (%x4  + 2 %x3 %x4 + %x3 )mp mq γqp
                + 
                                 2  2                             2
                  (- 4 %x3 %x4 mp mq  + (- 2 %x4 - 2 %x3)mp mq)γqp  + 1
           + 
                                   2
             (- %x4 - %x3)mp mq γqp  + 1
        /
           2 mq
       ]
     ]

expr1b:=map(x+->interpret(x::InputForm)$InputFormFunctions1(EXPR INT)=0,concat(gbs.1,[%x3-%x4]));

solve(expr1b,[%x1,%x2,%x3])

   (144)
   [
     [
         %x1
       = 
                +---------------------------------------------------------+
                |     2  2  2   4           2  2  2                  2
             - \|4 %x4 mp mq γqp  + (- 4 %x4 mp mq  - 4 %x4 mp mq)γqp  + 1
           + 
                              2
             - 2 %x4 mp mq γqp  + 1
        /
           2 mp
       ,

         %x2
       = 
              +---------------------------------------------------------+
              |     2  2  2   4           2  2  2                  2
             \|4 %x4 mp mq γqp  + (- 4 %x4 mp mq  - 4 %x4 mp mq)γqp  + 1
           + 
                              2
             - 2 %x4 mp mq γqp  + 1
        /
           2 mq
       ,
      %x3 = %x4]
     ,

     [
         %x1
       = 
              +---------------------------------------------------------+
              |     2  2  2   4           2  2  2                  2
             \|4 %x4 mp mq γqp  + (- 4 %x4 mp mq  - 4 %x4 mp mq)γqp  + 1
           + 
                              2
             - 2 %x4 mp mq γqp  + 1
        /
           2 mp
       ,

         %x2
       = 
                +---------------------------------------------------------+
                |     2  2  2   4           2  2  2                  2
             - \|4 %x4 mp mq γqp  + (- 4 %x4 mp mq  - 4 %x4 mp mq)γqp  + 1
           + 
                              2
             - 2 %x4 mp mq γqp  + 1
        /
           2 mq
       ,
      %x3 = %x4]
     ]