(the maths inside is not meant to be taken seriously;
'tis a silly idea that can't work)
Note that dropping comutativity below we get quantum probablility.
Franz Lehner added packages supporting computations for several
popular versions. In principle one can treat commutative
case as a special case of quantum probablility...
from a recent email by Peter Broadbery
Random variables are assumed to have the following properties:
- complex constants are random variables;
- the sum of two random variables is a random variable;
- the product of two random variables is a random variable;
- addition and multiplication of random variables are both commutative; and
- there is a notion of conjugation of random variables, satisfying:
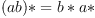 and
and 
for all random variables 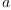 ,
, 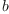 , and coinciding with complex conjugation
if
, and coinciding with complex conjugation
if 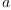 is a constant.
is a constant.
This means that random variables form complex abelian  -algebras. If
-algebras. If 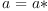 ,
the random variable a is called "real".
,
the random variable a is called "real".
An expectation E on an algebra A of random variables is a normalized, positive
linear functional. What this means is that
-
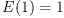 ;
;
-
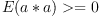 for all random variables
for all random variables 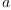 ;
;
-
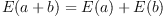 for all random variables
for all random variables 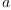 and
and 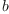 ; and
; and
-
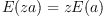 if
if 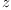 is a constant.
is a constant.
 -algebra
-algebra
From Wikipedia, the free encyclopedia
In mathematics, a  -algebra is an associative algebra over the field of
complex numbers with an antilinear, antiautomorphism
-algebra is an associative algebra over the field of
complex numbers with an antilinear, antiautomorphism 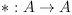 which is an
involution. More precisely,
which is an
involution. More precisely,  is required to satisfy the following properties:
is required to satisfy the following properties:
for all 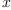 ,
,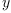 in
in 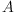 , and all
, and all 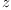 in
in 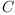 .
.
The most obvious example of a  -algebra is the field of complex numbers C
where
-algebra is the field of complex numbers C
where  is just complex conjugation. Another example is the algebra of nn
matrices over
is just complex conjugation. Another example is the algebra of nn
matrices over 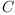 with
with  given by the conjugate transpose.
given by the conjugate transpose.
An algebra homomorphism 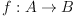 is a
is a  -homomorphism if it is compatible
with the involutions of
-homomorphism if it is compatible
with the involutions of 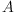 and
and 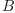 , i.e.
, i.e.
An element 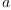 in
in 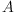 is called self-adjoint if
is called self-adjoint if 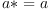 .
.
fricas
(1) -> <aldor>
#include "fricas"
RandomAlgebra(F: Field): Category == with {
Algebra F;
E: % -> F;
sample: % -> F;
}
local PolyHelper(F: Field): with {
expand: SparseUnivariatePolynomial F -> Generator Cross(F, NonNegativeInteger);
}
== add {
expand(p: SparseUnivariatePolynomial F): Generator Cross(F, NonNegativeInteger) == generate {
default m: SparseUnivariatePolynomial F;
import from SparseUnivariatePolynomial F;
import from List SparseUnivariatePolynomial F;
for m in monomials p repeat {
yield (leadingCoefficient m, degree m);
}
}
}
UnivariateNormalRandomAlgebra: RandomAlgebra Float with {
X: () -> %;
variance: % -> Float;
} == add {
Rep ==> SparseUnivariatePolynomial Float;
import from Rep;
0: % == per 0;
1: % == per 1;
X(): % == per(monomial(1$Float,1$NonNegativeInteger)$Rep);
characteristic(): NonNegativeInteger == 0;
-(x: %): % == per(-rep x);
(a: %) = (b: %): Boolean == rep(a) = rep(b);
(a: %) + (b: %): % == per(rep(a) + rep(b));
(a: %) * (b: %): % == per(rep(a) * rep(b));
(a: Float) * (b: %): % == per(a * rep(b));
coerce(x: Integer): % == per(x::Rep);
coerce(x: Float): % == per(x::Rep);
coerce(x: %): OutputForm == coerce rep(x);
E(X: %): Float == {
import from PolyHelper Float;
z: Float := 0;
for p in expand rep(X) repeat {
(a, b) := p;
z := z + a * E(b);
}
z
}
-- should be a random sampling of x.
sample(X: %): Float == {
import from PolyHelper Float;
import from Float;
u := uniform01()$RandomFloatDistributions;
x: Float := 0;
for p in expand rep(X) repeat {
(a, b) := p;
x := x + a * u^b;
}
return x;
}
variance(X: %): Float == { A := (X-E(X)*1); E(A*A); }
-- return expected value of X^n
local E(n: NonNegativeInteger): Float == {
p: Rep := 1;
-- yuck. There must be a nicer way than this..
for i in 1..n repeat p := differentiate(p) + monomial(1,1)*p;
coefficient(p,0);
}
}</aldor>
fricas
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/5264249576821309342-25px001.as
using Aldor compiler and options
-O -Fasy -Fao -Flsp -lfricas -Mno-ALDOR_W_WillObsolete -DFriCAS -Y $FRICAS/algebra -I $FRICAS/algebra
Use the system command )set compiler args to change these
options.fricas
Compiling Lisp source code from file
./5264249576821309342-25px001.lsp
Issuing )library command for 5264249576821309342-25px001fricas
Reading #P"/var/aw/var/LatexWiki/5264249576821309342-25px001.asy"
RandomAlgebra is now explicitly exposed in frame initial
>> System error:
The function BOOT::ASHARPMKAUTOLOADFUNCTOR is undefined.
fricas
a := X()$UnivariateNormalRandomAlgebra
UnivariateNormalRandomAlgebra is not a valid type.