Consider the following function, given in recursive manner:
fricas
(1) -> N0(t|(t<0) or (t>1))==0
Type: Void
fricas
N0(t|(t>=0) and (t<=1))==1
Type: Void
fricas
N(t,i,0)==N0(t-i)
Type: Void
fricas
N(t,i,p|p>0)==(t-i)/p*N(t,i,p-1)+(i+1-t)/p*N(t,i+1,p-1)
Type: Void
This is a way to create (uniform) bsplines. Now try to differentiate 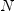
fricas
D(N(t,0,3),t)
There are 3 exposed and 1 unexposed library operations named <
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op <
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named <
with argument type(s)
Polynomial(Integer)
NonNegativeInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
There are 3 exposed and 1 unexposed library operations named <
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op <
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named <
with argument type(s)
Polynomial(Integer)
NonNegativeInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
There are 3 exposed and 1 unexposed library operations named <
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op <
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named <
with argument type(s)
Polynomial(Integer)
NonNegativeInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
Yack!!! This does not work. The map
is
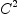
continuous,
but
FriCAS only has
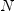
defined as code. There is no order on expressions
so this can not work (as we see below).
fricas
N(t,0,3)
There are 3 exposed and 1 unexposed library operations named <
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op <
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named <
with argument type(s)
Polynomial(Integer)
NonNegativeInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
There are 3 exposed and 1 unexposed library operations named <
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op <
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named <
with argument type(s)
Polynomial(Integer)
NonNegativeInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
On the other hand the function can be evaluated for specific numerial arguments.
See this:
fricas
N0(t|(t<0) or (t>1))==0;
Compiled code for N0 has been cleared.
Compiled code for N has been cleared.
1 old definition(s) deleted for function or rule N0
Type: Void
fricas
N0(t|(t>=0) and (t<=1))==1;
1 old definition(s) deleted for function or rule N0
Type: Void
fricas
N(t,i,0)==N0(t-i);
1 old definition(s) deleted for function or rule N
Type: Void
fricas
N(t,i,p|p>0)==(t-i)/p*N(t,i,p-1)+(i+1-t)/p*N(t,i+1,p-1);
1 old definition(s) deleted for function or rule N
Type: Void
fricas
for x in -5..15 repeat output N(x/10,0,3)
fricas
Compiling function N0 with type Fraction(Integer) ->
NonNegativeIntegerfricas
Compiling function N with type (Fraction(Integer), Integer, Integer)
-> Fraction(Integer)
0
0
0
0
0
0
1
----
6000
1
---
750
9
----
2000
4
---
375
1
--
48
9
---
250
343
----
6000
32
---
375
243
----
2000
1
-
6
133
- ----
6000
43
- ---
750
217
- ----
2000
67
- ---
375
13
- --
48
Type: Void
Drawing the plot (unfortunately not available here) would
show it even more clearly.
But in D(N(t,0,3),t) you are not calling the function N
with numeric parameters. In N(t,0,3) the type of t is
Variable t. Ultimately N(t,0,3) fails because of your function
definition N0(t|(t<0) or (t>1))==0. This is because
t>1 fails. Namely, FriCAS interprets both t and 1 as being of type POLY INT
and there is no order on the polynomials. You can
see why if you use the option )set message bottomup on to
see the mode map selection
fricas
)set message bottomup on
Your user access level is compiler and this set option is therefore
not available. See the )set userlevel command for more
information.
t>1
There are 1 exposed and 2 unexposed library operations named >
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op >
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named >
with argument type(s)
Variable(t)
PositiveInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
This result is counter-intuitive for people expecting symbolic computation,
but once you understand why
FriCAS handles this as above then you will be in a good position to
understand the rest of FriCAS type system!
It is possible to write the function N0 so that it returns the
desired result (using abs).