MathAction Octonion Algebra is Frobenius in Just One Way

Topics

FrontPage
- FriCASContributions
  - Frobenius Algebra, Vector Spaces and Polynomial Ideals
    - Octonion Algebra is Frobenius in Just One Way <-- You are here.

Octonion Algebra Is Frobenius In Just One Way

Linear operators over a 8-dimensional vector space representing octonnion algebra

Ref:

http://arxiv.org/abs/1103.5113
-permuted Frobenius Algebras

Zbigniew Oziewicz (UNAM), Gregory Peter Wene (UTSA)
http://mat.uab.es/~kock/TQFT.html
Frobenius algebras and 2D topological quantum field theories

Joachim Kock
http://en.wikipedia.org/wiki/Frobenius_algebra
http://en.wikipedia.org/wiki/Octonion

We need the Axiom LinearOperator library.

fricas

)library CARTEN ARITY CMONAL CPROP CLOP CALEY

   CartesianTensor is now explicitly exposed in frame initial 
   CartesianTensor will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/CARTEN.NRLIB/CARTEN
   Arity is now explicitly exposed in frame initial 
   Arity will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/ARITY.NRLIB/ARITY
   ClosedMonoidal is now explicitly exposed in frame initial 
   ClosedMonoidal will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/CMONAL.NRLIB/CMONAL
   ClosedProp is now explicitly exposed in frame initial 
   ClosedProp will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/CPROP.NRLIB/CPROP
   ClosedLinearOperator is now explicitly exposed in frame initial 
   ClosedLinearOperator will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/CLOP.NRLIB/CLOP
   CaleyDickson is now explicitly exposed in frame initial 
   CaleyDickson will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/CALEY.NRLIB/CALEY

Use the following macros for convenient notation

fricas

-- summation
macro Σ(x,i,n)==reduce(+,[x for i in n])

Type: Void

fricas

-- subscript
macro sb == subscript

Type: Void

ℒ is the domain of 8-dimensional linear operators over the rational functions ℚ (Expression Integer), i.e. ratio of polynomials with integer coefficients.

fricas

dim:=8

$\label{eq1}8$

(1)

Type: PositiveInteger?

fricas

macro ℂ == CaleyDickson

Type: Void

fricas

macro ℚ == Expression Integer

Type: Void

fricas

ℒ := ClosedLinearOperator(OVAR ['0,'1,'2,'3,'4,'5,'6,'7], ℚ)

$\label{eq2}\hbox{\axiomType{ClosedLinearOperator}\ } (\hbox{\axiomType{OrderedVariableList}\ } ([ 0, 1, 2, 3, 4, 5, 6, 7 ]) , \hbox{\axiomType{Expression}\ } (\hbox{\axiomType{Integer}\ }))$

(2)

Type: Type

fricas

ⅇ:List ℒ      := basisOut()

$\label{eq3}\left[{|_{\ 0}}, \:{|_{\ 1}}, \:{|_{\ 2}}, \:{|_{\ 3}}, \:{|_{\ 4}}, \:{|_{\ 5}}, \:{|_{\ 6}}, \:{|_{\ 7}}\right]$

(3)

Type: List(ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer)))

fricas

ⅆ:List ℒ      := basisIn()

$\label{eq4}\left[{|^{\ 0}}, \:{|^{\ 1}}, \:{|^{\ 2}}, \:{|^{\ 3}}, \:{|^{\ 4}}, \:{|^{\ 5}}, \:{|^{\ 6}}, \:{|^{\ 7}}\right]$

(4)

Type: List(ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer)))

fricas

I:ℒ:=[1];   -- identity for composition

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

X:ℒ:=[2,1]; -- twist

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

V:ℒ:=ev(1) -- evaluation

$\label{eq5}{|^{\ 0 \ 0}}+{|^{\ 1 \ 1}}+{|^{\ 2 \ 2}}+{|^{\ 3 \ 3}}+{|^{\ 4 \ 4}}+{|^{\ 5 \ 5}}+{|^{\ 6 \ 6}}+{|^{\ 7 \ 7}}$

(5)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

Λ:ℒ:=co(1) -- co-evaluation

$\label{eq6}{|_{\ 0 \ 0}}+{|_{\ 1 \ 1}}+{|_{\ 2 \ 2}}+{|_{\ 3 \ 3}}+{|_{\ 4 \ 4}}+{|_{\ 5 \ 5}}+{|_{\ 6 \ 6}}+{|_{\ 7 \ 7}}$

(6)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

Now generate structure constants for Octonion Algebra

The basis consists of the real and imaginary units. We use quaternion multiplication to form the "multiplication table" as a matrix. Then the structure constants can be obtained by dividing each matrix entry by the list of basis vectors.

Split-complex, co-quaternions and split-octonions can be specified by Caley-Dickson parameters

fricas

--q0:=sb('q,[0])
q0:=1  -- not split-complex

$\label{eq7}1$

(7)

Type: PositiveInteger?

fricas

--q1:=sb('q,[1])
q1:=1  -- not co-quaternion

$\label{eq8}1$

(8)

Type: PositiveInteger?

fricas

q2:=sb('q,[2])

$\label{eq9}q_{2}$

(9)

Type: Symbol

fricas

--q2:=1  -- split-octonion
QQ := ℂ(ℂ(ℂ(ℚ,'i,q0),'j,q1),'k,q2);

Type: Type

Basis: Each B.i is a octonion number

fricas

B:List QQ := map(x +-> hyper x,1$SQMATRIX(dim,ℚ)::List List ℚ)

$\label{eq10}\left[ 1, \: i , \: j , \:{ij}, \: k , \:{ik}, \:{jk}, \:{{ij}k}\right]$

(10)

Type: List(CaleyDickson(CaleyDickson(CaleyDickson(Expression(Integer),i,1),j,1),k,q[2]))

fricas

-- Multiplication table:
M:Matrix QQ := matrix [[B.i*B.j for i in 1..dim] for j in 1..dim]

$\label{eq11}\left[ \begin{array}{cccccccc} 1 & i & j &{ij}& k &{ik}&{jk}&{{ij}k} \ i & - 1 & -{ij}& j &{- ik}& k &{{ij}k}& -{jk} \ j &{ij}& - 1 & - i & -{jk}&{-{ij}k}& k &{ik} \ {ij}& - j & i & - 1 &{-{ij}k}&{jk}&{- ik}& k \ k &{ik}&{jk}&{{ij}k}& -{q_{2}}&{-{q_{2}}i}&{-{q_{2}}j}&{{-{\overline{q_{2}}}i}j} \ {ik}& - k &{{ij}k}& -{jk}&{{q_{2}}i}& -{q_{2}}&{{{q_{2}}i}j}&{-{\overline{q_{2}}}j} \ {jk}&{-{ij}k}& - k &{ik}&{{q_{2}}j}&{{-{q_{2}}i}j}& -{q_{2}}&{{\overline{q_{2}}}i} \ {{ij}k}&{jk}&{- ik}& - k &{{{\overline{q_{2}}}i}j}&{{\overline{q_{2}}}j}&{-{\overline{q_{2}}}i}& -{q_{2}}$

(11)

Type: Matrix(CaleyDickson(CaleyDickson(CaleyDickson(Expression(Integer),i,1),j,1),k,q[2]))

fricas

-- Function to divide the matrix entries by a basis element
S(y) == map(x +-> real real real(x/y),M)

Type: Void

fricas

-- The result is a nested list
ѕ :=map(S,B)::List List List ℚ;

fricas

Compiling function S with type CaleyDickson(CaleyDickson(
      CaleyDickson(Expression(Integer),i,1),j,1),k,q[2]) -> Matrix(
      Expression(Integer))

Type: List(List(List(Expression(Integer))))

fricas

-- structure constants form a tensor operator
Y := Σ(Σ(Σ(ѕ(i)(k)(j)*ⅇ.i*ⅆ.j*ⅆ.k, i,1..dim), j,1..dim), k,1..dim)

$\label{eq12}\begin{array}{@{}l} \displaystyle {|_{\ 0}^{\ 0 \ 0}}+{|_{\ 1}^{\ 0 \ 1}}+{|_{\ 2}^{\ 0 \ 2}}+{|_{\ 3}^{\ 0 \ 3}}+{{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 0 \ 4}}}+{|_{\ 5}^{\ 0 \ 5}}+ \ \ \displaystyle {|_{\ 6}^{\ 0 \ 6}}+{|_{\ 7}^{\ 0 \ 7}}+{|_{\ 1}^{\ 1 \ 0}}-{|_{\ 0}^{\ 1 \ 1}}+{|_{\ 3}^{\ 1 \ 2}}-{|_{\ 2}^{\ 1 \ 3}}+ \ \ \displaystyle {|_{\ 5}^{\ 1 \ 4}}-{{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 1 \ 5}}}-{|_{\ 7}^{\ 1 \ 6}}+{|_{\ 6}^{\ 1 \ 7}}+{|_{\ 2}^{\ 2 \ 0}}-{|_{\ 3}^{\ 2 \ 1}}- \ \ \displaystyle {|_{\ 0}^{\ 2 \ 2}}+{|_{\ 1}^{\ 2 \ 3}}+{|_{\ 6}^{\ 2 \ 4}}+{|_{\ 7}^{\ 2 \ 5}}-{{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 2 \ 6}}}-{|_{\ 5}^{\ 2 \ 7}}+ \ \ \displaystyle {|_{\ 3}^{\ 3 \ 0}}+{|_{\ 2}^{\ 3 \ 1}}-{|_{\ 1}^{\ 3 \ 2}}-{|_{\ 0}^{\ 3 \ 3}}+{|_{\ 7}^{\ 3 \ 4}}-{|_{\ 6}^{\ 3 \ 5}}+ \ \ \displaystyle {|_{\ 5}^{\ 3 \ 6}}-{{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 3 \ 7}}}+{{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 4 \ 0}}}-{|_{\ 5}^{\ 4 \ 1}}-{|_{\ 6}^{\ 4 \ 2}}-{|_{\ 7}^{\ 4 \ 3}}- \ \ \displaystyle {{q_{2}}\ {|_{\ 0}^{\ 4 \ 4}}}+{{q_{2}}\ {|_{\ 1}^{\ 4 \ 5}}}+{{q_{2}}\ {|_{\ 2}^{\ 4 \ 6}}}+{{q_{2}}\ {|_{\ 3}^{\ 4 \ 7}}}+{|_{\ 5}^{\ 5 \ 0}}+ \ \ \displaystyle {{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 5 \ 1}}}-{|_{\ 7}^{\ 5 \ 2}}+{|_{\ 6}^{\ 5 \ 3}}-{{q_{2}}\ {|_{\ 1}^{\ 5 \ 4}}}-{{q_{2}}\ {|_{\ 0}^{\ 5 \ 5}}}- \ \ \displaystyle {{\overline{q_{2}}}\ {|_{\ 3}^{\ 5 \ 6}}}+{{\overline{q_{2}}}\ {|_{\ 2}^{\ 5 \ 7}}}+{|_{\ 6}^{\ 6 \ 0}}+{|_{\ 7}^{\ 6 \ 1}}+{{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 6 \ 2}}}- \ \ \displaystyle {|_{\ 5}^{\ 6 \ 3}}-{{q_{2}}\ {|_{\ 2}^{\ 6 \ 4}}}+{{\overline{q_{2}}}\ {|_{\ 3}^{\ 6 \ 5}}}-{{q_{2}}\ {|_{\ 0}^{\ 6 \ 6}}}-{{\overline{q_{2}}}\ {|_{\ 1}^{\ 6 \ 7}}}+ \ \ \displaystyle {|_{\ 7}^{\ 7 \ 0}}-{|_{\ 6}^{\ 7 \ 1}}+{|_{\ 5}^{\ 7 \ 2}}+{{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 7 \ 3}}}-{{q_{2}}\ {|_{\ 3}^{\ 7 \ 4}}}- \ \ \displaystyle {{\overline{q_{2}}}\ {|_{\ 2}^{\ 7 \ 5}}}+{{\overline{q_{2}}}\ {|_{\ 1}^{\ 7 \ 6}}}-{{q_{2}}\ {|_{\ 0}^{\ 7 \ 7}}}$

(12)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

arity Y

$\label{eq13}{{+}^{2}}\over +$

(13)

Type: ClosedProp?(ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer)))

fricas

matrix [[(ⅇ.i*ⅇ.j)/Y for i in 1..dim] for j in 1..dim]

$\label{eq14}\left[ \begin{array}{cccccccc} {|_{\ 0}}&{|_{\ 1}}&{|_{\ 2}}&{|_{\ 3}}&{{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}}}&{|_{\ 5}}&{|_{\ 6}}&{|_{\ 7}} \ {|_{\ 1}}& -{|_{\ 0}}& -{|_{\ 3}}&{|_{\ 2}}& -{|_{\ 5}}&{{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}}}&{|_{\ 7}}& -{|_{\ 6}} \ {|_{\ 2}}&{|_{\ 3}}& -{|_{\ 0}}& -{|_{\ 1}}& -{|_{\ 6}}& -{|_{\ 7}}&{{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}}}&{|_{\ 5}} \ {|_{\ 3}}& -{|_{\ 2}}&{|_{\ 1}}& -{|_{\ 0}}& -{|_{\ 7}}&{|_{\ 6}}& -{|_{\ 5}}&{{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}}} \ {{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}}}&{|_{\ 5}}&{|_{\ 6}}&{|_{\ 7}}& -{{q_{2}}\ {|_{\ 0}}}& -{{q_{2}}\ {|_{\ 1}}}& -{{q_{2}}\ {|_{\ 2}}}& -{{q_{2}}\ {|_{\ 3}}} \ {|_{\ 5}}& -{{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}}}&{|_{\ 7}}& -{|_{\ 6}}&{{q_{2}}\ {|_{\ 1}}}& -{{q_{2}}\ {|_{\ 0}}}&{{\overline{q_{2}}}\ {|_{\ 3}}}& -{{\overline{q_{2}}}\ {|_{\ 2}}} \ {|_{\ 6}}& -{|_{\ 7}}& -{{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}}}&{|_{\ 5}}&{{q_{2}}\ {|_{\ 2}}}& -{{\overline{q_{2}}}\ {|_{\ 3}}}& -{{q_{2}}\ {|_{\ 0}}}&{{\overline{q_{2}}}\ {|_{\ 1}}} \ {|_{\ 7}}&{|_{\ 6}}& -{|_{\ 5}}& -{{{q_{2}}\over{\overline{q_{2}}}}\ {|_{\ 4}}}&{{q_{2}}\ {|_{\ 3}}}&{{\overline{q_{2}}}\ {|_{\ 2}}}& -{{\overline{q_{2}}}\ {|_{\ 1}}}& -{{q_{2}}\ {|_{\ 0}}}$

(14)

Type: Matrix(ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer)))

A scalar product is denoted by the (2,0)-tensor $U = \{ u_{ij} \}$

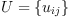
fricas

U:=Σ(Σ(script('u,[[],[i,j]])*ⅆ.i*ⅆ.j, i,1..dim), j,1..dim)

$\label{eq15}\begin{array}{@{}l} \displaystyle {{u^{1, \: 1}}\ {|^{\ 0 \ 0}}}+{{u^{1, \: 2}}\ {|^{\ 0 \ 1}}}+{{u^{1, \: 3}}\ {|^{\ 0 \ 2}}}+{{u^{1, \: 4}}\ {|^{\ 0 \ 3}}}+ \ \ \displaystyle {{u^{1, \: 5}}\ {|^{\ 0 \ 4}}}+{{u^{1, \: 6}}\ {|^{\ 0 \ 5}}}+{{u^{1, \: 7}}\ {|^{\ 0 \ 6}}}+{{u^{1, \: 8}}\ {|^{\ 0 \ 7}}}+ \ \ \displaystyle {{u^{2, \: 1}}\ {|^{\ 1 \ 0}}}+{{u^{2, \: 2}}\ {|^{\ 1 \ 1}}}+{{u^{2, \: 3}}\ {|^{\ 1 \ 2}}}+{{u^{2, \: 4}}\ {|^{\ 1 \ 3}}}+ \ \ \displaystyle {{u^{2, \: 5}}\ {|^{\ 1 \ 4}}}+{{u^{2, \: 6}}\ {|^{\ 1 \ 5}}}+{{u^{2, \: 7}}\ {|^{\ 1 \ 6}}}+{{u^{2, \: 8}}\ {|^{\ 1 \ 7}}}+ \ \ \displaystyle {{u^{3, \: 1}}\ {|^{\ 2 \ 0}}}+{{u^{3, \: 2}}\ {|^{\ 2 \ 1}}}+{{u^{3, \: 3}}\ {|^{\ 2 \ 2}}}+{{u^{3, \: 4}}\ {|^{\ 2 \ 3}}}+ \ \ \displaystyle {{u^{3, \: 5}}\ {|^{\ 2 \ 4}}}+{{u^{3, \: 6}}\ {|^{\ 2 \ 5}}}+{{u^{3, \: 7}}\ {|^{\ 2 \ 6}}}+{{u^{3, \: 8}}\ {|^{\ 2 \ 7}}}+ \ \ \displaystyle {{u^{4, \: 1}}\ {|^{\ 3 \ 0}}}+{{u^{4, \: 2}}\ {|^{\ 3 \ 1}}}+{{u^{4, \: 3}}\ {|^{\ 3 \ 2}}}+{{u^{4, \: 4}}\ {|^{\ 3 \ 3}}}+ \ \ \displaystyle {{u^{4, \: 5}}\ {|^{\ 3 \ 4}}}+{{u^{4, \: 6}}\ {|^{\ 3 \ 5}}}+{{u^{4, \: 7}}\ {|^{\ 3 \ 6}}}+{{u^{4, \: 8}}\ {|^{\ 3 \ 7}}}+ \ \ \displaystyle {{u^{5, \: 1}}\ {|^{\ 4 \ 0}}}+{{u^{5, \: 2}}\ {|^{\ 4 \ 1}}}+{{u^{5, \: 3}}\ {|^{\ 4 \ 2}}}+{{u^{5, \: 4}}\ {|^{\ 4 \ 3}}}+ \ \ \displaystyle {{u^{5, \: 5}}\ {|^{\ 4 \ 4}}}+{{u^{5, \: 6}}\ {|^{\ 4 \ 5}}}+{{u^{5, \: 7}}\ {|^{\ 4 \ 6}}}+{{u^{5, \: 8}}\ {|^{\ 4 \ 7}}}+ \ \ \displaystyle {{u^{6, \: 1}}\ {|^{\ 5 \ 0}}}+{{u^{6, \: 2}}\ {|^{\ 5 \ 1}}}+{{u^{6, \: 3}}\ {|^{\ 5 \ 2}}}+{{u^{6, \: 4}}\ {|^{\ 5 \ 3}}}+ \ \ \displaystyle {{u^{6, \: 5}}\ {|^{\ 5 \ 4}}}+{{u^{6, \: 6}}\ {|^{\ 5 \ 5}}}+{{u^{6, \: 7}}\ {|^{\ 5 \ 6}}}+{{u^{6, \: 8}}\ {|^{\ 5 \ 7}}}+ \ \ \displaystyle {{u^{7, \: 1}}\ {|^{\ 6 \ 0}}}+{{u^{7, \: 2}}\ {|^{\ 6 \ 1}}}+{{u^{7, \: 3}}\ {|^{\ 6 \ 2}}}+{{u^{7, \: 4}}\ {|^{\ 6 \ 3}}}+ \ \ \displaystyle {{u^{7, \: 5}}\ {|^{\ 6 \ 4}}}+{{u^{7, \: 6}}\ {|^{\ 6 \ 5}}}+{{u^{7, \: 7}}\ {|^{\ 6 \ 6}}}+{{u^{7, \: 8}}\ {|^{\ 6 \ 7}}}+ \ \ \displaystyle {{u^{8, \: 1}}\ {|^{\ 7 \ 0}}}+{{u^{8, \: 2}}\ {|^{\ 7 \ 1}}}+{{u^{8, \: 3}}\ {|^{\ 7 \ 2}}}+{{u^{8, \: 4}}\ {|^{\ 7 \ 3}}}+ \ \ \displaystyle {{u^{8, \: 5}}\ {|^{\ 7 \ 4}}}+{{u^{8, \: 6}}\ {|^{\ 7 \ 5}}}+{{u^{8, \: 7}}\ {|^{\ 7 \ 6}}}+{{u^{8, \: 8}}\ {|^{\ 7 \ 7}}}$

(15)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

Definition 1

We say that the scalar product is associative if the tensor equation holds:

    Y   =   Y
     U     U

In other words, if the (3,0)-tensor:

$\scalebox{1} % Change this value to rescale the drawing. { \begin{pspicture}(0,-0.92)(4.82,0.92) \psbezier[linewidth=0.04](2.2,0.9)(2.2,0.1)(2.6,0.1)(2.6,0.9) \psline[linewidth=0.04cm](2.4,0.3)(2.4,-0.1) \psbezier[linewidth=0.04](2.4,-0.1)(2.4,-0.9)(3.0,-0.9)(3.0,-0.1) \psline[linewidth=0.04cm](3.0,-0.1)(3.0,0.9) \psbezier[linewidth=0.04](4.8,0.9)(4.8,0.1)(4.4,0.1)(4.4,0.9) \psline[linewidth=0.04cm](4.6,0.3)(4.6,-0.1) \psbezier[linewidth=0.04](4.6,-0.1)(4.6,-0.9)(4.0,-0.9)(4.0,-0.1) \psline[linewidth=0.04cm](4.0,-0.1)(4.0,0.9) \usefont{T1}{ptm}{m}{n} \rput(3.4948437,0.205){-} \psline[linewidth=0.04cm](0.6,-0.7)(0.6,0.9) \psbezier[linewidth=0.04](0.0,-0.1)(0.0,-0.9)(1.2,-0.9)(1.2,-0.1) \psline[linewidth=0.04cm](0.0,-0.1)(0.0,0.9) \psline[linewidth=0.04cm](1.2,-0.1)(1.2,0.9) \usefont{T1}{ptm}{m}{n} \rput(1.6948438,0.205){=} \end{pspicture} }$

$\label{eq16} \Phi = \{ \phi^{ijk} = {y^e}_{ij} u_{ek} - u_{ie} {y_e}^{jk} \}$

(16)

(three-point function) is zero.

Using the LinearOperator domain in Axiom and some carefully chosen symbols we can easily enter expressions that are both readable and interpreted by Axiom as "graphical calculus" diagrams describing complex products and compositions of linear operators.

fricas

ω:ℒ :=(Y*I)/U  - (I*Y)/U;

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

Definition 2

An algebra with a non-degenerate associative scalar product is called a [Frobenius Algebra]?.

The Cartan-Killing Trace

fricas

Ú:=
   (  Y Λ  ) / _
   (   Y I ) / _
        V

$\label{eq17}\begin{array}{@{}l} \displaystyle {{{{7 \ {\overline{q_{2}}}}+{q_{2}}}\over{\overline{q_{2}}}}\ {|^{\ 0 \ 0}}}+{{{-{7 \ {\overline{q_{2}}}}-{q_{2}}}\over{\overline{q_{2}}}}\ {|^{\ 1 \ 1}}}+{{{-{7 \ {\overline{q_{2}}}}-{q_{2}}}\over{\overline{q_{2}}}}\ {|^{\ 2 \ 2}}}+ \ \ \displaystyle {{{-{7 \ {\overline{q_{2}}}}-{q_{2}}}\over{\overline{q_{2}}}}\ {|^{\ 3 \ 3}}}+{{{-{7 \ {q_{2}}\ {\overline{q_{2}}}}-{{q_{2}}^{2}}}\over{\overline{q_{2}}}}\ {|^{\ 4 \ 4}}}+ \ \ \displaystyle {{{-{7 \ {q_{2}}\ {\overline{q_{2}}}}-{{q_{2}}^{2}}}\over{\overline{q_{2}}}}\ {|^{\ 5 \ 5}}}+{{{-{7 \ {q_{2}}\ {\overline{q_{2}}}}-{{q_{2}}^{2}}}\over{\overline{q_{2}}}}\ {|^{\ 6 \ 6}}}+ \ \ \displaystyle {{{-{7 \ {q_{2}}\ {\overline{q_{2}}}}-{{q_{2}}^{2}}}\over{\overline{q_{2}}}}\ {|^{\ 7 \ 7}}}$

(17)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

Ù:=
   (  Λ Y  ) / _
   ( I Y   ) / _
      V

$\label{eq18}\begin{array}{@{}l} \displaystyle {{{{7 \ {\overline{q_{2}}}}+{q_{2}}}\over{\overline{q_{2}}}}\ {|^{\ 0 \ 0}}}+{{{-{7 \ {\overline{q_{2}}}}-{q_{2}}}\over{\overline{q_{2}}}}\ {|^{\ 1 \ 1}}}+{{{-{7 \ {\overline{q_{2}}}}-{q_{2}}}\over{\overline{q_{2}}}}\ {|^{\ 2 \ 2}}}+ \ \ \displaystyle {{{-{7 \ {\overline{q_{2}}}}-{q_{2}}}\over{\overline{q_{2}}}}\ {|^{\ 3 \ 3}}}+{{{-{7 \ {q_{2}}\ {\overline{q_{2}}}}-{{q_{2}}^{2}}}\over{\overline{q_{2}}}}\ {|^{\ 4 \ 4}}}+ \ \ \displaystyle {{{-{7 \ {q_{2}}\ {\overline{q_{2}}}}-{{q_{2}}^{2}}}\over{\overline{q_{2}}}}\ {|^{\ 5 \ 5}}}+{{{-{7 \ {q_{2}}\ {\overline{q_{2}}}}-{{q_{2}}^{2}}}\over{\overline{q_{2}}}}\ {|^{\ 6 \ 6}}}+ \ \ \displaystyle {{{-{7 \ {q_{2}}\ {\overline{q_{2}}}}-{{q_{2}}^{2}}}\over{\overline{q_{2}}}}\ {|^{\ 7 \ 7}}}$

(18)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

test(Ù=Ú)

$\label{eq19} \mbox{\rm true}$

(19)

Type: Boolean

forms a non-degenerate associative scalar product for Y

fricas

Ũ := Ù

$\label{eq20}\begin{array}{@{}l} \displaystyle {{{{7 \ {\overline{q_{2}}}}+{q_{2}}}\over{\overline{q_{2}}}}\ {|^{\ 0 \ 0}}}+{{{-{7 \ {\overline{q_{2}}}}-{q_{2}}}\over{\overline{q_{2}}}}\ {|^{\ 1 \ 1}}}+{{{-{7 \ {\overline{q_{2}}}}-{q_{2}}}\over{\overline{q_{2}}}}\ {|^{\ 2 \ 2}}}+ \ \ \displaystyle {{{-{7 \ {\overline{q_{2}}}}-{q_{2}}}\over{\overline{q_{2}}}}\ {|^{\ 3 \ 3}}}+{{{-{7 \ {q_{2}}\ {\overline{q_{2}}}}-{{q_{2}}^{2}}}\over{\overline{q_{2}}}}\ {|^{\ 4 \ 4}}}+ \ \ \displaystyle {{{-{7 \ {q_{2}}\ {\overline{q_{2}}}}-{{q_{2}}^{2}}}\over{\overline{q_{2}}}}\ {|^{\ 5 \ 5}}}+{{{-{7 \ {q_{2}}\ {\overline{q_{2}}}}-{{q_{2}}^{2}}}\over{\overline{q_{2}}}}\ {|^{\ 6 \ 6}}}+ \ \ \displaystyle {{{-{7 \ {q_{2}}\ {\overline{q_{2}}}}-{{q_{2}}^{2}}}\over{\overline{q_{2}}}}\ {|^{\ 7 \ 7}}}$

(20)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

test
     (    Y I    )  /
           Ũ        =
     (    I Y    )  /
           Ũ

$\label{eq21} \mbox{\rm false}$

(21)

Type: Boolean

fricas

determinant [[retract((ⅇ.i * ⅇ.j)/Ũ) for j in 1..dim] for i in 1..dim]

$\label{eq22}{\left( \begin{array}{@{}l} \displaystyle -{{5764801}\ {{q_{2}}^{4}}\ {{\overline{q_{2}}}^{8}}}-{{65883 44}\ {{q_{2}}^{5}}\ {{\overline{q_{2}}}^{7}}}- \ \ \displaystyle {{3294172}\ {{q_{2}}^{6}}\ {{\overline{q_{2}}}^{6}}}-{{941192}\ {{q_{2}}^{7}}\ {{\overline{q_{2}}}^{5}}}-{{168070}\ {{q_{2}}^{8}}\ {{\overline{q_{2}}}^{4}}}- \ \ \displaystyle {{19208}\ {{q_{2}}^{9}}\ {{\overline{q_{2}}}^{3}}}-{{1372}\ {{q_{2}}^{10}}\ {{\overline{q_{2}}}^{2}}}-{{56}\ {{q_{2}}^{11}}\ {\overline{q_{2}}}}-{{q_{2}}^{12}}$

(22)

Type: Expression(Integer)

General Solution

We may consider the problem where multiplication Y is given, and look for all associative scalar products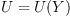

This problem can be solved using linear algebra.

fricas

)expose MCALCFN

   MultiVariableCalculusFunctions is now explicitly exposed in frame 
      initial 
J := jacobian(ravel ω,concat map(variables,ravel U)::List Symbol);

Type: Matrix(Expression(Integer))

fricas

u := transpose matrix [concat map(variables,ravel U)::List Symbol];

Type: Matrix(Polynomial(Integer))

fricas

J::OutputForm * u::OutputForm = 0

$\label{eq23}$

(23)

Type: Equation(OutputForm?)

fricas

nrows(J),ncols(J)

$\label{eq24}\left[{512}, \:{64}\right]$

(24)

Type: Tuple(PositiveInteger?)

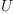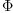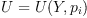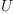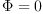The matrix J transforms the coefficients of the tensor into coefficients of the tensor $\Phi$ . We are looking for the general linear family of tensors such that J transforms into $\Phi=0$ for any such .

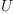If the null space of the J matrix is not empty we can use the basis to find all non-trivial solutions for U:

fricas

Ñ:=nullSpace(J);

Type: List(Vector(Expression(Integer)))

fricas

ℰ:=map((x,y)+->x=y, concat
       map(variables,ravel U), entries Σ(sb('p,[i])*Ñ.i, i,1..#Ñ) )

   >> Error detected within library code:
   reducing over an empty list needs the 3 argument form

This defines a family of Frobenius algebras:

fricas

zero? eval(ω,ℰ)

   There are 12 exposed and 6 unexposed library operations named eval 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op eval
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named eval 
      with argument type(s) 
ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))
                                 Variable(ℰ)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

The pairing is necessarily diagonal!

fricas

Ų:ℒ := eval(U,ℰ)

   There are 12 exposed and 6 unexposed library operations named eval 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op eval
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named eval 
      with argument type(s) 
ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))
                                 Variable(ℰ)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

The scalar product must be non-degenerate:

fricas

Ů:=determinant [[retract((ⅇ.i * ⅇ.j)/Ų) for j in 1..dim] for i in 1..dim]

                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +

   >> Error detected within library code:
   failed

Definition 3

Co-pairing

Solve the Snake Relation as a system of linear equations.

fricas

Um:=matrix [[(ⅇ.i*ⅇ.j)/Ų for i in 1..dim] for j in 1..dim]

                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +
                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +

$\label{eq25}\left[ \begin{array}{cccccccc} {�� \ {|_{\ 0 \ 0}}}&{�� \ {|_{\ 1 \ 0}}}&{�� \ {|_{\ 2 \ 0}}}&{�� \ {|_{\ 3 \ 0}}}&{�� \ {|_{\ 4 \ 0}}}&{�� \ {|_{\ 5 \ 0}}}&{�� \ {|_{\ 6 \ 0}}}&{�� \ {|_{\ 7 \ 0}}} \ {�� \ {|_{\ 0 \ 1}}}&{�� \ {|_{\ 1 \ 1}}}&{�� \ {|_{\ 2 \ 1}}}&{�� \ {|_{\ 3 \ 1}}}&{�� \ {|_{\ 4 \ 1}}}&{�� \ {|_{\ 5 \ 1}}}&{�� \ {|_{\ 6 \ 1}}}&{�� \ {|_{\ 7 \ 1}}} \ {�� \ {|_{\ 0 \ 2}}}&{�� \ {|_{\ 1 \ 2}}}&{�� \ {|_{\ 2 \ 2}}}&{�� \ {|_{\ 3 \ 2}}}&{�� \ {|_{\ 4 \ 2}}}&{�� \ {|_{\ 5 \ 2}}}&{�� \ {|_{\ 6 \ 2}}}&{�� \ {|_{\ 7 \ 2}}} \ {�� \ {|_{\ 0 \ 3}}}&{�� \ {|_{\ 1 \ 3}}}&{�� \ {|_{\ 2 \ 3}}}&{�� \ {|_{\ 3 \ 3}}}&{�� \ {|_{\ 4 \ 3}}}&{�� \ {|_{\ 5 \ 3}}}&{�� \ {|_{\ 6 \ 3}}}&{�� \ {|_{\ 7 \ 3}}} \ {�� \ {|_{\ 0 \ 4}}}&{�� \ {|_{\ 1 \ 4}}}&{�� \ {|_{\ 2 \ 4}}}&{�� \ {|_{\ 3 \ 4}}}&{�� \ {|_{\ 4 \ 4}}}&{�� \ {|_{\ 5 \ 4}}}&{�� \ {|_{\ 6 \ 4}}}&{�� \ {|_{\ 7 \ 4}}} \ {�� \ {|_{\ 0 \ 5}}}&{�� \ {|_{\ 1 \ 5}}}&{�� \ {|_{\ 2 \ 5}}}&{�� \ {|_{\ 3 \ 5}}}&{�� \ {|_{\ 4 \ 5}}}&{�� \ {|_{\ 5 \ 5}}}&{�� \ {|_{\ 6 \ 5}}}&{�� \ {|_{\ 7 \ 5}}} \ {�� \ {|_{\ 0 \ 6}}}&{�� \ {|_{\ 1 \ 6}}}&{�� \ {|_{\ 2 \ 6}}}&{�� \ {|_{\ 3 \ 6}}}&{�� \ {|_{\ 4 \ 6}}}&{�� \ {|_{\ 5 \ 6}}}&{�� \ {|_{\ 6 \ 6}}}&{�� \ {|_{\ 7 \ 6}}} \ {�� \ {|_{\ 0 \ 7}}}&{�� \ {|_{\ 1 \ 7}}}&{�� \ {|_{\ 2 \ 7}}}&{�� \ {|_{\ 3 \ 7}}}&{�� \ {|_{\ 4 \ 7}}}&{�� \ {|_{\ 5 \ 7}}}&{�� \ {|_{\ 6 \ 7}}}&{�� \ {|_{\ 7 \ 7}}}$

(25)

Type: Matrix(ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer)))

fricas

mU:=transpose inverse map(retract,Um)

   >> Error detected within library code:
   failed

Check "dimension" and the snake relations.

fricas

d:ℒ:=
       Ω    /
       X    /
       Ų

                     2
                  0 +
                  - --
                  0  2
                    +
   arity warning: ----
                     2
                  0 +
                  - --
                  0  2
                    +
                   2
                  +  0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +

$\label{eq26}\begin{array}{@{}l} \displaystyle {�� \ �� \ {|_{\ 0 \ 0}^{\ 0 \ 0}}}+{�� \ �� \ {|_{\ 1 \ 0}^{\ 0 \ 1}}}+{�� \ �� \ {|_{\ 2 \ 0}^{\ 0 \ 2}}}+{�� \ �� \ {|_{\ 3 \ 0}^{\ 0 \ 3}}}+{�� \ �� \ {|_{\ 4 \ 0}^{\ 0 \ 4}}}+ \ \ \displaystyle {�� \ �� \ {|_{\ 5 \ 0}^{\ 0 \ 5}}}+{�� \ �� \ {|_{\ 6 \ 0}^{\ 0 \ 6}}}+{�� \ �� \ {|_{\ 7 \ 0}^{\ 0 \ 7}}}+{�� \ �� \ {|_{\ 0 \ 1}^{\ 1 \ 0}}}+{�� \ �� \ {|_{\ 1 \ 1}^{\ 1 \ 1}}}+ \ \ \displaystyle {�� \ �� \ {|_{\ 2 \ 1}^{\ 1 \ 2}}}+{�� \ �� \ {|_{\ 3 \ 1}^{\ 1 \ 3}}}+{�� \ �� \ {|_{\ 4 \ 1}^{\ 1 \ 4}}}+{�� \ �� \ {|_{\ 5 \ 1}^{\ 1 \ 5}}}+{�� \ �� \ {|_{\ 6 \ 1}^{\ 1 \ 6}}}+ \ \ \displaystyle {�� \ �� \ {|_{\ 7 \ 1}^{\ 1 \ 7}}}+{�� \ �� \ {|_{\ 0 \ 2}^{\ 2 \ 0}}}+{�� \ �� \ {|_{\ 1 \ 2}^{\ 2 \ 1}}}+{�� \ �� \ {|_{\ 2 \ 2}^{\ 2 \ 2}}}+{�� \ �� \ {|_{\ 3 \ 2}^{\ 2 \ 3}}}+ \ \ \displaystyle {�� \ �� \ {|_{\ 4 \ 2}^{\ 2 \ 4}}}+{�� \ �� \ {|_{\ 5 \ 2}^{\ 2 \ 5}}}+{�� \ �� \ {|_{\ 6 \ 2}^{\ 2 \ 6}}}+{�� \ �� \ {|_{\ 7 \ 2}^{\ 2 \ 7}}}+{�� \ �� \ {|_{\ 0 \ 3}^{\ 3 \ 0}}}+ \ \ \displaystyle {�� \ �� \ {|_{\ 1 \ 3}^{\ 3 \ 1}}}+{�� \ �� \ {|_{\ 2 \ 3}^{\ 3 \ 2}}}+{�� \ �� \ {|_{\ 3 \ 3}^{\ 3 \ 3}}}+{�� \ �� \ {|_{\ 4 \ 3}^{\ 3 \ 4}}}+{�� \ �� \ {|_{\ 5 \ 3}^{\ 3 \ 5}}}+ \ \ \displaystyle {�� \ �� \ {|_{\ 6 \ 3}^{\ 3 \ 6}}}+{�� \ �� \ {|_{\ 7 \ 3}^{\ 3 \ 7}}}+{�� \ �� \ {|_{\ 0 \ 4}^{\ 4 \ 0}}}+{�� \ �� \ {|_{\ 1 \ 4}^{\ 4 \ 1}}}+{�� \ �� \ {|_{\ 2 \ 4}^{\ 4 \ 2}}}+ \ \ \displaystyle {�� \ �� \ {|_{\ 3 \ 4}^{\ 4 \ 3}}}+{�� \ �� \ {|_{\ 4 \ 4}^{\ 4 \ 4}}}+{�� \ �� \ {|_{\ 5 \ 4}^{\ 4 \ 5}}}+{�� \ �� \ {|_{\ 6 \ 4}^{\ 4 \ 6}}}+{�� \ �� \ {|_{\ 7 \ 4}^{\ 4 \ 7}}}+ \ \ \displaystyle {�� \ �� \ {|_{\ 0 \ 5}^{\ 5 \ 0}}}+{�� \ �� \ {|_{\ 1 \ 5}^{\ 5 \ 1}}}+{�� \ �� \ {|_{\ 2 \ 5}^{\ 5 \ 2}}}+{�� \ �� \ {|_{\ 3 \ 5}^{\ 5 \ 3}}}+{�� \ �� \ {|_{\ 4 \ 5}^{\ 5 \ 4}}}+ \ \ \displaystyle {�� \ �� \ {|_{\ 5 \ 5}^{\ 5 \ 5}}}+{�� \ �� \ {|_{\ 6 \ 5}^{\ 5 \ 6}}}+{�� \ �� \ {|_{\ 7 \ 5}^{\ 5 \ 7}}}+{�� \ �� \ {|_{\ 0 \ 6}^{\ 6 \ 0}}}+{�� \ �� \ {|_{\ 1 \ 6}^{\ 6 \ 1}}}+ \ \ \displaystyle {�� \ �� \ {|_{\ 2 \ 6}^{\ 6 \ 2}}}+{�� \ �� \ {|_{\ 3 \ 6}^{\ 6 \ 3}}}+{�� \ �� \ {|_{\ 4 \ 6}^{\ 6 \ 4}}}+{�� \ �� \ {|_{\ 5 \ 6}^{\ 6 \ 5}}}+{�� \ �� \ {|_{\ 6 \ 6}^{\ 6 \ 6}}}+ \ \ \displaystyle {�� \ �� \ {|_{\ 7 \ 6}^{\ 6 \ 7}}}+{�� \ �� \ {|_{\ 0 \ 7}^{\ 7 \ 0}}}+{�� \ �� \ {|_{\ 1 \ 7}^{\ 7 \ 1}}}+{�� \ �� \ {|_{\ 2 \ 7}^{\ 7 \ 2}}}+{�� \ �� \ {|_{\ 3 \ 7}^{\ 7 \ 3}}}+ \ \ \displaystyle {�� \ �� \ {|_{\ 4 \ 7}^{\ 7 \ 4}}}+{�� \ �� \ {|_{\ 5 \ 7}^{\ 7 \ 5}}}+{�� \ �� \ {|_{\ 6 \ 7}^{\ 7 \ 6}}}+{�� \ �� \ {|_{\ 7 \ 7}^{\ 7 \ 7}}}$

(26)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

test
    (    I Ω     )  /
    (     Ų I    )  =  I

$\label{eq27} \mbox{\rm false}$

(27)

Type: Boolean

fricas

test
    (     Ω I    )  /
    (    I Ų     )  =  I

   There are no library operations named Ω 
      Use HyperDoc Browse or issue
                                 )what op Ω
      to learn if there is any operation containing " Ω " in its name.

   Cannot find a definition or applicable library operation named Ω 
      with argument type(s) 
ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Definition 4

Co-algebra

Compute the "three-point" function and use it to define co-multiplication.

fricas

W:=(Y,I)/Ų

                   3
                  +  0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +

\label{eq28}\begin{array}{@{}l}
\displaystyle
{�� \ {|_{\ 0 \ 0}^{\ 0 \ 0 \ 0}}}+{�� \ {|_{\ 0 \ 1}^{\ 0 \ 0 \ 1}}}+{�� \ {|_{\ 0 \ 2}^{\ 0 \ 0 \ 2}}}+{�� \ {|_{\ 0 \ 3}^{\ 0 \ 0 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 0 \ 4}^{\ 0 \ 0 \ 4}}}+{�� \ {|_{\ 0 \ 5}^{\ 0 \ 0 \ 5}}}+{�� \ {|_{\ 0 \ 6}^{\ 0 \ 0 \ 6}}}+{�� \ {|_{\ 0 \ 7}^{\ 0 \ 0 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 1 \ 0}^{\ 0 \ 1 \ 0}}}+{�� \ {|_{\ 1 \ 1}^{\ 0 \ 1 \ 1}}}+{�� \ {|_{\ 1 \ 2}^{\ 0 \ 1 \ 2}}}+{�� \ {|_{\ 1 \ 3}^{\ 0 \ 1 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 1 \ 4}^{\ 0 \ 1 \ 4}}}+{�� \ {|_{\ 1 \ 5}^{\ 0 \ 1 \ 5}}}+{�� \ {|_{\ 1 \ 6}^{\ 0 \ 1 \ 6}}}+{�� \ {|_{\ 1 \ 7}^{\ 0 \ 1 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 2 \ 0}^{\ 0 \ 2 \ 0}}}+{�� \ {|_{\ 2 \ 1}^{\ 0 \ 2 \ 1}}}+{�� \ {|_{\ 2 \ 2}^{\ 0 \ 2 \ 2}}}+{�� \ {|_{\ 2 \ 3}^{\ 0 \ 2 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 2 \ 4}^{\ 0 \ 2 \ 4}}}+{�� \ {|_{\ 2 \ 5}^{\ 0 \ 2 \ 5}}}+{�� \ {|_{\ 2 \ 6}^{\ 0 \ 2 \ 6}}}+{�� \ {|_{\ 2 \ 7}^{\ 0 \ 2 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 3 \ 0}^{\ 0 \ 3 \ 0}}}+{�� \ {|_{\ 3 \ 1}^{\ 0 \ 3 \ 1}}}+{�� \ {|_{\ 3 \ 2}^{\ 0 \ 3 \ 2}}}+{�� \ {|_{\ 3 \ 3}^{\ 0 \ 3 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 3 \ 4}^{\ 0 \ 3 \ 4}}}+{�� \ {|_{\ 3 \ 5}^{\ 0 \ 3 \ 5}}}+{�� \ {|_{\ 3 \ 6}^{\ 0 \ 3 \ 6}}}+{�� \ {|_{\ 3 \ 7}^{\ 0 \ 3 \ 7}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 0}^{\ 0 \ 4 \ 0}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 1}^{\ 0 \ 4 \ 1}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 2}^{\ 0 \ 4 \ 2}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 3}^{\ 0 \ 4 \ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 0 \ 4 \ 4}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 5}^{\ 0 \ 4 \ 5}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 6}^{\ 0 \ 4 \ 6}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 7}^{\ 0 \ 4 \ 7}}}+{�� \ {|_{\ 5 \ 0}^{\ 0 \ 5 \ 0}}}+{�� \ {|_{\ 5 \ 1}^{\ 0 \ 5 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 2}^{\ 0 \ 5 \ 2}}}+{�� \ {|_{\ 5 \ 3}^{\ 0 \ 5 \ 3}}}+{�� \ {|_{\ 5 \ 4}^{\ 0 \ 5 \ 4}}}+{�� \ {|_{\ 5 \ 5}^{\ 0 \ 5 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 6}^{\ 0 \ 5 \ 6}}}+{�� \ {|_{\ 5 \ 7}^{\ 0 \ 5 \ 7}}}+{�� \ {|_{\ 6 \ 0}^{\ 0 \ 6 \ 0}}}+{�� \ {|_{\ 6 \ 1}^{\ 0 \ 6 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 2}^{\ 0 \ 6 \ 2}}}+{�� \ {|_{\ 6 \ 3}^{\ 0 \ 6 \ 3}}}+{�� \ {|_{\ 6 \ 4}^{\ 0 \ 6 \ 4}}}+{�� \ {|_{\ 6 \ 5}^{\ 0 \ 6 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 6}^{\ 0 \ 6 \ 6}}}+{�� \ {|_{\ 6 \ 7}^{\ 0 \ 6 \ 7}}}+{�� \ {|_{\ 7 \ 0}^{\ 0 \ 7 \ 0}}}+{�� \ {|_{\ 7 \ 1}^{\ 0 \ 7 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 2}^{\ 0 \ 7 \ 2}}}+{�� \ {|_{\ 7 \ 3}^{\ 0 \ 7 \ 3}}}+{�� \ {|_{\ 7 \ 4}^{\ 0 \ 7 \ 4}}}+{�� \ {|_{\ 7 \ 5}^{\ 0 \ 7 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 6}^{\ 0 \ 7 \ 6}}}+{�� \ {|_{\ 7 \ 7}^{\ 0 \ 7 \ 7}}}+{�� \ {|_{\ 1 \ 0}^{\ 1 \ 0 \ 0}}}+{�� \ {|_{\ 1 \ 1}^{\ 1 \ 0 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 1 \ 2}^{\ 1 \ 0 \ 2}}}+{�� \ {|_{\ 1 \ 3}^{\ 1 \ 0 \ 3}}}+{�� \ {|_{\ 1 \ 4}^{\ 1 \ 0 \ 4}}}+{�� \ {|_{\ 1 \ 5}^{\ 1 \ 0 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 1 \ 6}^{\ 1 \ 0 \ 6}}}+{�� \ {|_{\ 1 \ 7}^{\ 1 \ 0 \ 7}}}-{�� \ {|_{\ 0 \ 0}^{\ 1 \ 1 \ 0}}}-{�� \ {|_{\ 0 \ 1}^{\ 1 \ 1 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 0 \ 2}^{\ 1 \ 1 \ 2}}}-{�� \ {|_{\ 0 \ 3}^{\ 1 \ 1 \ 3}}}-{�� \ {|_{\ 0 \ 4}^{\ 1 \ 1 \ 4}}}-{�� \ {|_{\ 0 \ 5}^{\ 1 \ 1 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 0 \ 6}^{\ 1 \ 1 \ 6}}}-{�� \ {|_{\ 0 \ 7}^{\ 1 \ 1 \ 7}}}+{�� \ {|_{\ 3 \ 0}^{\ 1 \ 2 \ 0}}}+{�� \ {|_{\ 3 \ 1}^{\ 1 \ 2 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 3 \ 2}^{\ 1 \ 2 \ 2}}}+{�� \ {|_{\ 3 \ 3}^{\ 1 \ 2 \ 3}}}+{�� \ {|_{\ 3 \ 4}^{\ 1 \ 2 \ 4}}}+{�� \ {|_{\ 3 \ 5}^{\ 1 \ 2 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 3 \ 6}^{\ 1 \ 2 \ 6}}}+{�� \ {|_{\ 3 \ 7}^{\ 1 \ 2 \ 7}}}-{�� \ {|_{\ 2 \ 0}^{\ 1 \ 3 \ 0}}}-{�� \ {|_{\ 2 \ 1}^{\ 1 \ 3 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 2 \ 2}^{\ 1 \ 3 \ 2}}}-{�� \ {|_{\ 2 \ 3}^{\ 1 \ 3 \ 3}}}-{�� \ {|_{\ 2 \ 4}^{\ 1 \ 3 \ 4}}}-{�� \ {|_{\ 2 \ 5}^{\ 1 \ 3 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 2 \ 6}^{\ 1 \ 3 \ 6}}}-{�� \ {|_{\ 2 \ 7}^{\ 1 \ 3 \ 7}}}+{�� \ {|_{\ 5 \ 0}^{\ 1 \ 4 \ 0}}}+{�� \ {|_{\ 5 \ 1}^{\ 1 \ 4 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 2}^{\ 1 \ 4 \ 2}}}+{�� \ {|_{\ 5 \ 3}^{\ 1 \ 4 \ 3}}}+{�� \ {|_{\ 5 \ 4}^{\ 1 \ 4 \ 4}}}+{�� \ {|_{\ 5 \ 5}^{\ 1 \ 4 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 6}^{\ 1 \ 4 \ 6}}}+{�� \ {|_{\ 5 \ 7}^{\ 1 \ 4 \ 7}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 0}^{\ 1 \ 5 \ 0}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 1}^{\ 1 \ 5 \ 1}}}-
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 2}^{\ 1 \ 5 \ 2}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 3}^{\ 1 \ 5 \ 3}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 1 \ 5 \ 4}}}-
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 5}^{\ 1 \ 5 \ 5}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 6}^{\ 1 \ 5 \ 6}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 7}^{\ 1 \ 5 \ 7}}}-
\
\
\displaystyle
{�� \ {|_{\ 7 \ 0}^{\ 1 \ 6 \ 0}}}-{�� \ {|_{\ 7 \ 1}^{\ 1 \ 6 \ 1}}}-{�� \ {|_{\ 7 \ 2}^{\ 1 \ 6 \ 2}}}-{�� \ {|_{\ 7 \ 3}^{\ 1 \ 6 \ 3}}}-
\
\
\displaystyle
{�� \ {|_{\ 7 \ 4}^{\ 1 \ 6 \ 4}}}-{�� \ {|_{\ 7 \ 5}^{\ 1 \ 6 \ 5}}}-{�� \ {|_{\ 7 \ 6}^{\ 1 \ 6 \ 6}}}-{�� \ {|_{\ 7 \ 7}^{\ 1 \ 6 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 0}^{\ 1 \ 7 \ 0}}}+{�� \ {|_{\ 6 \ 1}^{\ 1 \ 7 \ 1}}}+{�� \ {|_{\ 6 \ 2}^{\ 1 \ 7 \ 2}}}+{�� \ {|_{\ 6 \ 3}^{\ 1 \ 7 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 4}^{\ 1 \ 7 \ 4}}}+{�� \ {|_{\ 6 \ 5}^{\ 1 \ 7 \ 5}}}+{�� \ {|_{\ 6 \ 6}^{\ 1 \ 7 \ 6}}}+{�� \ {|_{\ 6 \ 7}^{\ 1 \ 7 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 2 \ 0}^{\ 2 \ 0 \ 0}}}+{�� \ {|_{\ 2 \ 1}^{\ 2 \ 0 \ 1}}}+{�� \ {|_{\ 2 \ 2}^{\ 2 \ 0 \ 2}}}+{�� \ {|_{\ 2 \ 3}^{\ 2 \ 0 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 2 \ 4}^{\ 2 \ 0 \ 4}}}+{�� \ {|_{\ 2 \ 5}^{\ 2 \ 0 \ 5}}}+{�� \ {|_{\ 2 \ 6}^{\ 2 \ 0 \ 6}}}+{�� \ {|_{\ 2 \ 7}^{\ 2 \ 0 \ 7}}}-
\
\
\displaystyle
{�� \ {|_{\ 3 \ 0}^{\ 2 \ 1 \ 0}}}-{�� \ {|_{\ 3 \ 1}^{\ 2 \ 1 \ 1}}}-{�� \ {|_{\ 3 \ 2}^{\ 2 \ 1 \ 2}}}-{�� \ {|_{\ 3 \ 3}^{\ 2 \ 1 \ 3}}}-
\
\
\displaystyle
{�� \ {|_{\ 3 \ 4}^{\ 2 \ 1 \ 4}}}-{�� \ {|_{\ 3 \ 5}^{\ 2 \ 1 \ 5}}}-{�� \ {|_{\ 3 \ 6}^{\ 2 \ 1 \ 6}}}-{�� \ {|_{\ 3 \ 7}^{\ 2 \ 1 \ 7}}}-
\
\
\displaystyle
{�� \ {|_{\ 0 \ 0}^{\ 2 \ 2 \ 0}}}-{�� \ {|_{\ 0 \ 1}^{\ 2 \ 2 \ 1}}}-{�� \ {|_{\ 0 \ 2}^{\ 2 \ 2 \ 2}}}-{�� \ {|_{\ 0 \ 3}^{\ 2 \ 2 \ 3}}}-
\
\
\displaystyle
{�� \ {|_{\ 0 \ 4}^{\ 2 \ 2 \ 4}}}-{�� \ {|_{\ 0 \ 5}^{\ 2 \ 2 \ 5}}}-{�� \ {|_{\ 0 \ 6}^{\ 2 \ 2 \ 6}}}-{�� \ {|_{\ 0 \ 7}^{\ 2 \ 2 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 1 \ 0}^{\ 2 \ 3 \ 0}}}+{�� \ {|_{\ 1 \ 1}^{\ 2 \ 3 \ 1}}}+{�� \ {|_{\ 1 \ 2}^{\ 2 \ 3 \ 2}}}+{�� \ {|_{\ 1 \ 3}^{\ 2 \ 3 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 1 \ 4}^{\ 2 \ 3 \ 4}}}+{�� \ {|_{\ 1 \ 5}^{\ 2 \ 3 \ 5}}}+{�� \ {|_{\ 1 \ 6}^{\ 2 \ 3 \ 6}}}+{�� \ {|_{\ 1 \ 7}^{\ 2 \ 3 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 0}^{\ 2 \ 4 \ 0}}}+{�� \ {|_{\ 6 \ 1}^{\ 2 \ 4 \ 1}}}+{�� \ {|_{\ 6 \ 2}^{\ 2 \ 4 \ 2}}}+{�� \ {|_{\ 6 \ 3}^{\ 2 \ 4 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 4}^{\ 2 \ 4 \ 4}}}+{�� \ {|_{\ 6 \ 5}^{\ 2 \ 4 \ 5}}}+{�� \ {|_{\ 6 \ 6}^{\ 2 \ 4 \ 6}}}+{�� \ {|_{\ 6 \ 7}^{\ 2 \ 4 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 0}^{\ 2 \ 5 \ 0}}}+{�� \ {|_{\ 7 \ 1}^{\ 2 \ 5 \ 1}}}+{�� \ {|_{\ 7 \ 2}^{\ 2 \ 5 \ 2}}}+{�� \ {|_{\ 7 \ 3}^{\ 2 \ 5 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 4}^{\ 2 \ 5 \ 4}}}+{�� \ {|_{\ 7 \ 5}^{\ 2 \ 5 \ 5}}}+{�� \ {|_{\ 7 \ 6}^{\ 2 \ 5 \ 6}}}+{�� \ {|_{\ 7 \ 7}^{\ 2 \ 5 \ 7}}}-
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 0}^{\ 2 \ 6 \ 0}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 1}^{\ 2 \ 6 \ 1}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 2}^{\ 2 \ 6 \ 2}}}-
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 3}^{\ 2 \ 6 \ 3}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 2 \ 6 \ 4}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 5}^{\ 2 \ 6 \ 5}}}-
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 6}^{\ 2 \ 6 \ 6}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 7}^{\ 2 \ 6 \ 7}}}-{�� \ {|_{\ 5 \ 0}^{\ 2 \ 7 \ 0}}}-{�� \ {|_{\ 5 \ 1}^{\ 2 \ 7 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 5 \ 2}^{\ 2 \ 7 \ 2}}}-{�� \ {|_{\ 5 \ 3}^{\ 2 \ 7 \ 3}}}-{�� \ {|_{\ 5 \ 4}^{\ 2 \ 7 \ 4}}}-{�� \ {|_{\ 5 \ 5}^{\ 2 \ 7 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 5 \ 6}^{\ 2 \ 7 \ 6}}}-{�� \ {|_{\ 5 \ 7}^{\ 2 \ 7 \ 7}}}+{�� \ {|_{\ 3 \ 0}^{\ 3 \ 0 \ 0}}}+{�� \ {|_{\ 3 \ 1}^{\ 3 \ 0 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 3 \ 2}^{\ 3 \ 0 \ 2}}}+{�� \ {|_{\ 3 \ 3}^{\ 3 \ 0 \ 3}}}+{�� \ {|_{\ 3 \ 4}^{\ 3 \ 0 \ 4}}}+{�� \ {|_{\ 3 \ 5}^{\ 3 \ 0 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 3 \ 6}^{\ 3 \ 0 \ 6}}}+{�� \ {|_{\ 3 \ 7}^{\ 3 \ 0 \ 7}}}+{�� \ {|_{\ 2 \ 0}^{\ 3 \ 1 \ 0}}}+{�� \ {|_{\ 2 \ 1}^{\ 3 \ 1 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 2 \ 2}^{\ 3 \ 1 \ 2}}}+{�� \ {|_{\ 2 \ 3}^{\ 3 \ 1 \ 3}}}+{�� \ {|_{\ 2 \ 4}^{\ 3 \ 1 \ 4}}}+{�� \ {|_{\ 2 \ 5}^{\ 3 \ 1 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 2 \ 6}^{\ 3 \ 1 \ 6}}}+{�� \ {|_{\ 2 \ 7}^{\ 3 \ 1 \ 7}}}-{�� \ {|_{\ 1 \ 0}^{\ 3 \ 2 \ 0}}}-{�� \ {|_{\ 1 \ 1}^{\ 3 \ 2 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 1 \ 2}^{\ 3 \ 2 \ 2}}}-{�� \ {|_{\ 1 \ 3}^{\ 3 \ 2 \ 3}}}-{�� \ {|_{\ 1 \ 4}^{\ 3 \ 2 \ 4}}}-{�� \ {|_{\ 1 \ 5}^{\ 3 \ 2 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 1 \ 6}^{\ 3 \ 2 \ 6}}}-{�� \ {|_{\ 1 \ 7}^{\ 3 \ 2 \ 7}}}-{�� \ {|_{\ 0 \ 0}^{\ 3 \ 3 \ 0}}}-{�� \ {|_{\ 0 \ 1}^{\ 3 \ 3 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 0 \ 2}^{\ 3 \ 3 \ 2}}}-{�� \ {|_{\ 0 \ 3}^{\ 3 \ 3 \ 3}}}-{�� \ {|_{\ 0 \ 4}^{\ 3 \ 3 \ 4}}}-{�� \ {|_{\ 0 \ 5}^{\ 3 \ 3 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 0 \ 6}^{\ 3 \ 3 \ 6}}}-{�� \ {|_{\ 0 \ 7}^{\ 3 \ 3 \ 7}}}+{�� \ {|_{\ 7 \ 0}^{\ 3 \ 4 \ 0}}}+{�� \ {|_{\ 7 \ 1}^{\ 3 \ 4 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 2}^{\ 3 \ 4 \ 2}}}+{�� \ {|_{\ 7 \ 3}^{\ 3 \ 4 \ 3}}}+{�� \ {|_{\ 7 \ 4}^{\ 3 \ 4 \ 4}}}+{�� \ {|_{\ 7 \ 5}^{\ 3 \ 4 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 6}^{\ 3 \ 4 \ 6}}}+{�� \ {|_{\ 7 \ 7}^{\ 3 \ 4 \ 7}}}-{�� \ {|_{\ 6 \ 0}^{\ 3 \ 5 \ 0}}}-{�� \ {|_{\ 6 \ 1}^{\ 3 \ 5 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 6 \ 2}^{\ 3 \ 5 \ 2}}}-{�� \ {|_{\ 6 \ 3}^{\ 3 \ 5 \ 3}}}-{�� \ {|_{\ 6 \ 4}^{\ 3 \ 5 \ 4}}}-{�� \ {|_{\ 6 \ 5}^{\ 3 \ 5 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 6 \ 6}^{\ 3 \ 5 \ 6}}}-{�� \ {|_{\ 6 \ 7}^{\ 3 \ 5 \ 7}}}+{�� \ {|_{\ 5 \ 0}^{\ 3 \ 6 \ 0}}}+{�� \ {|_{\ 5 \ 1}^{\ 3 \ 6 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 2}^{\ 3 \ 6 \ 2}}}+{�� \ {|_{\ 5 \ 3}^{\ 3 \ 6 \ 3}}}+{�� \ {|_{\ 5 \ 4}^{\ 3 \ 6 \ 4}}}+{�� \ {|_{\ 5 \ 5}^{\ 3 \ 6 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 6}^{\ 3 \ 6 \ 6}}}+{�� \ {|_{\ 5 \ 7}^{\ 3 \ 6 \ 7}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 0}^{\ 3 \ 7 \ 0}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 1}^{\ 3 \ 7 \ 1}}}-
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 2}^{\ 3 \ 7 \ 2}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 3}^{\ 3 \ 7 \ 3}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 3 \ 7 \ 4}}}-
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 5}^{\ 3 \ 7 \ 5}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 6}^{\ 3 \ 7 \ 6}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 7}^{\ 3 \ 7 \ 7}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 0}^{\ 4 \ 0 \ 0}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 1}^{\ 4 \ 0 \ 1}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 2}^{\ 4 \ 0 \ 2}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 3}^{\ 4 \ 0 \ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 4 \ 0 \ 4}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 5}^{\ 4 \ 0 \ 5}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 6}^{\ 4 \ 0 \ 6}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 7}^{\ 4 \ 0 \ 7}}}-{�� \ {|_{\ 5 \ 0}^{\ 4 \ 1 \ 0}}}-{�� \ {|_{\ 5 \ 1}^{\ 4 \ 1 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 5 \ 2}^{\ 4 \ 1 \ 2}}}-{�� \ {|_{\ 5 \ 3}^{\ 4 \ 1 \ 3}}}-{�� \ {|_{\ 5 \ 4}^{\ 4 \ 1 \ 4}}}-{�� \ {|_{\ 5 \ 5}^{\ 4 \ 1 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 5 \ 6}^{\ 4 \ 1 \ 6}}}-{�� \ {|_{\ 5 \ 7}^{\ 4 \ 1 \ 7}}}-{�� \ {|_{\ 6 \ 0}^{\ 4 \ 2 \ 0}}}-{�� \ {|_{\ 6 \ 1}^{\ 4 \ 2 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 6 \ 2}^{\ 4 \ 2 \ 2}}}-{�� \ {|_{\ 6 \ 3}^{\ 4 \ 2 \ 3}}}-{�� \ {|_{\ 6 \ 4}^{\ 4 \ 2 \ 4}}}-{�� \ {|_{\ 6 \ 5}^{\ 4 \ 2 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 6 \ 6}^{\ 4 \ 2 \ 6}}}-{�� \ {|_{\ 6 \ 7}^{\ 4 \ 2 \ 7}}}-{�� \ {|_{\ 7 \ 0}^{\ 4 \ 3 \ 0}}}-{�� \ {|_{\ 7 \ 1}^{\ 4 \ 3 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 7 \ 2}^{\ 4 \ 3 \ 2}}}-{�� \ {|_{\ 7 \ 3}^{\ 4 \ 3 \ 3}}}-{�� \ {|_{\ 7 \ 4}^{\ 4 \ 3 \ 4}}}-{�� \ {|_{\ 7 \ 5}^{\ 4 \ 3 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 7 \ 6}^{\ 4 \ 3 \ 6}}}-{�� \ {|_{\ 7 \ 7}^{\ 4 \ 3 \ 7}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 0}^{\ 4 \ 4 \ 0}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 1}^{\ 4 \ 4 \ 1}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 2}^{\ 4 \ 4 \ 2}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 3}^{\ 4 \ 4 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 4}^{\ 4 \ 4 \ 4}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 5}^{\ 4 \ 4 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 6}^{\ 4 \ 4 \ 6}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 7}^{\ 4 \ 4 \ 7}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 1 \ 0}^{\ 4 \ 5 \ 0}}}+{{q_{2}}\ �� \ {|_{\ 1 \ 1}^{\ 4 \ 5 \ 1}}}+{{q_{2}}\ �� \ {|_{\ 1 \ 2}^{\ 4 \ 5 \ 2}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 1 \ 3}^{\ 4 \ 5 \ 3}}}+{{q_{2}}\ �� \ {|_{\ 1 \ 4}^{\ 4 \ 5 \ 4}}}+{{q_{2}}\ �� \ {|_{\ 1 \ 5}^{\ 4 \ 5 \ 5}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 1 \ 6}^{\ 4 \ 5 \ 6}}}+{{q_{2}}\ �� \ {|_{\ 1 \ 7}^{\ 4 \ 5 \ 7}}}+{{q_{2}}\ �� \ {|_{\ 2 \ 0}^{\ 4 \ 6 \ 0}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 2 \ 1}^{\ 4 \ 6 \ 1}}}+{{q_{2}}\ �� \ {|_{\ 2 \ 2}^{\ 4 \ 6 \ 2}}}+{{q_{2}}\ �� \ {|_{\ 2 \ 3}^{\ 4 \ 6 \ 3}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 2 \ 4}^{\ 4 \ 6 \ 4}}}+{{q_{2}}\ �� \ {|_{\ 2 \ 5}^{\ 4 \ 6 \ 5}}}+{{q_{2}}\ �� \ {|_{\ 2 \ 6}^{\ 4 \ 6 \ 6}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 2 \ 7}^{\ 4 \ 6 \ 7}}}+{{q_{2}}\ �� \ {|_{\ 3 \ 0}^{\ 4 \ 7 \ 0}}}+{{q_{2}}\ �� \ {|_{\ 3 \ 1}^{\ 4 \ 7 \ 1}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 3 \ 2}^{\ 4 \ 7 \ 2}}}+{{q_{2}}\ �� \ {|_{\ 3 \ 3}^{\ 4 \ 7 \ 3}}}+{{q_{2}}\ �� \ {|_{\ 3 \ 4}^{\ 4 \ 7 \ 4}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 3 \ 5}^{\ 4 \ 7 \ 5}}}+{{q_{2}}\ �� \ {|_{\ 3 \ 6}^{\ 4 \ 7 \ 6}}}+{{q_{2}}\ �� \ {|_{\ 3 \ 7}^{\ 4 \ 7 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 0}^{\ 5 \ 0 \ 0}}}+{�� \ {|_{\ 5 \ 1}^{\ 5 \ 0 \ 1}}}+{�� \ {|_{\ 5 \ 2}^{\ 5 \ 0 \ 2}}}+{�� \ {|_{\ 5 \ 3}^{\ 5 \ 0 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 4}^{\ 5 \ 0 \ 4}}}+{�� \ {|_{\ 5 \ 5}^{\ 5 \ 0 \ 5}}}+{�� \ {|_{\ 5 \ 6}^{\ 5 \ 0 \ 6}}}+{�� \ {|_{\ 5 \ 7}^{\ 5 \ 0 \ 7}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 0}^{\ 5 \ 1 \ 0}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 1}^{\ 5 \ 1 \ 1}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 2}^{\ 5 \ 1 \ 2}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 3}^{\ 5 \ 1 \ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 5 \ 1 \ 4}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 5}^{\ 5 \ 1 \ 5}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 6}^{\ 5 \ 1 \ 6}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 7}^{\ 5 \ 1 \ 7}}}-{�� \ {|_{\ 7 \ 0}^{\ 5 \ 2 \ 0}}}-{�� \ {|_{\ 7 \ 1}^{\ 5 \ 2 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 7 \ 2}^{\ 5 \ 2 \ 2}}}-{�� \ {|_{\ 7 \ 3}^{\ 5 \ 2 \ 3}}}-{�� \ {|_{\ 7 \ 4}^{\ 5 \ 2 \ 4}}}-{�� \ {|_{\ 7 \ 5}^{\ 5 \ 2 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 7 \ 6}^{\ 5 \ 2 \ 6}}}-{�� \ {|_{\ 7 \ 7}^{\ 5 \ 2 \ 7}}}+{�� \ {|_{\ 6 \ 0}^{\ 5 \ 3 \ 0}}}+{�� \ {|_{\ 6 \ 1}^{\ 5 \ 3 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 2}^{\ 5 \ 3 \ 2}}}+{�� \ {|_{\ 6 \ 3}^{\ 5 \ 3 \ 3}}}+{�� \ {|_{\ 6 \ 4}^{\ 5 \ 3 \ 4}}}+{�� \ {|_{\ 6 \ 5}^{\ 5 \ 3 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 6}^{\ 5 \ 3 \ 6}}}+{�� \ {|_{\ 6 \ 7}^{\ 5 \ 3 \ 7}}}-{{q_{2}}\ �� \ {|_{\ 1 \ 0}^{\ 5 \ 4 \ 0}}}-{{q_{2}}\ �� \ {|_{\ 1 \ 1}^{\ 5 \ 4 \ 1}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 1 \ 2}^{\ 5 \ 4 \ 2}}}-{{q_{2}}\ �� \ {|_{\ 1 \ 3}^{\ 5 \ 4 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 1 \ 4}^{\ 5 \ 4 \ 4}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 1 \ 5}^{\ 5 \ 4 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 1 \ 6}^{\ 5 \ 4 \ 6}}}-{{q_{2}}\ �� \ {|_{\ 1 \ 7}^{\ 5 \ 4 \ 7}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 0}^{\ 5 \ 5 \ 0}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 1}^{\ 5 \ 5 \ 1}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 2}^{\ 5 \ 5 \ 2}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 3}^{\ 5 \ 5 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 4}^{\ 5 \ 5 \ 4}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 5}^{\ 5 \ 5 \ 5}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 6}^{\ 5 \ 5 \ 6}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 7}^{\ 5 \ 5 \ 7}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 0}^{\ 5 \ 6 \ 0}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 1}^{\ 5 \ 6 \ 1}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 2}^{\ 5 \ 6 \ 2}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 3}^{\ 5 \ 6 \ 3}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 4}^{\ 5 \ 6 \ 4}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 5}^{\ 5 \ 6 \ 5}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 6}^{\ 5 \ 6 \ 6}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 7}^{\ 5 \ 6 \ 7}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 0}^{\ 5 \ 7 \ 0}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 1}^{\ 5 \ 7 \ 1}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 2}^{\ 5 \ 7 \ 2}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 3}^{\ 5 \ 7 \ 3}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 4}^{\ 5 \ 7 \ 4}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 5}^{\ 5 \ 7 \ 5}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 6}^{\ 5 \ 7 \ 6}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 7}^{\ 5 \ 7 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 0}^{\ 6 \ 0 \ 0}}}+{�� \ {|_{\ 6 \ 1}^{\ 6 \ 0 \ 1}}}+{�� \ {|_{\ 6 \ 2}^{\ 6 \ 0 \ 2}}}+{�� \ {|_{\ 6 \ 3}^{\ 6 \ 0 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 4}^{\ 6 \ 0 \ 4}}}+{�� \ {|_{\ 6 \ 5}^{\ 6 \ 0 \ 5}}}+{�� \ {|_{\ 6 \ 6}^{\ 6 \ 0 \ 6}}}+{�� \ {|_{\ 6 \ 7}^{\ 6 \ 0 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 0}^{\ 6 \ 1 \ 0}}}+{�� \ {|_{\ 7 \ 1}^{\ 6 \ 1 \ 1}}}+{�� \ {|_{\ 7 \ 2}^{\ 6 \ 1 \ 2}}}+{�� \ {|_{\ 7 \ 3}^{\ 6 \ 1 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 4}^{\ 6 \ 1 \ 4}}}+{�� \ {|_{\ 7 \ 5}^{\ 6 \ 1 \ 5}}}+{�� \ {|_{\ 7 \ 6}^{\ 6 \ 1 \ 6}}}+{�� \ {|_{\ 7 \ 7}^{\ 6 \ 1 \ 7}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 0}^{\ 6 \ 2 \ 0}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 1}^{\ 6 \ 2 \ 1}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 2}^{\ 6 \ 2 \ 2}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 3}^{\ 6 \ 2 \ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 6 \ 2 \ 4}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 5}^{\ 6 \ 2 \ 5}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 6}^{\ 6 \ 2 \ 6}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 7}^{\ 6 \ 2 \ 7}}}-{�� \ {|_{\ 5 \ 0}^{\ 6 \ 3 \ 0}}}-{�� \ {|_{\ 5 \ 1}^{\ 6 \ 3 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 5 \ 2}^{\ 6 \ 3 \ 2}}}-{�� \ {|_{\ 5 \ 3}^{\ 6 \ 3 \ 3}}}-{�� \ {|_{\ 5 \ 4}^{\ 6 \ 3 \ 4}}}-{�� \ {|_{\ 5 \ 5}^{\ 6 \ 3 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 5 \ 6}^{\ 6 \ 3 \ 6}}}-{�� \ {|_{\ 5 \ 7}^{\ 6 \ 3 \ 7}}}-{{q_{2}}\ �� \ {|_{\ 2 \ 0}^{\ 6 \ 4 \ 0}}}-{{q_{2}}\ �� \ {|_{\ 2 \ 1}^{\ 6 \ 4 \ 1}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 2 \ 2}^{\ 6 \ 4 \ 2}}}-{{q_{2}}\ �� \ {|_{\ 2 \ 3}^{\ 6 \ 4 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 2 \ 4}^{\ 6 \ 4 \ 4}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 2 \ 5}^{\ 6 \ 4 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 2 \ 6}^{\ 6 \ 4 \ 6}}}-{{q_{2}}\ �� \ {|_{\ 2 \ 7}^{\ 6 \ 4 \ 7}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 0}^{\ 6 \ 5 \ 0}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 1}^{\ 6 \ 5 \ 1}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 2}^{\ 6 \ 5 \ 2}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 3}^{\ 6 \ 5 \ 3}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 4}^{\ 6 \ 5 \ 4}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 5}^{\ 6 \ 5 \ 5}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 6}^{\ 6 \ 5 \ 6}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 7}^{\ 6 \ 5 \ 7}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 0}^{\ 6 \ 6 \ 0}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 1}^{\ 6 \ 6 \ 1}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 2}^{\ 6 \ 6 \ 2}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 3}^{\ 6 \ 6 \ 3}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 4}^{\ 6 \ 6 \ 4}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 5}^{\ 6 \ 6 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 6}^{\ 6 \ 6 \ 6}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 7}^{\ 6 \ 6 \ 7}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 0}^{\ 6 \ 7 \ 0}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 1}^{\ 6 \ 7 \ 1}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 2}^{\ 6 \ 7 \ 2}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 3}^{\ 6 \ 7 \ 3}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 4}^{\ 6 \ 7 \ 4}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 5}^{\ 6 \ 7 \ 5}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 6}^{\ 6 \ 7 \ 6}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 7}^{\ 6 \ 7 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 0}^{\ 7 \ 0 \ 0}}}+{�� \ {|_{\ 7 \ 1}^{\ 7 \ 0 \ 1}}}+{�� \ {|_{\ 7 \ 2}^{\ 7 \ 0 \ 2}}}+{�� \ {|_{\ 7 \ 3}^{\ 7 \ 0 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 4}^{\ 7 \ 0 \ 4}}}+{�� \ {|_{\ 7 \ 5}^{\ 7 \ 0 \ 5}}}+{�� \ {|_{\ 7 \ 6}^{\ 7 \ 0 \ 6}}}+{�� \ {|_{\ 7 \ 7}^{\ 7 \ 0 \ 7}}}-
\
\
\displaystyle
{�� \ {|_{\ 6 \ 0}^{\ 7 \ 1 \ 0}}}-{�� \ {|_{\ 6 \ 1}^{\ 7 \ 1 \ 1}}}-{�� \ {|_{\ 6 \ 2}^{\ 7 \ 1 \ 2}}}-{�� \ {|_{\ 6 \ 3}^{\ 7 \ 1 \ 3}}}-
\
\
\displaystyle
{�� \ {|_{\ 6 \ 4}^{\ 7 \ 1 \ 4}}}-{�� \ {|_{\ 6 \ 5}^{\ 7 \ 1 \ 5}}}-{�� \ {|_{\ 6 \ 6}^{\ 7 \ 1 \ 6}}}-{�� \ {|_{\ 6 \ 7}^{\ 7 \ 1 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 0}^{\ 7 \ 2 \ 0}}}+{�� \ {|_{\ 5 \ 1}^{\ 7 \ 2 \ 1}}}+{�� \ {|_{\ 5 \ 2}^{\ 7 \ 2 \ 2}}}+{�� \ {|_{\ 5 \ 3}^{\ 7 \ 2 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 4}^{\ 7 \ 2 \ 4}}}+{�� \ {|_{\ 5 \ 5}^{\ 7 \ 2 \ 5}}}+{�� \ {|_{\ 5 \ 6}^{\ 7 \ 2 \ 6}}}+{�� \ {|_{\ 5 \ 7}^{\ 7 \ 2 \ 7}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 0}^{\ 7 \ 3 \ 0}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 1}^{\ 7 \ 3 \ 1}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 2}^{\ 7 \ 3 \ 2}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 3}^{\ 7 \ 3 \ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 7 \ 3 \ 4}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 5}^{\ 7 \ 3 \ 5}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 6}^{\ 7 \ 3 \ 6}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 7}^{\ 7 \ 3 \ 7}}}-{{q_{2}}\ �� \ {|_{\ 3 \ 0}^{\ 7 \ 4 \ 0}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 3 \ 1}^{\ 7 \ 4 \ 1}}}-{{q_{2}}\ �� \ {|_{\ 3 \ 2}^{\ 7 \ 4 \ 2}}}-{{q_{2}}\ �� \ {|_{\ 3 \ 3}^{\ 7 \ 4 \ 3}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 3 \ 4}^{\ 7 \ 4 \ 4}}}-{{q_{2}}\ �� \ {|_{\ 3 \ 5}^{\ 7 \ 4 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 3 \ 6}^{\ 7 \ 4 \ 6}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 3 \ 7}^{\ 7 \ 4 \ 7}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 0}^{\ 7 \ 5 \ 0}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 1}^{\ 7 \ 5 \ 1}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 2}^{\ 7 \ 5 \ 2}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 3}^{\ 7 \ 5 \ 3}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 4}^{\ 7 \ 5 \ 4}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 5}^{\ 7 \ 5 \ 5}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 6}^{\ 7 \ 5 \ 6}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 7}^{\ 7 \ 5 \ 7}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 0}^{\ 7 \ 6 \ 0}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 1}^{\ 7 \ 6 \ 1}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 2}^{\ 7 \ 6 \ 2}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 3}^{\ 7 \ 6 \ 3}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 4}^{\ 7 \ 6 \ 4}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 5}^{\ 7 \ 6 \ 5}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 6}^{\ 7 \ 6 \ 6}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 7}^{\ 7 \ 6 \ 7}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 0}^{\ 7 \ 7 \ 0}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 1}^{\ 7 \ 7 \ 1}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 2}^{\ 7 \ 7 \ 2}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 3}^{\ 7 \ 7 \ 3}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 4}^{\ 7 \ 7 \ 4}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 5}^{\ 7 \ 7 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 6}^{\ 7 \ 7 \ 6}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 7}^{\ 7 \ 7 \ 7}}}

(28)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

λ:=(Ω,I,Ω)/(I,W,I)

                     4
                  + +
                  - --
                  +  4
                    +
   arity warning: ----
                     5
                  0 +
                  - --
                  0  4
                    +

   >> System error:
   Heap exhausted (no more space for allocation).
There are still 807796736 bytes available; the request was for 1073741840 bytes.

PROCEED WITH CAUTION.

fricas

test
     (    I Ω     )  /
     (     Y I    )  =  λ

                     2
                  + +
                  - --
                  +  2
                    +
   arity warning: ----
                     3
                  0 +
                  - --
                  0  2
                    +

$\label{eq29} \mbox{\rm false}$

(29)

Type: Boolean

fricas

test
     (     Ω I    )  /
     (    I Y     )  =  λ

   There are no library operations named Ω 
      Use HyperDoc Browse or issue
                                 )what op Ω
      to learn if there is any operation containing " Ω " in its name.

   Cannot find a definition or applicable library operation named Ω 
      with argument type(s) 
ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Frobenius Condition

Octonion algebra fails the Frobenius Condition!

fricas

H :=
       Y    /
       λ

                   2
                  +  0
                  -- -
                   + 0
   arity warning: ----
                   + 0
                   - -
                   + 0

$\label{eq30}\begin{array}{@{}l} \displaystyle {�� \ {|_{\ 0}^{\ 0 \ 0}}}+{�� \ {|_{\ 1}^{\ 0 \ 1}}}+{�� \ {|_{\ 2}^{\ 0 \ 2}}}+{�� \ {|_{\ 3}^{\ 0 \ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 0 \ 4}}}+ \ \ \displaystyle {�� \ {|_{\ 5}^{\ 0 \ 5}}}+{�� \ {|_{\ 6}^{\ 0 \ 6}}}+{�� \ {|_{\ 7}^{\ 0 \ 7}}}+{�� \ {|_{\ 1}^{\ 1 \ 0}}}-{�� \ {|_{\ 0}^{\ 1 \ 1}}}+{�� \ {|_{\ 3}^{\ 1 \ 2}}}- \ \ \displaystyle {�� \ {|_{\ 2}^{\ 1 \ 3}}}+{�� \ {|_{\ 5}^{\ 1 \ 4}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 1 \ 5}}}-{�� \ {|_{\ 7}^{\ 1 \ 6}}}+{�� \ {|_{\ 6}^{\ 1 \ 7}}}+ \ \ \displaystyle {�� \ {|_{\ 2}^{\ 2 \ 0}}}-{�� \ {|_{\ 3}^{\ 2 \ 1}}}-{�� \ {|_{\ 0}^{\ 2 \ 2}}}+{�� \ {|_{\ 1}^{\ 2 \ 3}}}+{�� \ {|_{\ 6}^{\ 2 \ 4}}}+{�� \ {|_{\ 7}^{\ 2 \ 5}}}- \ \ \displaystyle {{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 2 \ 6}}}-{�� \ {|_{\ 5}^{\ 2 \ 7}}}+{�� \ {|_{\ 3}^{\ 3 \ 0}}}+{�� \ {|_{\ 2}^{\ 3 \ 1}}}-{�� \ {|_{\ 1}^{\ 3 \ 2}}}- \ \ \displaystyle {�� \ {|_{\ 0}^{\ 3 \ 3}}}+{�� \ {|_{\ 7}^{\ 3 \ 4}}}-{�� \ {|_{\ 6}^{\ 3 \ 5}}}+{�� \ {|_{\ 5}^{\ 3 \ 6}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 3 \ 7}}}+ \ \ \displaystyle {{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 4 \ 0}}}-{�� \ {|_{\ 5}^{\ 4 \ 1}}}-{�� \ {|_{\ 6}^{\ 4 \ 2}}}-{�� \ {|_{\ 7}^{\ 4 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 0}^{\ 4 \ 4}}}+ \ \ \displaystyle {{q_{2}}\ �� \ {|_{\ 1}^{\ 4 \ 5}}}+{{q_{2}}\ �� \ {|_{\ 2}^{\ 4 \ 6}}}+{{q_{2}}\ �� \ {|_{\ 3}^{\ 4 \ 7}}}+{�� \ {|_{\ 5}^{\ 5 \ 0}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 5 \ 1}}}- \ \ \displaystyle {�� \ {|_{\ 7}^{\ 5 \ 2}}}+{�� \ {|_{\ 6}^{\ 5 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 1}^{\ 5 \ 4}}}-{{q_{2}}\ �� \ {|_{\ 0}^{\ 5 \ 5}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 3}^{\ 5 \ 6}}}+ \ \ \displaystyle {�� \ {\overline{q_{2}}}\ {|_{\ 2}^{\ 5 \ 7}}}+{�� \ {|_{\ 6}^{\ 6 \ 0}}}+{�� \ {|_{\ 7}^{\ 6 \ 1}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 6 \ 2}}}-{�� \ {|_{\ 5}^{\ 6 \ 3}}}- \ \ \displaystyle {{q_{2}}\ �� \ {|_{\ 2}^{\ 6 \ 4}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 3}^{\ 6 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 0}^{\ 6 \ 6}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 1}^{\ 6 \ 7}}}+{�� \ {|_{\ 7}^{\ 7 \ 0}}}- \ \ \displaystyle {�� \ {|_{\ 6}^{\ 7 \ 1}}}+{�� \ {|_{\ 5}^{\ 7 \ 2}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 7 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 3}^{\ 7 \ 4}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 2}^{\ 7 \ 5}}}+ \ \ \displaystyle {�� \ {\overline{q_{2}}}\ {|_{\ 1}^{\ 7 \ 6}}}-{{q_{2}}\ �� \ {|_{\ 0}^{\ 7 \ 7}}}$

(30)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

Hr := (λ,I)/(I,Y)

                     2
                  + +
                  - --
                  +  2
                    +
   arity warning: ----
                     3
                  0 +
                  - --
                  0  2
                    +

\label{eq31}\begin{array}{@{}l}
\displaystyle
{�� \ {|_{\ 0 \ 0}^{\ 0 \ 0 \ 0}}}+{�� \ {|_{\ 0 \ 1}^{\ 0 \ 0 \ 1}}}+{�� \ {|_{\ 0 \ 2}^{\ 0 \ 0 \ 2}}}+{�� \ {|_{\ 0 \ 3}^{\ 0 \ 0 \ 3}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 0 \ 4}^{\ 0 \ 0 \ 4}}}+{�� \ {|_{\ 0 \ 5}^{\ 0 \ 0 \ 5}}}+{�� \ {|_{\ 0 \ 6}^{\ 0 \ 0 \ 6}}}+{�� \ {|_{\ 0 \ 7}^{\ 0 \ 0 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 0 \ 1}^{\ 0 \ 1 \ 0}}}-{�� \ {|_{\ 0 \ 0}^{\ 0 \ 1 \ 1}}}+{�� \ {|_{\ 0 \ 3}^{\ 0 \ 1 \ 2}}}-{�� \ {|_{\ 0 \ 2}^{\ 0 \ 1 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 0 \ 5}^{\ 0 \ 1 \ 4}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 0 \ 4}^{\ 0 \ 1 \ 5}}}-{�� \ {|_{\ 0 \ 7}^{\ 0 \ 1 \ 6}}}+{�� \ {|_{\ 0 \ 6}^{\ 0 \ 1 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 0 \ 2}^{\ 0 \ 2 \ 0}}}-{�� \ {|_{\ 0 \ 3}^{\ 0 \ 2 \ 1}}}-{�� \ {|_{\ 0 \ 0}^{\ 0 \ 2 \ 2}}}+{�� \ {|_{\ 0 \ 1}^{\ 0 \ 2 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 0 \ 6}^{\ 0 \ 2 \ 4}}}+{�� \ {|_{\ 0 \ 7}^{\ 0 \ 2 \ 5}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 0 \ 4}^{\ 0 \ 2 \ 6}}}-{�� \ {|_{\ 0 \ 5}^{\ 0 \ 2 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 0 \ 3}^{\ 0 \ 3 \ 0}}}+{�� \ {|_{\ 0 \ 2}^{\ 0 \ 3 \ 1}}}-{�� \ {|_{\ 0 \ 1}^{\ 0 \ 3 \ 2}}}-{�� \ {|_{\ 0 \ 0}^{\ 0 \ 3 \ 3}}}+
\
\
\displaystyle
{�� \ {|_{\ 0 \ 7}^{\ 0 \ 3 \ 4}}}-{�� \ {|_{\ 0 \ 6}^{\ 0 \ 3 \ 5}}}+{�� \ {|_{\ 0 \ 5}^{\ 0 \ 3 \ 6}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 0 \ 4}^{\ 0 \ 3 \ 7}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 0 \ 4}^{\ 0 \ 4 \ 0}}}-{�� \ {|_{\ 0 \ 5}^{\ 0 \ 4 \ 1}}}-{�� \ {|_{\ 0 \ 6}^{\ 0 \ 4 \ 2}}}-{�� \ {|_{\ 0 \ 7}^{\ 0 \ 4 \ 3}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 0}^{\ 0 \ 4 \ 4}}}+{{q_{2}}\ �� \ {|_{\ 0 \ 1}^{\ 0 \ 4 \ 5}}}+{{q_{2}}\ �� \ {|_{\ 0 \ 2}^{\ 0 \ 4 \ 6}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 3}^{\ 0 \ 4 \ 7}}}+{�� \ {|_{\ 0 \ 5}^{\ 0 \ 5 \ 0}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 0 \ 4}^{\ 0 \ 5 \ 1}}}-{�� \ {|_{\ 0 \ 7}^{\ 0 \ 5 \ 2}}}+
\
\
\displaystyle
{�� \ {|_{\ 0 \ 6}^{\ 0 \ 5 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 1}^{\ 0 \ 5 \ 4}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 0}^{\ 0 \ 5 \ 5}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 0 \ 3}^{\ 0 \ 5 \ 6}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 0 \ 2}^{\ 0 \ 5 \ 7}}}+{�� \ {|_{\ 0 \ 6}^{\ 0 \ 6 \ 0}}}+{�� \ {|_{\ 0 \ 7}^{\ 0 \ 6 \ 1}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 0 \ 4}^{\ 0 \ 6 \ 2}}}-{�� \ {|_{\ 0 \ 5}^{\ 0 \ 6 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 2}^{\ 0 \ 6 \ 4}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 0 \ 3}^{\ 0 \ 6 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 0 \ 0}^{\ 0 \ 6 \ 6}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 0 \ 1}^{\ 0 \ 6 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 0 \ 7}^{\ 0 \ 7 \ 0}}}-{�� \ {|_{\ 0 \ 6}^{\ 0 \ 7 \ 1}}}+{�� \ {|_{\ 0 \ 5}^{\ 0 \ 7 \ 2}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 0 \ 4}^{\ 0 \ 7 \ 3}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 3}^{\ 0 \ 7 \ 4}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 0 \ 2}^{\ 0 \ 7 \ 5}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 0 \ 1}^{\ 0 \ 7 \ 6}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 0 \ 0}^{\ 0 \ 7 \ 7}}}+{�� \ {|_{\ 1 \ 0}^{\ 1 \ 0 \ 0}}}+{�� \ {|_{\ 1 \ 1}^{\ 1 \ 0 \ 1}}}+{�� \ {|_{\ 1 \ 2}^{\ 1 \ 0 \ 2}}}+
\
\
\displaystyle
{�� \ {|_{\ 1 \ 3}^{\ 1 \ 0 \ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 1 \ 4}^{\ 1 \ 0 \ 4}}}+{�� \ {|_{\ 1 \ 5}^{\ 1 \ 0 \ 5}}}+{�� \ {|_{\ 1 \ 6}^{\ 1 \ 0 \ 6}}}+
\
\
\displaystyle
{�� \ {|_{\ 1 \ 7}^{\ 1 \ 0 \ 7}}}+{�� \ {|_{\ 1 \ 1}^{\ 1 \ 1 \ 0}}}-{�� \ {|_{\ 1 \ 0}^{\ 1 \ 1 \ 1}}}+{�� \ {|_{\ 1 \ 3}^{\ 1 \ 1 \ 2}}}-
\
\
\displaystyle
{�� \ {|_{\ 1 \ 2}^{\ 1 \ 1 \ 3}}}+{�� \ {|_{\ 1 \ 5}^{\ 1 \ 1 \ 4}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 1 \ 4}^{\ 1 \ 1 \ 5}}}-{�� \ {|_{\ 1 \ 7}^{\ 1 \ 1 \ 6}}}+
\
\
\displaystyle
{�� \ {|_{\ 1 \ 6}^{\ 1 \ 1 \ 7}}}+{�� \ {|_{\ 1 \ 2}^{\ 1 \ 2 \ 0}}}-{�� \ {|_{\ 1 \ 3}^{\ 1 \ 2 \ 1}}}-{�� \ {|_{\ 1 \ 0}^{\ 1 \ 2 \ 2}}}+
\
\
\displaystyle
{�� \ {|_{\ 1 \ 1}^{\ 1 \ 2 \ 3}}}+{�� \ {|_{\ 1 \ 6}^{\ 1 \ 2 \ 4}}}+{�� \ {|_{\ 1 \ 7}^{\ 1 \ 2 \ 5}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 1 \ 4}^{\ 1 \ 2 \ 6}}}-
\
\
\displaystyle
{�� \ {|_{\ 1 \ 5}^{\ 1 \ 2 \ 7}}}+{�� \ {|_{\ 1 \ 3}^{\ 1 \ 3 \ 0}}}+{�� \ {|_{\ 1 \ 2}^{\ 1 \ 3 \ 1}}}-{�� \ {|_{\ 1 \ 1}^{\ 1 \ 3 \ 2}}}-
\
\
\displaystyle
{�� \ {|_{\ 1 \ 0}^{\ 1 \ 3 \ 3}}}+{�� \ {|_{\ 1 \ 7}^{\ 1 \ 3 \ 4}}}-{�� \ {|_{\ 1 \ 6}^{\ 1 \ 3 \ 5}}}+{�� \ {|_{\ 1 \ 5}^{\ 1 \ 3 \ 6}}}-
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 1 \ 4}^{\ 1 \ 3 \ 7}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 1 \ 4}^{\ 1 \ 4 \ 0}}}-{�� \ {|_{\ 1 \ 5}^{\ 1 \ 4 \ 1}}}-{�� \ {|_{\ 1 \ 6}^{\ 1 \ 4 \ 2}}}-
\
\
\displaystyle
{�� \ {|_{\ 1 \ 7}^{\ 1 \ 4 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 1 \ 0}^{\ 1 \ 4 \ 4}}}+{{q_{2}}\ �� \ {|_{\ 1 \ 1}^{\ 1 \ 4 \ 5}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 1 \ 2}^{\ 1 \ 4 \ 6}}}+{{q_{2}}\ �� \ {|_{\ 1 \ 3}^{\ 1 \ 4 \ 7}}}+{�� \ {|_{\ 1 \ 5}^{\ 1 \ 5 \ 0}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 1 \ 4}^{\ 1 \ 5 \ 1}}}-{�� \ {|_{\ 1 \ 7}^{\ 1 \ 5 \ 2}}}+{�� \ {|_{\ 1 \ 6}^{\ 1 \ 5 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 1 \ 1}^{\ 1 \ 5 \ 4}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 1 \ 0}^{\ 1 \ 5 \ 5}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 3}^{\ 1 \ 5 \ 6}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 2}^{\ 1 \ 5 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 1 \ 6}^{\ 1 \ 6 \ 0}}}+{�� \ {|_{\ 1 \ 7}^{\ 1 \ 6 \ 1}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 1 \ 4}^{\ 1 \ 6 \ 2}}}-{�� \ {|_{\ 1 \ 5}^{\ 1 \ 6 \ 3}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 1 \ 2}^{\ 1 \ 6 \ 4}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 3}^{\ 1 \ 6 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 1 \ 0}^{\ 1 \ 6 \ 6}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 1}^{\ 1 \ 6 \ 7}}}+{�� \ {|_{\ 1 \ 7}^{\ 1 \ 7 \ 0}}}-{�� \ {|_{\ 1 \ 6}^{\ 1 \ 7 \ 1}}}+{�� \ {|_{\ 1 \ 5}^{\ 1 \ 7 \ 2}}}+ \
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 1 \ 4}^{\ 1 \ 7 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 1 \ 3}^{\ 1 \ 7 \ 4}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 2}^{\ 1 \ 7 \ 5}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 1 \ 1}^{\ 1 \ 7 \ 6}}}-{{q_{2}}\ �� \ {|_{\ 1 \ 0}^{\ 1 \ 7 \ 7}}}+{�� \ {|_{\ 2 \ 0}^{\ 2 \ 0 \ 0}}}+{�� \ {|_{\ 2 \ 1}^{\ 2 \ 0 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 2 \ 2}^{\ 2 \ 0 \ 2}}}+{�� \ {|_{\ 2 \ 3}^{\ 2 \ 0 \ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 2 \ 4}^{\ 2 \ 0 \ 4}}}+{�� \ {|_{\ 2 \ 5}^{\ 2 \ 0 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 2 \ 6}^{\ 2 \ 0 \ 6}}}+{�� \ {|_{\ 2 \ 7}^{\ 2 \ 0 \ 7}}}+{�� \ {|_{\ 2 \ 1}^{\ 2 \ 1 \ 0}}}-{�� \ {|_{\ 2 \ 0}^{\ 2 \ 1 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 2 \ 3}^{\ 2 \ 1 \ 2}}}-{�� \ {|_{\ 2 \ 2}^{\ 2 \ 1 \ 3}}}+{�� \ {|_{\ 2 \ 5}^{\ 2 \ 1 \ 4}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 2 \ 4}^{\ 2 \ 1 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 2 \ 7}^{\ 2 \ 1 \ 6}}}+{�� \ {|_{\ 2 \ 6}^{\ 2 \ 1 \ 7}}}+{�� \ {|_{\ 2 \ 2}^{\ 2 \ 2 \ 0}}}-{�� \ {|_{\ 2 \ 3}^{\ 2 \ 2 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 2 \ 0}^{\ 2 \ 2 \ 2}}}+{�� \ {|_{\ 2 \ 1}^{\ 2 \ 2 \ 3}}}+{�� \ {|_{\ 2 \ 6}^{\ 2 \ 2 \ 4}}}+{�� \ {|_{\ 2 \ 7}^{\ 2 \ 2 \ 5}}}-
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 2 \ 4}^{\ 2 \ 2 \ 6}}}-{�� \ {|_{\ 2 \ 5}^{\ 2 \ 2 \ 7}}}+{�� \ {|_{\ 2 \ 3}^{\ 2 \ 3 \ 0}}}+{�� \ {|_{\ 2 \ 2}^{\ 2 \ 3 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 2 \ 1}^{\ 2 \ 3 \ 2}}}-{�� \ {|_{\ 2 \ 0}^{\ 2 \ 3 \ 3}}}+{�� \ {|_{\ 2 \ 7}^{\ 2 \ 3 \ 4}}}-{�� \ {|_{\ 2 \ 6}^{\ 2 \ 3 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 2 \ 5}^{\ 2 \ 3 \ 6}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 2 \ 4}^{\ 2 \ 3 \ 7}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 2 \ 4}^{\ 2 \ 4 \ 0}}}-{�� \ {|_{\ 2 \ 5}^{\ 2 \ 4 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 2 \ 6}^{\ 2 \ 4 \ 2}}}-{�� \ {|_{\ 2 \ 7}^{\ 2 \ 4 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 2 \ 0}^{\ 2 \ 4 \ 4}}}+{{q_{2}}\ �� \ {|_{\ 2 \ 1}^{\ 2 \ 4 \ 5}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 2 \ 2}^{\ 2 \ 4 \ 6}}}+{{q_{2}}\ �� \ {|_{\ 2 \ 3}^{\ 2 \ 4 \ 7}}}+{�� \ {|_{\ 2 \ 5}^{\ 2 \ 5 \ 0}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 2 \ 4}^{\ 2 \ 5 \ 1}}}-{�� \ {|_{\ 2 \ 7}^{\ 2 \ 5 \ 2}}}+{�� \ {|_{\ 2 \ 6}^{\ 2 \ 5 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 2 \ 1}^{\ 2 \ 5 \ 4}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 2 \ 0}^{\ 2 \ 5 \ 5}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 3}^{\ 2 \ 5 \ 6}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 2}^{\ 2 \ 5 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 2 \ 6}^{\ 2 \ 6 \ 0}}}+{�� \ {|_{\ 2 \ 7}^{\ 2 \ 6 \ 1}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 2 \ 4}^{\ 2 \ 6 \ 2}}}-{�� \ {|_{\ 2 \ 5}^{\ 2 \ 6 \ 3}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 2 \ 2}^{\ 2 \ 6 \ 4}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 3}^{\ 2 \ 6 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 2 \ 0}^{\ 2 \ 6 \ 6}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 1}^{\ 2 \ 6 \ 7}}}+{�� \ {|_{\ 2 \ 7}^{\ 2 \ 7 \ 0}}}-{�� \ {|_{\ 2 \ 6}^{\ 2 \ 7 \ 1}}}+{�� \ {|_{\ 2 \ 5}^{\ 2 \ 7 \ 2}}}+ \
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 2 \ 4}^{\ 2 \ 7 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 2 \ 3}^{\ 2 \ 7 \ 4}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 2}^{\ 2 \ 7 \ 5}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 2 \ 1}^{\ 2 \ 7 \ 6}}}-{{q_{2}}\ �� \ {|_{\ 2 \ 0}^{\ 2 \ 7 \ 7}}}+{�� \ {|_{\ 3 \ 0}^{\ 3 \ 0 \ 0}}}+{�� \ {|_{\ 3 \ 1}^{\ 3 \ 0 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 3 \ 2}^{\ 3 \ 0 \ 2}}}+{�� \ {|_{\ 3 \ 3}^{\ 3 \ 0 \ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 3 \ 4}^{\ 3 \ 0 \ 4}}}+{�� \ {|_{\ 3 \ 5}^{\ 3 \ 0 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 3 \ 6}^{\ 3 \ 0 \ 6}}}+{�� \ {|_{\ 3 \ 7}^{\ 3 \ 0 \ 7}}}+{�� \ {|_{\ 3 \ 1}^{\ 3 \ 1 \ 0}}}-{�� \ {|_{\ 3 \ 0}^{\ 3 \ 1 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 3 \ 3}^{\ 3 \ 1 \ 2}}}-{�� \ {|_{\ 3 \ 2}^{\ 3 \ 1 \ 3}}}+{�� \ {|_{\ 3 \ 5}^{\ 3 \ 1 \ 4}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 3 \ 4}^{\ 3 \ 1 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 3 \ 7}^{\ 3 \ 1 \ 6}}}+{�� \ {|_{\ 3 \ 6}^{\ 3 \ 1 \ 7}}}+{�� \ {|_{\ 3 \ 2}^{\ 3 \ 2 \ 0}}}-{�� \ {|_{\ 3 \ 3}^{\ 3 \ 2 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 3 \ 0}^{\ 3 \ 2 \ 2}}}+{�� \ {|_{\ 3 \ 1}^{\ 3 \ 2 \ 3}}}+{�� \ {|_{\ 3 \ 6}^{\ 3 \ 2 \ 4}}}+{�� \ {|_{\ 3 \ 7}^{\ 3 \ 2 \ 5}}}-
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 3 \ 4}^{\ 3 \ 2 \ 6}}}-{�� \ {|_{\ 3 \ 5}^{\ 3 \ 2 \ 7}}}+{�� \ {|_{\ 3 \ 3}^{\ 3 \ 3 \ 0}}}+{�� \ {|_{\ 3 \ 2}^{\ 3 \ 3 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 3 \ 1}^{\ 3 \ 3 \ 2}}}-{�� \ {|_{\ 3 \ 0}^{\ 3 \ 3 \ 3}}}+{�� \ {|_{\ 3 \ 7}^{\ 3 \ 3 \ 4}}}-{�� \ {|_{\ 3 \ 6}^{\ 3 \ 3 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 3 \ 5}^{\ 3 \ 3 \ 6}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 3 \ 4}^{\ 3 \ 3 \ 7}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 3 \ 4}^{\ 3 \ 4 \ 0}}}-{�� \ {|_{\ 3 \ 5}^{\ 3 \ 4 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 3 \ 6}^{\ 3 \ 4 \ 2}}}-{�� \ {|_{\ 3 \ 7}^{\ 3 \ 4 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 3 \ 0}^{\ 3 \ 4 \ 4}}}+{{q_{2}}\ �� \ {|_{\ 3 \ 1}^{\ 3 \ 4 \ 5}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 3 \ 2}^{\ 3 \ 4 \ 6}}}+{{q_{2}}\ �� \ {|_{\ 3 \ 3}^{\ 3 \ 4 \ 7}}}+{�� \ {|_{\ 3 \ 5}^{\ 3 \ 5 \ 0}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 3 \ 4}^{\ 3 \ 5 \ 1}}}-{�� \ {|_{\ 3 \ 7}^{\ 3 \ 5 \ 2}}}+{�� \ {|_{\ 3 \ 6}^{\ 3 \ 5 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 3 \ 1}^{\ 3 \ 5 \ 4}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 3 \ 0}^{\ 3 \ 5 \ 5}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 3}^{\ 3 \ 5 \ 6}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 2}^{\ 3 \ 5 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 3 \ 6}^{\ 3 \ 6 \ 0}}}+{�� \ {|_{\ 3 \ 7}^{\ 3 \ 6 \ 1}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 3 \ 4}^{\ 3 \ 6 \ 2}}}-{�� \ {|_{\ 3 \ 5}^{\ 3 \ 6 \ 3}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 3 \ 2}^{\ 3 \ 6 \ 4}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 3}^{\ 3 \ 6 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 3 \ 0}^{\ 3 \ 6 \ 6}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 1}^{\ 3 \ 6 \ 7}}}+{�� \ {|_{\ 3 \ 7}^{\ 3 \ 7 \ 0}}}-{�� \ {|_{\ 3 \ 6}^{\ 3 \ 7 \ 1}}}+{�� \ {|_{\ 3 \ 5}^{\ 3 \ 7 \ 2}}}+ \
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 3 \ 4}^{\ 3 \ 7 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 3 \ 3}^{\ 3 \ 7 \ 4}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 2}^{\ 3 \ 7 \ 5}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 3 \ 1}^{\ 3 \ 7 \ 6}}}-{{q_{2}}\ �� \ {|_{\ 3 \ 0}^{\ 3 \ 7 \ 7}}}+{�� \ {|_{\ 4 \ 0}^{\ 4 \ 0 \ 0}}}+{�� \ {|_{\ 4 \ 1}^{\ 4 \ 0 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 4 \ 2}^{\ 4 \ 0 \ 2}}}+{�� \ {|_{\ 4 \ 3}^{\ 4 \ 0 \ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 4 \ 0 \ 4}}}+{�� \ {|_{\ 4 \ 5}^{\ 4 \ 0 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 4 \ 6}^{\ 4 \ 0 \ 6}}}+{�� \ {|_{\ 4 \ 7}^{\ 4 \ 0 \ 7}}}+{�� \ {|_{\ 4 \ 1}^{\ 4 \ 1 \ 0}}}-{�� \ {|_{\ 4 \ 0}^{\ 4 \ 1 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 4 \ 3}^{\ 4 \ 1 \ 2}}}-{�� \ {|_{\ 4 \ 2}^{\ 4 \ 1 \ 3}}}+{�� \ {|_{\ 4 \ 5}^{\ 4 \ 1 \ 4}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 4 \ 1 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 4 \ 7}^{\ 4 \ 1 \ 6}}}+{�� \ {|_{\ 4 \ 6}^{\ 4 \ 1 \ 7}}}+{�� \ {|_{\ 4 \ 2}^{\ 4 \ 2 \ 0}}}-{�� \ {|_{\ 4 \ 3}^{\ 4 \ 2 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 4 \ 0}^{\ 4 \ 2 \ 2}}}+{�� \ {|_{\ 4 \ 1}^{\ 4 \ 2 \ 3}}}+{�� \ {|_{\ 4 \ 6}^{\ 4 \ 2 \ 4}}}+{�� \ {|_{\ 4 \ 7}^{\ 4 \ 2 \ 5}}}-
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 4 \ 2 \ 6}}}-{�� \ {|_{\ 4 \ 5}^{\ 4 \ 2 \ 7}}}+{�� \ {|_{\ 4 \ 3}^{\ 4 \ 3 \ 0}}}+{�� \ {|_{\ 4 \ 2}^{\ 4 \ 3 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 4 \ 1}^{\ 4 \ 3 \ 2}}}-{�� \ {|_{\ 4 \ 0}^{\ 4 \ 3 \ 3}}}+{�� \ {|_{\ 4 \ 7}^{\ 4 \ 3 \ 4}}}-{�� \ {|_{\ 4 \ 6}^{\ 4 \ 3 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 4 \ 5}^{\ 4 \ 3 \ 6}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 4 \ 3 \ 7}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 4 \ 4 \ 0}}}-{�� \ {|_{\ 4 \ 5}^{\ 4 \ 4 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 4 \ 6}^{\ 4 \ 4 \ 2}}}-{�� \ {|_{\ 4 \ 7}^{\ 4 \ 4 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 4 \ 0}^{\ 4 \ 4 \ 4}}}+{{q_{2}}\ �� \ {|_{\ 4 \ 1}^{\ 4 \ 4 \ 5}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 4 \ 2}^{\ 4 \ 4 \ 6}}}+{{q_{2}}\ �� \ {|_{\ 4 \ 3}^{\ 4 \ 4 \ 7}}}+{�� \ {|_{\ 4 \ 5}^{\ 4 \ 5 \ 0}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 4 \ 5 \ 1}}}-{�� \ {|_{\ 4 \ 7}^{\ 4 \ 5 \ 2}}}+{�� \ {|_{\ 4 \ 6}^{\ 4 \ 5 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 4 \ 1}^{\ 4 \ 5 \ 4}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 4 \ 0}^{\ 4 \ 5 \ 5}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 4 \ 3}^{\ 4 \ 5 \ 6}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 4 \ 2}^{\ 4 \ 5 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 4 \ 6}^{\ 4 \ 6 \ 0}}}+{�� \ {|_{\ 4 \ 7}^{\ 4 \ 6 \ 1}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 4 \ 6 \ 2}}}-{�� \ {|_{\ 4 \ 5}^{\ 4 \ 6 \ 3}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 4 \ 2}^{\ 4 \ 6 \ 4}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 4 \ 3}^{\ 4 \ 6 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 4 \ 0}^{\ 4 \ 6 \ 6}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 4 \ 1}^{\ 4 \ 6 \ 7}}}+{�� \ {|_{\ 4 \ 7}^{\ 4 \ 7 \ 0}}}-{�� \ {|_{\ 4 \ 6}^{\ 4 \ 7 \ 1}}}+{�� \ {|_{\ 4 \ 5}^{\ 4 \ 7 \ 2}}}+ \
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4 \ 4}^{\ 4 \ 7 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 4 \ 3}^{\ 4 \ 7 \ 4}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 4 \ 2}^{\ 4 \ 7 \ 5}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 4 \ 1}^{\ 4 \ 7 \ 6}}}-{{q_{2}}\ �� \ {|_{\ 4 \ 0}^{\ 4 \ 7 \ 7}}}+{�� \ {|_{\ 5 \ 0}^{\ 5 \ 0 \ 0}}}+{�� \ {|_{\ 5 \ 1}^{\ 5 \ 0 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 2}^{\ 5 \ 0 \ 2}}}+{�� \ {|_{\ 5 \ 3}^{\ 5 \ 0 \ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 5 \ 4}^{\ 5 \ 0 \ 4}}}+{�� \ {|_{\ 5 \ 5}^{\ 5 \ 0 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 6}^{\ 5 \ 0 \ 6}}}+{�� \ {|_{\ 5 \ 7}^{\ 5 \ 0 \ 7}}}+{�� \ {|_{\ 5 \ 1}^{\ 5 \ 1 \ 0}}}-{�� \ {|_{\ 5 \ 0}^{\ 5 \ 1 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 3}^{\ 5 \ 1 \ 2}}}-{�� \ {|_{\ 5 \ 2}^{\ 5 \ 1 \ 3}}}+{�� \ {|_{\ 5 \ 5}^{\ 5 \ 1 \ 4}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 5 \ 4}^{\ 5 \ 1 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 5 \ 7}^{\ 5 \ 1 \ 6}}}+{�� \ {|_{\ 5 \ 6}^{\ 5 \ 1 \ 7}}}+{�� \ {|_{\ 5 \ 2}^{\ 5 \ 2 \ 0}}}-{�� \ {|_{\ 5 \ 3}^{\ 5 \ 2 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 5 \ 0}^{\ 5 \ 2 \ 2}}}+{�� \ {|_{\ 5 \ 1}^{\ 5 \ 2 \ 3}}}+{�� \ {|_{\ 5 \ 6}^{\ 5 \ 2 \ 4}}}+{�� \ {|_{\ 5 \ 7}^{\ 5 \ 2 \ 5}}}-
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 5 \ 4}^{\ 5 \ 2 \ 6}}}-{�� \ {|_{\ 5 \ 5}^{\ 5 \ 2 \ 7}}}+{�� \ {|_{\ 5 \ 3}^{\ 5 \ 3 \ 0}}}+{�� \ {|_{\ 5 \ 2}^{\ 5 \ 3 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 5 \ 1}^{\ 5 \ 3 \ 2}}}-{�� \ {|_{\ 5 \ 0}^{\ 5 \ 3 \ 3}}}+{�� \ {|_{\ 5 \ 7}^{\ 5 \ 3 \ 4}}}-{�� \ {|_{\ 5 \ 6}^{\ 5 \ 3 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 5}^{\ 5 \ 3 \ 6}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 5 \ 4}^{\ 5 \ 3 \ 7}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 5 \ 4}^{\ 5 \ 4 \ 0}}}-{�� \ {|_{\ 5 \ 5}^{\ 5 \ 4 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 5 \ 6}^{\ 5 \ 4 \ 2}}}-{�� \ {|_{\ 5 \ 7}^{\ 5 \ 4 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 5 \ 0}^{\ 5 \ 4 \ 4}}}+{{q_{2}}\ �� \ {|_{\ 5 \ 1}^{\ 5 \ 4 \ 5}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 5 \ 2}^{\ 5 \ 4 \ 6}}}+{{q_{2}}\ �� \ {|_{\ 5 \ 3}^{\ 5 \ 4 \ 7}}}+{�� \ {|_{\ 5 \ 5}^{\ 5 \ 5 \ 0}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 5 \ 4}^{\ 5 \ 5 \ 1}}}-{�� \ {|_{\ 5 \ 7}^{\ 5 \ 5 \ 2}}}+{�� \ {|_{\ 5 \ 6}^{\ 5 \ 5 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 5 \ 1}^{\ 5 \ 5 \ 4}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 5 \ 0}^{\ 5 \ 5 \ 5}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 5 \ 3}^{\ 5 \ 5 \ 6}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 5 \ 2}^{\ 5 \ 5 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 5 \ 6}^{\ 5 \ 6 \ 0}}}+{�� \ {|_{\ 5 \ 7}^{\ 5 \ 6 \ 1}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 5 \ 4}^{\ 5 \ 6 \ 2}}}-{�� \ {|_{\ 5 \ 5}^{\ 5 \ 6 \ 3}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 5 \ 2}^{\ 5 \ 6 \ 4}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 5 \ 3}^{\ 5 \ 6 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 5 \ 0}^{\ 5 \ 6 \ 6}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 5 \ 1}^{\ 5 \ 6 \ 7}}}+{�� \ {|_{\ 5 \ 7}^{\ 5 \ 7 \ 0}}}-{�� \ {|_{\ 5 \ 6}^{\ 5 \ 7 \ 1}}}+{�� \ {|_{\ 5 \ 5}^{\ 5 \ 7 \ 2}}}+ \
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 5 \ 4}^{\ 5 \ 7 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 5 \ 3}^{\ 5 \ 7 \ 4}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 5 \ 2}^{\ 5 \ 7 \ 5}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 5 \ 1}^{\ 5 \ 7 \ 6}}}-{{q_{2}}\ �� \ {|_{\ 5 \ 0}^{\ 5 \ 7 \ 7}}}+{�� \ {|_{\ 6 \ 0}^{\ 6 \ 0 \ 0}}}+{�� \ {|_{\ 6 \ 1}^{\ 6 \ 0 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 2}^{\ 6 \ 0 \ 2}}}+{�� \ {|_{\ 6 \ 3}^{\ 6 \ 0 \ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 6 \ 4}^{\ 6 \ 0 \ 4}}}+{�� \ {|_{\ 6 \ 5}^{\ 6 \ 0 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 6}^{\ 6 \ 0 \ 6}}}+{�� \ {|_{\ 6 \ 7}^{\ 6 \ 0 \ 7}}}+{�� \ {|_{\ 6 \ 1}^{\ 6 \ 1 \ 0}}}-{�� \ {|_{\ 6 \ 0}^{\ 6 \ 1 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 3}^{\ 6 \ 1 \ 2}}}-{�� \ {|_{\ 6 \ 2}^{\ 6 \ 1 \ 3}}}+{�� \ {|_{\ 6 \ 5}^{\ 6 \ 1 \ 4}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 6 \ 4}^{\ 6 \ 1 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 6 \ 7}^{\ 6 \ 1 \ 6}}}+{�� \ {|_{\ 6 \ 6}^{\ 6 \ 1 \ 7}}}+{�� \ {|_{\ 6 \ 2}^{\ 6 \ 2 \ 0}}}-{�� \ {|_{\ 6 \ 3}^{\ 6 \ 2 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 6 \ 0}^{\ 6 \ 2 \ 2}}}+{�� \ {|_{\ 6 \ 1}^{\ 6 \ 2 \ 3}}}+{�� \ {|_{\ 6 \ 6}^{\ 6 \ 2 \ 4}}}+{�� \ {|_{\ 6 \ 7}^{\ 6 \ 2 \ 5}}}-
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 6 \ 4}^{\ 6 \ 2 \ 6}}}-{�� \ {|_{\ 6 \ 5}^{\ 6 \ 2 \ 7}}}+{�� \ {|_{\ 6 \ 3}^{\ 6 \ 3 \ 0}}}+{�� \ {|_{\ 6 \ 2}^{\ 6 \ 3 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 6 \ 1}^{\ 6 \ 3 \ 2}}}-{�� \ {|_{\ 6 \ 0}^{\ 6 \ 3 \ 3}}}+{�� \ {|_{\ 6 \ 7}^{\ 6 \ 3 \ 4}}}-{�� \ {|_{\ 6 \ 6}^{\ 6 \ 3 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 5}^{\ 6 \ 3 \ 6}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 6 \ 4}^{\ 6 \ 3 \ 7}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 6 \ 4}^{\ 6 \ 4 \ 0}}}-{�� \ {|_{\ 6 \ 5}^{\ 6 \ 4 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 6 \ 6}^{\ 6 \ 4 \ 2}}}-{�� \ {|_{\ 6 \ 7}^{\ 6 \ 4 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 6 \ 0}^{\ 6 \ 4 \ 4}}}+{{q_{2}}\ �� \ {|_{\ 6 \ 1}^{\ 6 \ 4 \ 5}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 6 \ 2}^{\ 6 \ 4 \ 6}}}+{{q_{2}}\ �� \ {|_{\ 6 \ 3}^{\ 6 \ 4 \ 7}}}+{�� \ {|_{\ 6 \ 5}^{\ 6 \ 5 \ 0}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 6 \ 4}^{\ 6 \ 5 \ 1}}}-{�� \ {|_{\ 6 \ 7}^{\ 6 \ 5 \ 2}}}+{�� \ {|_{\ 6 \ 6}^{\ 6 \ 5 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 6 \ 1}^{\ 6 \ 5 \ 4}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 6 \ 0}^{\ 6 \ 5 \ 5}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 6 \ 3}^{\ 6 \ 5 \ 6}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 6 \ 2}^{\ 6 \ 5 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 6 \ 6}^{\ 6 \ 6 \ 0}}}+{�� \ {|_{\ 6 \ 7}^{\ 6 \ 6 \ 1}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 6 \ 4}^{\ 6 \ 6 \ 2}}}-{�� \ {|_{\ 6 \ 5}^{\ 6 \ 6 \ 3}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 6 \ 2}^{\ 6 \ 6 \ 4}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 6 \ 3}^{\ 6 \ 6 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 6 \ 0}^{\ 6 \ 6 \ 6}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 6 \ 1}^{\ 6 \ 6 \ 7}}}+{�� \ {|_{\ 6 \ 7}^{\ 6 \ 7 \ 0}}}-{�� \ {|_{\ 6 \ 6}^{\ 6 \ 7 \ 1}}}+{�� \ {|_{\ 6 \ 5}^{\ 6 \ 7 \ 2}}}+ \
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 6 \ 4}^{\ 6 \ 7 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 6 \ 3}^{\ 6 \ 7 \ 4}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 6 \ 2}^{\ 6 \ 7 \ 5}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 6 \ 1}^{\ 6 \ 7 \ 6}}}-{{q_{2}}\ �� \ {|_{\ 6 \ 0}^{\ 6 \ 7 \ 7}}}+{�� \ {|_{\ 7 \ 0}^{\ 7 \ 0 \ 0}}}+{�� \ {|_{\ 7 \ 1}^{\ 7 \ 0 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 2}^{\ 7 \ 0 \ 2}}}+{�� \ {|_{\ 7 \ 3}^{\ 7 \ 0 \ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 7 \ 4}^{\ 7 \ 0 \ 4}}}+{�� \ {|_{\ 7 \ 5}^{\ 7 \ 0 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 6}^{\ 7 \ 0 \ 6}}}+{�� \ {|_{\ 7 \ 7}^{\ 7 \ 0 \ 7}}}+{�� \ {|_{\ 7 \ 1}^{\ 7 \ 1 \ 0}}}-{�� \ {|_{\ 7 \ 0}^{\ 7 \ 1 \ 1}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 3}^{\ 7 \ 1 \ 2}}}-{�� \ {|_{\ 7 \ 2}^{\ 7 \ 1 \ 3}}}+{�� \ {|_{\ 7 \ 5}^{\ 7 \ 1 \ 4}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 7 \ 4}^{\ 7 \ 1 \ 5}}}-
\
\
\displaystyle
{�� \ {|_{\ 7 \ 7}^{\ 7 \ 1 \ 6}}}+{�� \ {|_{\ 7 \ 6}^{\ 7 \ 1 \ 7}}}+{�� \ {|_{\ 7 \ 2}^{\ 7 \ 2 \ 0}}}-{�� \ {|_{\ 7 \ 3}^{\ 7 \ 2 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 7 \ 0}^{\ 7 \ 2 \ 2}}}+{�� \ {|_{\ 7 \ 1}^{\ 7 \ 2 \ 3}}}+{�� \ {|_{\ 7 \ 6}^{\ 7 \ 2 \ 4}}}+{�� \ {|_{\ 7 \ 7}^{\ 7 \ 2 \ 5}}}-
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 7 \ 4}^{\ 7 \ 2 \ 6}}}-{�� \ {|_{\ 7 \ 5}^{\ 7 \ 2 \ 7}}}+{�� \ {|_{\ 7 \ 3}^{\ 7 \ 3 \ 0}}}+{�� \ {|_{\ 7 \ 2}^{\ 7 \ 3 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 7 \ 1}^{\ 7 \ 3 \ 2}}}-{�� \ {|_{\ 7 \ 0}^{\ 7 \ 3 \ 3}}}+{�� \ {|_{\ 7 \ 7}^{\ 7 \ 3 \ 4}}}-{�� \ {|_{\ 7 \ 6}^{\ 7 \ 3 \ 5}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 5}^{\ 7 \ 3 \ 6}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 7 \ 4}^{\ 7 \ 3 \ 7}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 7 \ 4}^{\ 7 \ 4 \ 0}}}-{�� \ {|_{\ 7 \ 5}^{\ 7 \ 4 \ 1}}}-
\
\
\displaystyle
{�� \ {|_{\ 7 \ 6}^{\ 7 \ 4 \ 2}}}-{�� \ {|_{\ 7 \ 7}^{\ 7 \ 4 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 7 \ 0}^{\ 7 \ 4 \ 4}}}+{{q_{2}}\ �� \ {|_{\ 7 \ 1}^{\ 7 \ 4 \ 5}}}+
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 7 \ 2}^{\ 7 \ 4 \ 6}}}+{{q_{2}}\ �� \ {|_{\ 7 \ 3}^{\ 7 \ 4 \ 7}}}+{�� \ {|_{\ 7 \ 5}^{\ 7 \ 5 \ 0}}}+
\
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 7 \ 4}^{\ 7 \ 5 \ 1}}}-{�� \ {|_{\ 7 \ 7}^{\ 7 \ 5 \ 2}}}+{�� \ {|_{\ 7 \ 6}^{\ 7 \ 5 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 7 \ 1}^{\ 7 \ 5 \ 4}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 7 \ 0}^{\ 7 \ 5 \ 5}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 7 \ 3}^{\ 7 \ 5 \ 6}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 7 \ 2}^{\ 7 \ 5 \ 7}}}+
\
\
\displaystyle
{�� \ {|_{\ 7 \ 6}^{\ 7 \ 6 \ 0}}}+{�� \ {|_{\ 7 \ 7}^{\ 7 \ 6 \ 1}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 7 \ 4}^{\ 7 \ 6 \ 2}}}-{�� \ {|_{\ 7 \ 5}^{\ 7 \ 6 \ 3}}}-
\
\
\displaystyle
{{q_{2}}\ �� \ {|_{\ 7 \ 2}^{\ 7 \ 6 \ 4}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 7 \ 3}^{\ 7 \ 6 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 7 \ 0}^{\ 7 \ 6 \ 6}}}-
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 7 \ 1}^{\ 7 \ 6 \ 7}}}+{�� \ {|_{\ 7 \ 7}^{\ 7 \ 7 \ 0}}}-{�� \ {|_{\ 7 \ 6}^{\ 7 \ 7 \ 1}}}+{�� \ {|_{\ 7 \ 5}^{\ 7 \ 7 \ 2}}}+ \
\
\displaystyle
{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 7 \ 4}^{\ 7 \ 7 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 7 \ 3}^{\ 7 \ 7 \ 4}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 7 \ 2}^{\ 7 \ 7 \ 5}}}+
\
\
\displaystyle
{�� \ {\overline{q_{2}}}\ {|_{\ 7 \ 1}^{\ 7 \ 7 \ 6}}}-{{q_{2}}\ �� \ {|_{\ 7 \ 0}^{\ 7 \ 7 \ 7}}}

(31)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

test(Hr = H )

$\label{eq32} \mbox{\rm false}$

(32)

Type: Boolean

fricas

Hl := (I,λ)/(Y,I);

                     2
                  + +
                  - --
                  +  2
                    +
   arity warning: ----
                     3
                  0 +
                  - --
                  0  2
                    +

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

test( Hl = H )

$\label{eq33} \mbox{\rm false}$

(33)

Type: Boolean

fricas

test( Hr = Hl )

$\label{eq34} \mbox{\rm false}$

(34)

Type: Boolean

Perhaps this is not too surprising since Octonion algebra is non-associative. Nevertheless Octonions are "Frobenius" in a more general sense because there is a non-degenerate associative pairing.

i = Unit of the algebra

fricas

i:=ⅇ.1

$\label{eq35}|_{\ 0}$

(35)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

test
         i     /
         λ     =    Ω

                  0 0
                  - -
                  + 0
   arity warning: ---
                  + 0
                  - -
                  + 0

$\label{eq36} \mbox{\rm false}$

(36)

Type: Boolean

Handle and handle element

fricas

Φ:ℒ :=
         λ     /
         X     /
         Y

                     2
                  0 +
                  - --
                  0  2
                    +
   arity warning: ----
                     2
                  0 +
                  - --
                  0  2
                    +

$\label{eq37}\begin{array}{@{}l} \displaystyle {�� \ {|_{\ 0}^{\ 0 \ 0}}}+{�� \ {|_{\ 1}^{\ 0 \ 1}}}+{�� \ {|_{\ 2}^{\ 0 \ 2}}}+{�� \ {|_{\ 3}^{\ 0 \ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 0 \ 4}}}+ \ \ \displaystyle {�� \ {|_{\ 5}^{\ 0 \ 5}}}+{�� \ {|_{\ 6}^{\ 0 \ 6}}}+{�� \ {|_{\ 7}^{\ 0 \ 7}}}+{�� \ {|_{\ 1}^{\ 1 \ 0}}}-{�� \ {|_{\ 0}^{\ 1 \ 1}}}-{�� \ {|_{\ 3}^{\ 1 \ 2}}}+ \ \ \displaystyle {�� \ {|_{\ 2}^{\ 1 \ 3}}}-{�� \ {|_{\ 5}^{\ 1 \ 4}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 1 \ 5}}}+{�� \ {|_{\ 7}^{\ 1 \ 6}}}-{�� \ {|_{\ 6}^{\ 1 \ 7}}}+ \ \ \displaystyle {�� \ {|_{\ 2}^{\ 2 \ 0}}}+{�� \ {|_{\ 3}^{\ 2 \ 1}}}-{�� \ {|_{\ 0}^{\ 2 \ 2}}}-{�� \ {|_{\ 1}^{\ 2 \ 3}}}-{�� \ {|_{\ 6}^{\ 2 \ 4}}}-{�� \ {|_{\ 7}^{\ 2 \ 5}}}+ \ \ \displaystyle {{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 2 \ 6}}}+{�� \ {|_{\ 5}^{\ 2 \ 7}}}+{�� \ {|_{\ 3}^{\ 3 \ 0}}}-{�� \ {|_{\ 2}^{\ 3 \ 1}}}+{�� \ {|_{\ 1}^{\ 3 \ 2}}}- \ \ \displaystyle {�� \ {|_{\ 0}^{\ 3 \ 3}}}-{�� \ {|_{\ 7}^{\ 3 \ 4}}}+{�� \ {|_{\ 6}^{\ 3 \ 5}}}-{�� \ {|_{\ 5}^{\ 3 \ 6}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 3 \ 7}}}+ \ \ \displaystyle {{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 4 \ 0}}}+{�� \ {|_{\ 5}^{\ 4 \ 1}}}+{�� \ {|_{\ 6}^{\ 4 \ 2}}}+{�� \ {|_{\ 7}^{\ 4 \ 3}}}-{{q_{2}}\ �� \ {|_{\ 0}^{\ 4 \ 4}}}- \ \ \displaystyle {{q_{2}}\ �� \ {|_{\ 1}^{\ 4 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 2}^{\ 4 \ 6}}}-{{q_{2}}\ �� \ {|_{\ 3}^{\ 4 \ 7}}}+{�� \ {|_{\ 5}^{\ 5 \ 0}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 5 \ 1}}}+ \ \ \displaystyle {�� \ {|_{\ 7}^{\ 5 \ 2}}}-{�� \ {|_{\ 6}^{\ 5 \ 3}}}+{{q_{2}}\ �� \ {|_{\ 1}^{\ 5 \ 4}}}-{{q_{2}}\ �� \ {|_{\ 0}^{\ 5 \ 5}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 3}^{\ 5 \ 6}}}- \ \ \displaystyle {�� \ {\overline{q_{2}}}\ {|_{\ 2}^{\ 5 \ 7}}}+{�� \ {|_{\ 6}^{\ 6 \ 0}}}-{�� \ {|_{\ 7}^{\ 6 \ 1}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 6 \ 2}}}+{�� \ {|_{\ 5}^{\ 6 \ 3}}}+ \ \ \displaystyle {{q_{2}}\ �� \ {|_{\ 2}^{\ 6 \ 4}}}-{�� \ {\overline{q_{2}}}\ {|_{\ 3}^{\ 6 \ 5}}}-{{q_{2}}\ �� \ {|_{\ 0}^{\ 6 \ 6}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 1}^{\ 6 \ 7}}}+{�� \ {|_{\ 7}^{\ 7 \ 0}}}+ \ \ \displaystyle {�� \ {|_{\ 6}^{\ 7 \ 1}}}-{�� \ {|_{\ 5}^{\ 7 \ 2}}}-{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 7 \ 3}}}+{{q_{2}}\ �� \ {|_{\ 3}^{\ 7 \ 4}}}+{�� \ {\overline{q_{2}}}\ {|_{\ 2}^{\ 7 \ 5}}}- \ \ \displaystyle {�� \ {\overline{q_{2}}}\ {|_{\ 1}^{\ 7 \ 6}}}-{{q_{2}}\ �� \ {|_{\ 0}^{\ 7 \ 7}}}$

(37)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

Φ1:=     i     /
         Φ

                   0 +
                   - -
                   + +
   arity warning: ----
                     2
                  0 +
                  - --
                  0  +

$\label{eq38}{�� \ {|_{\ 0}^{\ 0}}}+{�� \ {|_{\ 1}^{\ 1}}}+{�� \ {|_{\ 2}^{\ 2}}}+{�� \ {|_{\ 3}^{\ 3}}}+{{{{q_{2}}\ ��}\over{\overline{q_{2}}}}\ {|_{\ 4}^{\ 4}}}+{�� \ {|_{\ 5}^{\ 5}}}+{�� \ {|_{\ 6}^{\ 6}}}+{�� \ {|_{\ 7}^{\ 7}}}$

(38)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

Definition 5

Co-unit

  i 
  U

fricas

ι:ℒ:=
    (    i I    ) /
    (     Ų     )

                   + 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +

$\label{eq39}\begin{array}{@{}l} \displaystyle {�� \ {|_{\ 0 \ 0}^{\ 0}}}+{�� \ {|_{\ 0 \ 1}^{\ 1}}}+{�� \ {|_{\ 0 \ 2}^{\ 2}}}+{�� \ {|_{\ 0 \ 3}^{\ 3}}}+{�� \ {|_{\ 0 \ 4}^{\ 4}}}+{�� \ {|_{\ 0 \ 5}^{\ 5}}}+ \ \ \displaystyle {�� \ {|_{\ 0 \ 6}^{\ 6}}}+{�� \ {|_{\ 0 \ 7}^{\ 7}}}$

(39)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

Y=U
ι

fricas

test
        Y    /
        ι       = Ų

$\label{eq40} \mbox{\rm false}$

(40)

Type: Boolean

For example:

fricas

ex1:=[q[2]=1,p[1]=1]

$\label{eq41}\left[{{q_{2}}= 1}, \:{{p_{1}}= 1}\right]$

(41)

Type: List(Equation(Polynomial(Integer)))

fricas

Ų0:ℒ  :=eval(Ų,ex1)

$\label{eq42}��$

(42)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

Ω0:ℒ  :=eval(Ω,ex1)$ℒ

$\label{eq43}��$

(43)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

λ0:ℒ  :=eval(λ,ex1)$ℒ

$\label{eq44}��$

(44)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))

fricas

H0:ℒ :=eval(H,ex1)$ℒ

$\label{eq45}\begin{array}{@{}l} \displaystyle {�� \ {|_{\ 0}^{\ 0 \ 0}}}+{�� \ {|_{\ 1}^{\ 0 \ 1}}}+{�� \ {|_{\ 2}^{\ 0 \ 2}}}+{�� \ {|_{\ 3}^{\ 0 \ 3}}}+{�� \ {|_{\ 4}^{\ 0 \ 4}}}+{�� \ {|_{\ 5}^{\ 0 \ 5}}}+ \ \ \displaystyle {�� \ {|_{\ 6}^{\ 0 \ 6}}}+{�� \ {|_{\ 7}^{\ 0 \ 7}}}+{�� \ {|_{\ 1}^{\ 1 \ 0}}}-{�� \ {|_{\ 0}^{\ 1 \ 1}}}+{�� \ {|_{\ 3}^{\ 1 \ 2}}}-{�� \ {|_{\ 2}^{\ 1 \ 3}}}+ \ \ \displaystyle {�� \ {|_{\ 5}^{\ 1 \ 4}}}-{�� \ {|_{\ 4}^{\ 1 \ 5}}}-{�� \ {|_{\ 7}^{\ 1 \ 6}}}+{�� \ {|_{\ 6}^{\ 1 \ 7}}}+{�� \ {|_{\ 2}^{\ 2 \ 0}}}-{�� \ {|_{\ 3}^{\ 2 \ 1}}}- \ \ \displaystyle {�� \ {|_{\ 0}^{\ 2 \ 2}}}+{�� \ {|_{\ 1}^{\ 2 \ 3}}}+{�� \ {|_{\ 6}^{\ 2 \ 4}}}+{�� \ {|_{\ 7}^{\ 2 \ 5}}}-{�� \ {|_{\ 4}^{\ 2 \ 6}}}-{�� \ {|_{\ 5}^{\ 2 \ 7}}}+ \ \ \displaystyle {�� \ {|_{\ 3}^{\ 3 \ 0}}}+{�� \ {|_{\ 2}^{\ 3 \ 1}}}-{�� \ {|_{\ 1}^{\ 3 \ 2}}}-{�� \ {|_{\ 0}^{\ 3 \ 3}}}+{�� \ {|_{\ 7}^{\ 3 \ 4}}}-{�� \ {|_{\ 6}^{\ 3 \ 5}}}+ \ \ \displaystyle {�� \ {|_{\ 5}^{\ 3 \ 6}}}-{�� \ {|_{\ 4}^{\ 3 \ 7}}}+{�� \ {|_{\ 4}^{\ 4 \ 0}}}-{�� \ {|_{\ 5}^{\ 4 \ 1}}}-{�� \ {|_{\ 6}^{\ 4 \ 2}}}-{�� \ {|_{\ 7}^{\ 4 \ 3}}}- \ \ \displaystyle {�� \ {|_{\ 0}^{\ 4 \ 4}}}+{�� \ {|_{\ 1}^{\ 4 \ 5}}}+{�� \ {|_{\ 2}^{\ 4 \ 6}}}+{�� \ {|_{\ 3}^{\ 4 \ 7}}}+{�� \ {|_{\ 5}^{\ 5 \ 0}}}+{�� \ {|_{\ 4}^{\ 5 \ 1}}}- \ \ \displaystyle {�� \ {|_{\ 7}^{\ 5 \ 2}}}+{�� \ {|_{\ 6}^{\ 5 \ 3}}}-{�� \ {|_{\ 1}^{\ 5 \ 4}}}-{�� \ {|_{\ 0}^{\ 5 \ 5}}}-{�� \ {|_{\ 3}^{\ 5 \ 6}}}+{�� \ {|_{\ 2}^{\ 5 \ 7}}}+ \ \ \displaystyle {�� \ {|_{\ 6}^{\ 6 \ 0}}}+{�� \ {|_{\ 7}^{\ 6 \ 1}}}+{�� \ {|_{\ 4}^{\ 6 \ 2}}}-{�� \ {|_{\ 5}^{\ 6 \ 3}}}-{�� \ {|_{\ 2}^{\ 6 \ 4}}}+{�� \ {|_{\ 3}^{\ 6 \ 5}}}- \ \ \displaystyle {�� \ {|_{\ 0}^{\ 6 \ 6}}}-{�� \ {|_{\ 1}^{\ 6 \ 7}}}+{�� \ {|_{\ 7}^{\ 7 \ 0}}}-{�� \ {|_{\ 6}^{\ 7 \ 1}}}+{�� \ {|_{\ 5}^{\ 7 \ 2}}}+{�� \ {|_{\ 4}^{\ 7 \ 3}}}- \ \ \displaystyle {�� \ {|_{\ 3}^{\ 7 \ 4}}}-{�� \ {|_{\ 2}^{\ 7 \ 5}}}+{�� \ {|_{\ 1}^{\ 7 \ 6}}}-{�� \ {|_{\ 0}^{\ 7 \ 7}}}$

(45)

Type: ClosedLinearOperator(OrderedVariableList([0,1,2,3,4,5,6,7]),Expression(Integer))