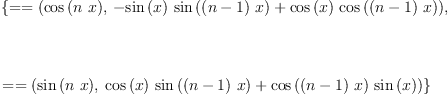MathAction Manipulating Expressions

Topics

FrontPage
- FAQ
  - FriCAS Problems
    - Manipulating Expressions <-- You are here.

SandBoxDomainOfComputation

The domain InputForm can be quite useful for manipulating parts of expressions. For example

fricas

(1) -> ex1:=integrate(log(x)+x, x)

$\label{eq1}\frac{{2 \ x \ {\log \left({x}\right)}}+{{x}^{2}}-{2 \ x}}{2}$

(1)

Type: Union(Expression(Integer),...)

fricas

)set output tex off

fricas

)set output algebra on

%::InputForm

   (2)  (/ (+ (* (* 2 x) (log x)) (+ (^ x 2) (* - 2 x))) 2)

Type: InputForm

fricas

)set output tex on

fricas

)set output algebra off

ex2:=interpret((%::InputForm).2.2)

$\label{eq2}2 \ x \ {\log \left({x}\right)}$

(2)

Type: Expression(Integer)

If you would like to do this with a more common type of expression and hide the details, you can define

fricas

op(n,x) == interpret((x::InputForm).(n+1))

Type: Void

Then manipulating expressions looks like this:

fricas

op(1,ex1)

fricas

Compiling function op with type (PositiveInteger, Expression(Integer
      )) -> Any

$\label{eq3}{2 \ x \ {\log \left({x}\right)}}+{{x}^{2}}-{2 \ x}$

(3)

Type: Expression(Integer)

fricas

op(1,%)

fricas

Compiling function op with type (PositiveInteger, Any) -> Any

$\label{eq4}2 \ x \ {\log \left({x}\right)}$

(4)

Type: Expression(Integer)

fricas

(op(1,op(1,ex1))-op(2,op(1,ex1)))/op(2,ex1)

$\label{eq5}\frac{{2 \ x \ {\log \left({x}\right)}}-{{x}^{2}}+{2 \ x}}{2}$

(5)

Type: Expression(Integer)

Rules and Pattern Matching (from WesterProblemSet)

Trigonometric manipulations---these are typically difficult for students

fricas

r:= cos(3*x)/cos(x)

$\label{eq6}\frac{\cos \left({3 \ x}\right)}{\cos \left({x}\right)}$

(6)

Type: Expression(Integer)

=> cos(x)^2 - 3 sin(x)^2 or similar

fricas

real(complexNormalize(r))

$\label{eq7}-{2 \ {{\sin \left({x}\right)}^{2}}}+{2 \ {{\cos \left({x}\right)}^{2}}}- 1$

(7)

Type: Expression(Integer)

=> 2 cos(2 x) - 1

fricas

real(normalize(simplify(complexNormalize(r))))

$\label{eq8}{2 \ {\cos \left({2 \ x}\right)}}- 1$

(8)

Type: Expression(Integer)

Use rewrite rules => cos(x)^2 - 3 sin(x)^2

fricas

sincosAngles:= rule
   cos((n | integer?(n)) * x) ==
      cos((n - 1)*x) * cos(x) - sin((n - 1)*x) * sin(x)
   sin((n | integer?(n)) * x) ==
      sin((n - 1)*x) * cos(x) + cos((n - 1)*x) * sin(x)

$\label{eq9}\begin{array}{@{}l} \displaystyle \left\{{= = \left({{\cos \left({n \ x}\right)}, \:{-{{\sin \left({x}\right)}\ {\sin \left({{\left(n - 1 \right)}\ x}\right)}}+{{\cos \left({x}\right)}\ {\cos \left({{\left(n - 1 \right)}\ x}\right)}}}}\right)}, \right. \ \ \displaystyle \left.\: \right. \ \ \displaystyle \left.{= = \left({{\sin \left({n \ x}\right)}, \:{{{\cos \left({x}\right)}\ {\sin \left({{\left(n - 1 \right)}\ x}\right)}}+{{\cos \left({{\left(n - 1 \right)}\ x}\right)}\ {\sin \left({x}\right)}}}}\right)}\right\}$

(9)

Type: Ruleset(Integer,Integer,Expression(Integer))

fricas

sincosAngles r

$\label{eq10}-{3 \ {{\sin \left({x}\right)}^{2}}}+{{\cos \left({x}\right)}^{2}}$

(10)

Type: Expression(Integer)

Other Operations

The domain FunctionSpace? includes the following operations:

    isExpt(p,f:Symbol) returns [x, n] if p = x^n and n <> 0 and x = f(a)
    isExpt(p,op:BasicOperator) returns [x, n] if p = x^n and n <> 0 and x = op(a)
    isExpt(p) returns [x, n] if p = x^n and n <> 0
    isMult(p) returns [n, x] if p = n * x and n <> 0
    isPlus(p) returns [m1,...,mn] if p = m1 +...+ mn and n > 1
    isPower(p) returns [x, n] if p = x^n and n <> 0
    isTimes(p) returns [a1,...,an] if p = a1*...*an and n > 1

If these conditions are not met, then the above operations return "failed".

For example,

fricas

isMult(3*x)

   There are 1 exposed and 0 unexposed library operations named isMult 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                             )display op isMult
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named 
      isMult with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

but

fricas

isMult(x*y)

   There are 1 exposed and 0 unexposed library operations named isMult 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                             )display op isMult
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named 
      isMult with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

In the context of Expression Integer, or Polynomial Integer the parameter n must be an Integer. The Symbol y is not an Integer.

Not exactly analogously

fricas

isPower(x^y)

$\label{eq11}\left[{val ={{x}^{y}}}, \:{exponent = 1}\right]$

(11)

Type: Union(Record(val: Expression(Integer),exponent: Integer),...)

whereas

fricas

isPower(x^10)

   There are 1 exposed and 2 unexposed library operations named isPower
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                             )display op isPower
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named 
      isPower with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

In the first case the Integer is assume to be 1.

We have:

fricas

isTimes(x*y*z)

$\label{eq12}\left[ z , \: y , \: x \right]$

(12)

Type: Union(List(Polynomial(Integer)),...)

fricas

isPlus(x+y+z*y)

$\label{eq13}\left[{y \ z}, \: y , \: x \right]$

(13)

Type: Union(List(Polynomial(Integer)),...)

Whereas

fricas

isTimes((x+y)*z)

$\label{eq14}\verb#"failed"#$

(14)

Type: Union("failed",...)

That is because the expression is internally treated as a MultivariatePolynomial like this:

fricas

((x+y)*z)::MPOLY([x,y,z],INT)

$\label{eq15}{z \ x}+{z \ y}$

(15)

Type: MultivariatePolynomial?([x,y,z],Integer)

If you say:

fricas

isPlus((x+y)*z)

$\label{eq16}\left[{y \ z}, \:{x \ z}\right]$

(16)

Type: Union(List(Polynomial(Integer)),...)

perhaps the result makes sense?

For some of the details of these operations I consulted the actual algebra code at:

http://axiom-wiki.newsynthesis.org/axiom--test--1/src/algebra/FspaceSpad

Click on pdf or dvi to see the documentation.

You can also enter expressions like isTimes in the search box on the upper right and see all the places in the algebra where this operation is defined and used.

Subject: Be Bold !!

	( 15 subscribers )