References
See also:
An n-dimensional algebra is represented by a (2,1)-tensor
 viewed as a linear operator with two inputs
viewed as a linear operator with two inputs  and one
output
and one
output  . For example in 2 dimensions
. For example in 2 dimensions
axiom
n:=2
axiom
T:=CartesianTensor(1,n,FRAC POLY INT)
Type: Type
axiom
Y:T := unravel(concat concat
[[[script(y,[[i,j],[k]])
for i in 1..n]
for j in 1..n]
for k in 1..n]
)
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
Given two vectors  and
and 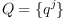
axiom
P:T := unravel([script(p,[[],[i]]) for i in 1..n])
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
axiom
Q:T := unravel([script(q,[[],[i]]) for i in 1..n])
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
the tensor  operates on their tensor product to
yield a vector
operates on their tensor product to
yield a vector 
axiom
R:=contract(contract(Y,3,product(P,Q),1),2,3)
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
Pictorially:
P Q
Y
R
or more explicitly
Pi Qj
\/
\
Rk
In Axiom we may use the more convenient tensor inner
product denoted by * that combines tensor product with
a contraction on the last index of the first tensor and
the first index of the second tensor.
axiom
R:=(Y*P)*Q
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
An algebra is said to be associative if:
Y = Y
Y Y
Note: the right hand side of the equation above is
implicitly the mirror image of the left hand side:
i j k i j k i j k
\ | / \/ / \ \/
\ | / \ / \ /
\|/ = e k - i e
| \/ \/
| \ /
l l l
This requires that the following (3,1)-tensor
(associator) is zero.
axiom
YY := reindex(reindex(Y,[1,3,2])*reindex(Y,[1,3,2]),[1,4,3,2])-Y*Y; ravel(YY)
Type: List(Fraction(Polynomial(Integer)))
The algebra  is commutative if:
is commutative if:
Y = Y
i j i j j i
\ / = \/ - \/
| \ /
k k k
This requires that the following (2,1)-tensor
(commutator) is zero.
axiom
YC:=Y-reindex(Y,[1,3,2])
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
A basis for the ideal defined by the coefficients of the
commutator is given by:
axiom
groebner(ravel(YC))
Type: List(Polynomial(Integer))
The algebra  is anti-commutative if:
is anti-commutative if:
Y = -Y
i j i j j i
\ / = \/ = \/
| \ /
k k k
This requires that the following (2,1)-tensor
(anti-commutator) is zero.
axiom
YA:=Y+reindex(Y,[1,3,2])
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
A basis for the ideal defined by the coefficients of the
commutator is given by:
axiom
groebner(ravel(YA))
Type: List(Polynomial(Integer))
The Jacobi identity is:
X
Y = Y + Y
Y Y Y
i j k i j k i j k i j k
\ | / \ / / \ \ / \ \ /
\ | / \ / / \ \ / \ 0
\ | / \/ / \ \/ \/ \
\ | / \ / \ / \ \
\|/ = e k - i e - e j
| \/ \/ \/
| \ / /
l l l l
An algebra satisfies the Jacobi identity if and only if
the following (3,1)-tensor
is zero.
axiom
YX := YY - reindex(contract(Y,1,Y,2),[3,1,4,2]); ravel(YX)
Type: List(Fraction(Polynomial(Integer)))
A scalar product is denoted by the (2,0)-tensor

axiom
U:T := unravel(concat
[[script(u,[[],[j,i]])
for i in 1..n]
for j in 1..n]
)
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
Definition 1
We say that the scalar product is associative if the tensor
equation holds:
Y = Y
U U
In other words, if the (3,0)-tensor:
i j k i j k i j k
\ | / \/ / \ \/
\|/ = \ / - \ /
0 0 0
(three-point function) is zero.
axiom
YU := reindex(reindex(U,[2,1])*reindex(Y,[1,3,2]),[3,2,1])-U*Y
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
Definition 2
An algebra with a non-degenerate associative scalar product
is called pre-Frobenius.
We may consider the problem where multiplication Y is given,
and look for all associative scalar products  or we
may consider an scalar product U as given, and look for all
algebras
or we
may consider an scalar product U as given, and look for all
algebras  such that the scalar product is associative.
such that the scalar product is associative.
This problem can be solved using linear algebra.
axiom
)expose MCALCFN
MultiVariableCalculusFunctions is now explicitly exposed in frame
initial
K := jacobian(ravel(YU),concat(map(variables,ravel(Y)))::List Symbol);
Type: Matrix(Fraction(Polynomial(Integer)))
axiom
yy := transpose matrix [concat(map(variables,ravel(Y)))::List Symbol];
Type: Matrix(Polynomial(Integer))
axiom
K::OutputForm * yy::OutputForm = 0
Type: Equation(OutputForm
?)
The matrix K transforms the coefficients of the tensor  into coefficients of the tensor
into coefficients of the tensor  . We are looking for
coefficients of the tensor
. We are looking for
coefficients of the tensor  such that
such that K transforms the
tensor  into
into  for any
for any  .
.
A necessary condition for the equation to have a non-trivial
solution is that the matrix K be degenerate.
Theorem 1
All 2-dimensional pre-Frobenius algebras are symmetric.
Proof: Consider the determinant of the matrix K above.
axiom
Kd := factor(determinant(K)::DMP(concat map(variables,ravel(U)),FRAC INT))
Type: Factored(DistributedMultivariatePolynomial
?([*002u11,
*002u12,
*002u21,
*002u22],
Fraction(Integer)))
The scalar product must also be non-degenerate
axiom
Ud:DMP(concat map(variables,ravel(U)),FRAC INT) := determinant [[U[i,j] for j in 1..n] for i in 1..n]
Type: DistributedMultivariatePolynomial
?([*002u11,
*002u12,
*002u21,
*002u22],
Fraction(Integer))
therefore U must be symmetric.
axiom
nthFactor(Kd,1)
Type: DistributedMultivariatePolynomial
?([*002u11,
*002u12,
*002u21,
*002u22],
Fraction(Integer))
axiom
US:T := unravel(map(x+->subst(x,U[2,1]=U[1,2]),ravel U))
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
Theorem 2
All 2-dimensional algebras with associative scalar product
are commutative.
Proof: The basis of the null space of the symmetric
K matrix are all symmetric
axiom
YUS:T := reindex(reindex(US,[2,1])*reindex(Y,[1,3,2]),[3,2,1])-US*Y
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
axiom
KS := jacobian(ravel(YUS),concat(map(variables,ravel(Y)))::List Symbol);
Type: Matrix(Fraction(Polynomial(Integer)))
axiom
NS:=nullSpace(KS)
Type: List(Vector(Fraction(Polynomial(Integer))))
axiom
SS:=map((x,y)+->x=y,concat map(variables,ravel Y),
entries reduce(+,[p[i]*NS.i for i in 1..#NS]))
Type: List(Equation(Fraction(Polynomial(Integer))))
axiom
YS:T := unravel(map(x+->subst(x,SS),ravel Y))
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
This defines a 4-parameter family of 2-d pre-Frobenius algebras
axiom
test(unravel(map(x+->subst(x,SS),ravel YUS))$T=0*YU)
Type: Boolean
Alternatively we may consider
axiom
J := jacobian(ravel(YU),concat(map(variables,ravel(U)))::List Symbol);
Type: Matrix(Fraction(Polynomial(Integer)))
axiom
uu := transpose matrix [concat(map(variables,ravel(U)))::List Symbol];
Type: Matrix(Polynomial(Integer))
axiom
J::OutputForm * uu::OutputForm = 0
Type: Equation(OutputForm
?)
The matrix J transforms the coefficients of the tensor  into coefficients of the tensor
into coefficients of the tensor  . We are looking for
coefficients of the tensor
. We are looking for
coefficients of the tensor  such that
such that J transforms the
tensor  into
into  for any
for any  .
.
A necessary condition for the equation to have a non-trivial
solution is that all 70 of the 4x4 sub-matrices of J are
degenerate. To this end we can form the polynomial ideal of
the determinants of these sub-matrices.
axiom
JP:=ideal concat concat concat
[[[[ determinant(
matrix([row(J,i1),row(J,i2),row(J,i3),row(J,i4)]))
for i4 in (i3+1)..maxRowIndex(J) ]
for i3 in (i2+1)..(maxRowIndex(J)-1) ]
for i2 in (i1+1)..(maxRowIndex(J)-2) ]
for i1 in minRowIndex(J)..(maxRowIndex(J)-3) ];
Type: PolynomialIdeal
?(Fraction(Integer),
IndexedExponents
?(Symbol),
Symbol,
Polynomial(Fraction(Integer)))
axiom
#generators(%)
Theorem 3
If a 2-d algebra is associative, commutative, anti-commutative
or if it satisfies the Jacobi identity then it is a
pre-Frobenius algebra.
Proof
Consider the ideals of the associator, commutator, anti-commutator
and Jacobi identity
axiom
YYI:=ideal ravel YY;
Type: PolynomialIdeal
?(Fraction(Integer),
IndexedExponents
?(Symbol),
Symbol,
Polynomial(Fraction(Integer)))
axiom
in?(JP,YYI) -- associative
Type: Boolean
axiom
YCI:=ideal ravel YC;
Type: PolynomialIdeal
?(Fraction(Integer),
IndexedExponents
?(Symbol),
Symbol,
Polynomial(Fraction(Integer)))
axiom
in?(JP,YCI) -- commutative
Type: Boolean
axiom
YAI:=ideal ravel YA;
Type: PolynomialIdeal
?(Fraction(Integer),
IndexedExponents
?(Symbol),
Symbol,
Polynomial(Fraction(Integer)))
axiom
in?(JP,YAI) -- anti-commutative
Type: Boolean
axiom
YXI:=ideal ravel YX;
Type: PolynomialIdeal
?(Fraction(Integer),
IndexedExponents
?(Symbol),
Symbol,
Polynomial(Fraction(Integer)))
axiom
in?(JP,YXI) -- Jacobi identity
Type: Boolean
Y-forms
Three traces of two graftings of an algebra gives six
(2,0)-forms.
Left snail and right snail:
LS RS
Y /\ /\ Y
Y ) ( Y
\/ \/
i j j i
\/ \/
\ /\ /\ /
e f \ / f e
\/ \ / \/
\ / \ /
f / \ f
\/ \/
axiom
LS:=contract(Y*Y,1,2)
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
axiom
RS:=reindex(contract(reindex(Y,[1,3,2])*reindex(Y,[1,3,2]),1,2),[2,1])
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
axiom
test(LS=RS)
Type: Boolean
Left and right deer:
RD LD
\ /\/ \/\ /
Y /\ /\ Y
Y ) ( Y
\/ \/
i j i j
\ /\ / \ /\ /
\ f \ / \ / f /
\/ \/ \/ \/
\ /\ /\ /
e / \ / \ e
\/ \ / \/
\ / \ /
f / \ f
\/ \/
Left and right deer forms are identical but different from snails.
axiom
RD:=contract(Y*Y,1,3)
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
axiom
LD:=reindex(contract(reindex(Y,[1,3,2])*reindex(Y,[1,3,2]),1,3),[2,1])
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
axiom
test(LD=RD)
Type: Boolean
axiom
test(RD=RS)
Type: Boolean
axiom
test(RD=LS)
Type: Boolean
Left and right turtles:
RT LT
/\ / / \ \ /\
( Y / \ Y )
\ Y Y /
\/ \/
i j i j
/\ / / \ \ /\
/ f / / \ \ f \
/ \/ / \ \/ \
\ \ / \ / /
\ e / \ e /
\ \/ \/ /
\ / \ /
\ f f /
\/ \/
axiom
RT:=contract(Y*Y,1,4)
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
axiom
LT:=reindex(contract(reindex(Y,[1,3,2])*reindex(Y,[1,3,2]),1,4),[2,1])
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
axiom
test(LT=RT)
Type: Boolean
The turles are symmetric
axiom
test(RT=reindex(RT,[2,1]))
Type: Boolean
axiom
test(LT=reindex(LT,[2,1]))
Type: Boolean
Five of the six forms are independent.
axiom
test(RT=RS)
Type: Boolean
axiom
test(RT=LS)
Type: Boolean
axiom
test(RT=RD)
Type: Boolean
axiom
test(LT=RS)
Type: Boolean
axiom
test(LT=LS)
Type: Boolean
axiom
test(LT=RD)
Type: Boolean
Associativity implies right turtle equals right snail
and left turtle equals left snail.
axiom
in?(ideal ravel(RT-RS),YYI)
Type: Boolean
axiom
in?(ideal ravel(LT-LS),YYI)
Type: Boolean
If the Jacobi identity holds then both snails are zero
axiom
in?(ideal ravel(RS),YXI)
Type: Boolean
axiom
in?(ideal ravel(LS),YXI)
Type: Boolean
and right turtle and deer have opposite signs
axiom
in?(ideal ravel(RT+RD),YXI)
Type: Boolean
![]() viewed as a linear operator with two inputs
viewed as a linear operator with two inputs ![]() and one
output
and one
output ![]() . For example in 2 dimensions
. For example in 2 dimensions

![]() and
and ![]()
![]() operates on their tensor product to
yield a vector
operates on their tensor product to
yield a vector ![]()
![\label{eq6}\begin{array}{@{}l}
\displaystyle
\left[{{{p^{2}}\ {q^{2}}\ {y_{2, \: 2}^{1}}}+{{p^{2}}\ {q^{1}}\ {y_{2, \: 1}^{1}}}+{{p^{1}}\ {q^{2}}\ {y_{1, \: 2}^{1}}}+{{p^{1}}\ {q^{1}}\ {y_{1, \: 1}^{1}}}}, \: \right.
\
\
\displaystyle
\left.{{{p^{2}}\ {q^{2}}\ {y_{2, \: 2}^{2}}}+{{p^{2}}\ {q^{1}}\ {y_{2, \: 1}^{2}}}+{{p^{1}}\ {q^{2}}\ {y_{1, \: 2}^{2}}}+{{p^{1}}\ {q^{1}}\ {y_{1, \: 1}^{2}}}}\right]
\label{eq6}\begin{array}{@{}l}
\displaystyle
\left[{{{p^{2}}\ {q^{2}}\ {y_{2, \: 2}^{1}}}+{{p^{2}}\ {q^{1}}\ {y_{2, \: 1}^{1}}}+{{p^{1}}\ {q^{2}}\ {y_{1, \: 2}^{1}}}+{{p^{1}}\ {q^{1}}\ {y_{1, \: 1}^{1}}}}, \: \right.
\
\
\displaystyle
\left.{{{p^{2}}\ {q^{2}}\ {y_{2, \: 2}^{2}}}+{{p^{2}}\ {q^{1}}\ {y_{2, \: 1}^{2}}}+{{p^{1}}\ {q^{2}}\ {y_{1, \: 2}^{2}}}+{{p^{1}}\ {q^{1}}\ {y_{1, \: 1}^{2}}}}\right]](images/8734404072350308678-16.0px.png)
![\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[{{{p^{2}}\ {q^{2}}\ {y_{2, \: 2}^{1}}}+{{p^{2}}\ {q^{1}}\ {y_{2, \: 1}^{1}}}+{{p^{1}}\ {q^{2}}\ {y_{1, \: 2}^{1}}}+{{p^{1}}\ {q^{1}}\ {y_{1, \: 1}^{1}}}}, \: \right.
\
\
\displaystyle
\left.{{{p^{2}}\ {q^{2}}\ {y_{2, \: 2}^{2}}}+{{p^{2}}\ {q^{1}}\ {y_{2, \: 1}^{2}}}+{{p^{1}}\ {q^{2}}\ {y_{1, \: 2}^{2}}}+{{p^{1}}\ {q^{1}}\ {y_{1, \: 1}^{2}}}}\right]
\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[{{{p^{2}}\ {q^{2}}\ {y_{2, \: 2}^{1}}}+{{p^{2}}\ {q^{1}}\ {y_{2, \: 1}^{1}}}+{{p^{1}}\ {q^{2}}\ {y_{1, \: 2}^{1}}}+{{p^{1}}\ {q^{1}}\ {y_{1, \: 1}^{1}}}}, \: \right.
\
\
\displaystyle
\left.{{{p^{2}}\ {q^{2}}\ {y_{2, \: 2}^{2}}}+{{p^{2}}\ {q^{1}}\ {y_{2, \: 1}^{2}}}+{{p^{1}}\ {q^{2}}\ {y_{1, \: 2}^{2}}}+{{p^{1}}\ {q^{1}}\ {y_{1, \: 1}^{2}}}}\right]](images/5969066627286587503-16.0px.png)
![\label{eq9}\begin{array}{@{}l}
\displaystyle
\left[{-{{y_{1, \: 1}^{2}}\ {y_{2, \: 1}^{1}}}+{{y_{1, \: 1}^{2}}\ {y_{1, \: 2}^{1}}}}, \:{{{y_{1, \: 1}^{2}}\ {y_{2, \: 2}^{1}}}-{{y_{2, \: 1}^{1}}\ {y_{2, \: 1}^{2}}}}, \right.
\
\
\displaystyle
\left.\:{{{y_{1, \: 2}^{1}}\ {y_{2, \: 1}^{2}}}+{{\left(-{y_{1, \: 2}^{2}}+{y_{1, \: 1}^{1}}\right)}\ {y_{2, \: 1}^{1}}}-{{y_{1, \: 1}^{1}}\ {y_{1, \: 2}^{1}}}}, \: \right.
\
\
\displaystyle
\left.{-{{y_{2, \: 1}^{1}}\ {y_{2, \: 2}^{2}}}+{{\left({y_{2, \: 1}^{2}}-{y_{1, \: 1}^{1}}\right)}\ {y_{2, \: 2}^{1}}}+{{y_{2, \: 1}^{1}}^2}}, \: \right.
\
\
\displaystyle
\left.{-{{y_{1, \: 1}^{2}}\ {y_{2, \: 2}^{1}}}+{{y_{1, \: 2}^{1}}\ {y_{1, \: 2}^{2}}}}, \:{{\left(-{y_{2, \: 1}^{2}}+{y_{1, \: 2}^{2}}\right)}\ {y_{2, \: 2}^{1}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{1, \: 2}^{1}}\ {y_{2, \: 2}^{2}}}+{{\left(-{y_{1, \: 2}^{2}}+{y_{1, \: 1}^{1}}\right)}\ {y_{2, \: 2}^{1}}}-{{y_{1, \: 2}^{1}}^2}}, \: \right.
\
\
\displaystyle
\left.{{\left({y_{2, \: 1}^{1}}-{y_{1, \: 2}^{1}}\right)}\ {y_{2, \: 2}^{1}}}, \:{-{{y_{1, \: 1}^{2}}\ {y_{2, \: 1}^{2}}}+{{y_{1, \: 1}^{2}}\ {y_{1, \: 2}^{2}}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{1, \: 1}^{2}}\ {y_{2, \: 2}^{2}}}-{{y_{2, \: 1}^{2}}^2}+{{y_{1, \: 1}^{1}}\ {y_{2, \: 1}^{2}}}-{{y_{1, \: 1}^{2}}\ {y_{2, \: 1}^{1}}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{1, \: 1}^{2}}\ {y_{2, \: 1}^{1}}}-{{y_{1, \: 1}^{2}}\ {y_{1, \: 2}^{1}}}}, \:{-{{y_{1, \: 1}^{2}}\ {y_{2, \: 2}^{1}}}+{{y_{2, \: 1}^{1}}\ {y_{2, \: 1}^{2}}}}, \right.
\
\
\displaystyle
\left.\:{-{{y_{1, \: 1}^{2}}\ {y_{2, \: 2}^{2}}}+{{y_{1, \: 2}^{2}}^2}-{{y_{1, \: 1}^{1}}\ {y_{1, \: 2}^{2}}}+{{y_{1, \: 1}^{2}}\ {y_{1, \: 2}^{1}}}}, \: \right.
\
\
\displaystyle
\left.{{{\left(-{y_{2, \: 1}^{2}}+{y_{1, \: 2}^{2}}\right)}\ {y_{2, \: 2}^{2}}}+{{y_{1, \: 2}^{1}}\ {y_{2, \: 1}^{2}}}-{{y_{1, \: 2}^{2}}\ {y_{2, \: 1}^{1}}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{1, \: 1}^{2}}\ {y_{2, \: 2}^{1}}}-{{y_{1, \: 2}^{1}}\ {y_{1, \: 2}^{2}}}}, \:{{\left({y_{2, \: 1}^{2}}-{y_{1, \: 2}^{2}}\right)}\ {y_{2, \: 2}^{1}}}\right]
\label{eq9}\begin{array}{@{}l}
\displaystyle
\left[{-{{y_{1, \: 1}^{2}}\ {y_{2, \: 1}^{1}}}+{{y_{1, \: 1}^{2}}\ {y_{1, \: 2}^{1}}}}, \:{{{y_{1, \: 1}^{2}}\ {y_{2, \: 2}^{1}}}-{{y_{2, \: 1}^{1}}\ {y_{2, \: 1}^{2}}}}, \right.
\
\
\displaystyle
\left.\:{{{y_{1, \: 2}^{1}}\ {y_{2, \: 1}^{2}}}+{{\left(-{y_{1, \: 2}^{2}}+{y_{1, \: 1}^{1}}\right)}\ {y_{2, \: 1}^{1}}}-{{y_{1, \: 1}^{1}}\ {y_{1, \: 2}^{1}}}}, \: \right.
\
\
\displaystyle
\left.{-{{y_{2, \: 1}^{1}}\ {y_{2, \: 2}^{2}}}+{{\left({y_{2, \: 1}^{2}}-{y_{1, \: 1}^{1}}\right)}\ {y_{2, \: 2}^{1}}}+{{y_{2, \: 1}^{1}}^2}}, \: \right.
\
\
\displaystyle
\left.{-{{y_{1, \: 1}^{2}}\ {y_{2, \: 2}^{1}}}+{{y_{1, \: 2}^{1}}\ {y_{1, \: 2}^{2}}}}, \:{{\left(-{y_{2, \: 1}^{2}}+{y_{1, \: 2}^{2}}\right)}\ {y_{2, \: 2}^{1}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{1, \: 2}^{1}}\ {y_{2, \: 2}^{2}}}+{{\left(-{y_{1, \: 2}^{2}}+{y_{1, \: 1}^{1}}\right)}\ {y_{2, \: 2}^{1}}}-{{y_{1, \: 2}^{1}}^2}}, \: \right.
\
\
\displaystyle
\left.{{\left({y_{2, \: 1}^{1}}-{y_{1, \: 2}^{1}}\right)}\ {y_{2, \: 2}^{1}}}, \:{-{{y_{1, \: 1}^{2}}\ {y_{2, \: 1}^{2}}}+{{y_{1, \: 1}^{2}}\ {y_{1, \: 2}^{2}}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{1, \: 1}^{2}}\ {y_{2, \: 2}^{2}}}-{{y_{2, \: 1}^{2}}^2}+{{y_{1, \: 1}^{1}}\ {y_{2, \: 1}^{2}}}-{{y_{1, \: 1}^{2}}\ {y_{2, \: 1}^{1}}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{1, \: 1}^{2}}\ {y_{2, \: 1}^{1}}}-{{y_{1, \: 1}^{2}}\ {y_{1, \: 2}^{1}}}}, \:{-{{y_{1, \: 1}^{2}}\ {y_{2, \: 2}^{1}}}+{{y_{2, \: 1}^{1}}\ {y_{2, \: 1}^{2}}}}, \right.
\
\
\displaystyle
\left.\:{-{{y_{1, \: 1}^{2}}\ {y_{2, \: 2}^{2}}}+{{y_{1, \: 2}^{2}}^2}-{{y_{1, \: 1}^{1}}\ {y_{1, \: 2}^{2}}}+{{y_{1, \: 1}^{2}}\ {y_{1, \: 2}^{1}}}}, \: \right.
\
\
\displaystyle
\left.{{{\left(-{y_{2, \: 1}^{2}}+{y_{1, \: 2}^{2}}\right)}\ {y_{2, \: 2}^{2}}}+{{y_{1, \: 2}^{1}}\ {y_{2, \: 1}^{2}}}-{{y_{1, \: 2}^{2}}\ {y_{2, \: 1}^{1}}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{1, \: 1}^{2}}\ {y_{2, \: 2}^{1}}}-{{y_{1, \: 2}^{1}}\ {y_{1, \: 2}^{2}}}}, \:{{\left({y_{2, \: 1}^{2}}-{y_{1, \: 2}^{2}}\right)}\ {y_{2, \: 2}^{1}}}\right]](images/4144419458590850645-16.0px.png)
![]() is commutative if:
is commutative if:

![]() is anti-commutative if:
is anti-commutative if:


![]()

![]() or we
may consider an scalar product U as given, and look for all
algebras
or we
may consider an scalar product U as given, and look for all
algebras ![]() such that the scalar product is associative.
such that the scalar product is associative. 
![]() into coefficients of the tensor
into coefficients of the tensor ![]() . We are looking for
coefficients of the tensor
. We are looking for
coefficients of the tensor ![]() such that
such that ![]() into
into ![]() for any
for any ![]() .
.
![\label{eq27}\begin{array}{@{}l}
\displaystyle
\left[{\left[{{{u^{1, \: 1}}^2}\over{{u^{1, \: 2}}^2}}, \:{{u^{1, \: 1}}\over{u^{1, \: 2}}}, \:{{u^{1, \: 1}}\over{u^{1, \: 2}}}, \: 1, \: 0, \: 0, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ -{{u^{2, \: 2}}\over{u^{1, \: 2}}}, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[{{-{{u^{1, \: 1}}\ {u^{2, \: 2}}}+{{u^{1, \: 2}}^2}}\over{{u^{1, \: 2}}^2}}, \: -{{u^{2, \: 2}}\over{u^{1, \: 2}}}, \: -{{u^{2, \: 2}}\over{u^{1, \: 2}}}, \: 0, \: 0, \: 1, \: 1, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[{{u^{1, \: 1}}\over{u^{1, \: 2}}}, \: 1, \: 1, \: 0, \: 0, \: 0, \: 0, \: 1 \right]}\right]
\label{eq27}\begin{array}{@{}l}
\displaystyle
\left[{\left[{{{u^{1, \: 1}}^2}\over{{u^{1, \: 2}}^2}}, \:{{u^{1, \: 1}}\over{u^{1, \: 2}}}, \:{{u^{1, \: 1}}\over{u^{1, \: 2}}}, \: 1, \: 0, \: 0, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ -{{u^{2, \: 2}}\over{u^{1, \: 2}}}, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[{{-{{u^{1, \: 1}}\ {u^{2, \: 2}}}+{{u^{1, \: 2}}^2}}\over{{u^{1, \: 2}}^2}}, \: -{{u^{2, \: 2}}\over{u^{1, \: 2}}}, \: -{{u^{2, \: 2}}\over{u^{1, \: 2}}}, \: 0, \: 0, \: 1, \: 1, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[{{u^{1, \: 1}}\over{u^{1, \: 2}}}, \: 1, \: 1, \: 0, \: 0, \: 0, \: 0, \: 1 \right]}\right]](images/2409629627165335235-16.0px.png)



![]() into coefficients of the tensor
into coefficients of the tensor ![]() . We are looking for
coefficients of the tensor
. We are looking for
coefficients of the tensor ![]() such that
such that ![]() into
into ![]() for any
for any ![]() .
.




