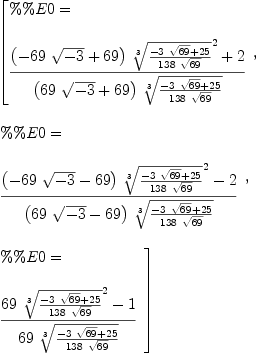fricas (1) -> f := x/(x^3-x+1)
Type: Fraction(Polynomial(Integer))
fricas )set output tex off fricas )set output algebra on Type: Union(Expression(Integer),
fricas )set output tex on fricas )set output algebra off
Type: Expression(Integer)
fricas ks := kernels i
Type: List(Kernel(Expression(Integer)))
fricas [definingPolynomial(k::Expression(Integer)) for k in ks | name operator k = 'rootOf]
Type: List(Expression(Integer))
fricas definingPolynomial(%%E0)
Type: Expression(Integer)
fricas s:=radicalSolve(%::Fraction Polynomial Integer)
Type: List(Equation(Expression(Integer)))
fricas i0 := integrate(f,
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas eval(i0, Type: Expression(Integer)
fricas complexNumeric %
Type: Complex(Float)
fricas eval(i0, Type: Expression(Integer)
fricas complexNumeric %
Type: Complex(Float)
fricas eval(i0, Type: Expression(Integer)
fricas complexNumeric %
Type: Complex(Float)
|
|
|
|
last edited 3 years ago by page |
![\label{eq3}\begin{array}{@{}l}
\displaystyle
\left[{\log{\left({{{\left({{207}\ \%\%E 0}+{23}\right)}\ {\sqrt{\frac{-{{69}\ {{\%\%E 0}^{2}}}- 4}{23}}}}-{{207}\ {{\%\%E 0}^{2}}}+{{2
3}\ \%\%E 0}+{{50}\ x}- 6}\right)}}, \right.
\
\
\displaystyle
\left.\: \right.
\
\
\displaystyle
\left.{\log{\left({{{\left(-{{207}\ \%\%E 0}-{23}\right)}\ {\sqrt{\frac{-{{69}\ {{\%\%E 0}^{2}}}- 4}{23}}}}-{{207}\ {{\%\%E 0}^{2}}}+{{2
3}\ \%\%E 0}+{{50}\ x}- 6}\right)}}, \right.
\
\
\displaystyle
\left.\:{\sqrt{\frac{-{{69}\ {{\%\%E 0}^{2}}}- 4}{23}}}, \: \right.
\
\
\displaystyle
\left.{\log \left({{{207}\ {{\%\%E 0}^{2}}}-{{23}\ \%\%E 0}+{{25}\ x}+ 6}\right)}, \: \%\%E 0 \right]
\label{eq3}\begin{array}{@{}l}
\displaystyle
\left[{\log{\left({{{\left({{207}\ \%\%E 0}+{23}\right)}\ {\sqrt{\frac{-{{69}\ {{\%\%E 0}^{2}}}- 4}{23}}}}-{{207}\ {{\%\%E 0}^{2}}}+{{2
3}\ \%\%E 0}+{{50}\ x}- 6}\right)}}, \right.
\
\
\displaystyle
\left.\: \right.
\
\
\displaystyle
\left.{\log{\left({{{\left(-{{207}\ \%\%E 0}-{23}\right)}\ {\sqrt{\frac{-{{69}\ {{\%\%E 0}^{2}}}- 4}{23}}}}-{{207}\ {{\%\%E 0}^{2}}}+{{2
3}\ \%\%E 0}+{{50}\ x}- 6}\right)}}, \right.
\
\
\displaystyle
\left.\:{\sqrt{\frac{-{{69}\ {{\%\%E 0}^{2}}}- 4}{23}}}, \: \right.
\
\
\displaystyle
\left.{\log \left({{{207}\ {{\%\%E 0}^{2}}}-{{23}\ \%\%E 0}+{{25}\ x}+ 6}\right)}, \: \%\%E 0 \right]](images/917962505280268211-16.0px.png)
![\label{eq4}\left[{\frac{{{23}\ {{\%\%E 0}^{3}}}+ \%\%E 0 + 1}{23}}\right]
\label{eq4}\left[{\frac{{{23}\ {{\%\%E 0}^{3}}}+ \%\%E 0 + 1}{23}}\right]](images/4664885149604351609-16.0px.png)