Calculations in character Hopf algebras using SCHUR and Maple
Symmetric functions provide a tool for computations in invariant
theory and especially for group characters. Recently, developments in Hopf algebra
have pushed forward these technologies to cope with a wide class of subgroups of
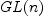 . To be able to provide examples computer algebra computations are
inevitable due to the inherent combinatorial complexity of the problem. We
describe how SCHUR (B.G. Wybourne et al.)
was used to compute characters of non-semisimple groups and what its benefits
and deficiencies are. Furthermore we discuss the Maple package
SchurFkt? (R. Ablamowicz, B. Fauser)
which was designed to provide a proof-of-concept approach for new algorithms.
Problems with data structures, efficiency etc. will be addressed.
. To be able to provide examples computer algebra computations are
inevitable due to the inherent combinatorial complexity of the problem. We
describe how SCHUR (B.G. Wybourne et al.)
was used to compute characters of non-semisimple groups and what its benefits
and deficiencies are. Furthermore we discuss the Maple package
SchurFkt? (R. Ablamowicz, B. Fauser)
which was designed to provide a proof-of-concept approach for new algorithms.
Problems with data structures, efficiency etc. will be addressed.