help links subscribe changes refresh edit

	IssueTracker
#298 undesirable horizontal scroll bar ←	↑	→ #3 )cd directory does not work in Windows version 0.1

#299 MachineFloat is not a FIeld

Edit detail for #299 MachineFloat is not a FIeld revision 2 of 2

	1 2
Editor: kratt6 Time: 2007/12/28 13:41:07 GMT-8
Note:

added:

From kratt6 Fri Dec 28 13:41:07 -0800 2007
From: kratt6
Date: Fri, 28 Dec 2007 13:41:07 -0800
Subject: 
Message-ID: <20071228134107-0800@axiom-wiki.newsynthesis.org>

Category: Axiom Mathematics => Axiom Library

fricas

(1) -> F := MachineFloat

$\label{eq1}\hbox{\axiomType{MachineFloat}\ }$

(1)

Type: Type

fricas

a: F := -0.12345

$\label{eq2}-{0.12345}$

(2)

Type: MachineFloat?

fricas

b: F := -1234567890.0

$\label{eq3}-{1234567890.0}$

(3)

Type: MachineFloat?

fricas

c: F := 1234567890.12345

$\label{eq4}1234567890.12345$

(4)

Type: MachineFloat?

fricas

(a+b)+c

$\label{eq5}-{0.2384185791 \<u> 015625 E - 6}$

(5)

Type: MachineFloat?

fricas

a+(b+c)

$\label{eq6}-{0.1976013183 \<u> 496717 E - 6}$

(6)

Type: MachineFloat?

fricas

F has Field

$\label{eq7} \mbox{\rm true}$

(7)

Type: Boolean

MachineFloat? clearly doesn't form a (mathematical) field as the above code demonstrates (and we all know).

DoubleFloat? and Float too --greg, Thu, 22 Jun 2006 09:18:32 -0500 reply

fricas

)cl all

   All user variables and function definitions have been cleared.
F := Float

$\label{eq8}\hbox{\axiomType{Float}\ }$

(8)

Type: Type

fricas

digits()

$\label{eq9}20$

(9)

Type: PositiveInteger?

fricas

a: F := -0.12345

$\label{eq10}-{0.12345}$

(10)

Type: Float

fricas

b: F := -1234567890.0

$\label{eq11}-{12 \<u> 34567890.0}$

(11)

Type: Float

fricas

c: F := 1234567890.12345

$\label{eq12}1234567890.12345$

(12)

Type: Float

fricas

(a+b)+c

$\label{eq13}0.0$

(13)

Type: Float

fricas

a+(b+c)

$\label{eq14}-{0.861473381 E - 12}$

(14)

Type: Float

fricas

F has Field

$\label{eq15} \mbox{\rm true}$

(15)

Type: Boolean

Axiom is not very strict... --kratt6, Thu, 22 Jun 2006 09:39:26 -0500 reply

Unfortunately, Axiom is not very strict with these things, although it should be, I believe. Some examples:

in Axiom, every field has the attribute canonicalUnitNormal.

In ATTREG.SPAD, we find:

  canonicalUnitNormal
    ++ \spad{canonicalUnitNormal} is true if we can choose a canonical
    ++ representative for each class of associate elements, that is
    ++ \spad{associates?(a,b)} returns true if and only if 
    ++ \spad{unitCanonical(a) = unitCanonical(b)}.

However, I suspect, this cannot be done in every field.

the domain EXPR is a field, although it is (I think) meant to allow arbitrary functions to be expressed, for example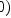 $\chi(x<0)$ , which does not have an inverse, I'd say.

In the documentation of MuPAD?, they say that (their) expression domain is a field for "convenience". Maybe this is related to the above.

In any case, we certainly cannot decide whether an element is zero or not.

Martin

... --kratt6, Fri, 28 Dec 2007 13:41:07 -0800 reply

Category: Axiom Mathematics => Axiom Library