help links subscribe changes refresh edit

	FrontPage
TouchGraph ←	↑	→ TypedGcd

TypeTowerDemo

Edit detail for TypeTowerDemo revision 1 of 5

	1 2 3 4 5
Editor: hemmecke Time: 2008/08/18 11:33:58 GMT-7
Note:

changed:
-
This page demonstrates some features of Axiom.

Let's begin with the construction of a polynomial ring $R$ in the indeterminate $z$
with coefficients from the ring $S$ of square matrices with entries that are
polynomials $P=F[x]$ where $F$ is the Galois field with 3 elements.
\begin{axiom}
F:= PrimeField 3
P:=UnivariatePolynomial(x, F)
S := SquareMatrix(2, P)
R := UnivariatePolynomial(z, S) 
\end{axiom}

OK, now we have the type $R$. Let's construct an element.
We start with constructing some coefficients first.
\begin{axiom}
s1:S := matrix[[2*x +1 ,x^2-1],[0,x-1]]
s2 := transpose s1
\end{axiom}

And now we build the polynomial.
\begin{axiom}
r: R := z^2 + s1*z + s2
\end{axiom}

Of course, since we work in characteristic 3, the following sum must be zero.
\begin{axiom}
r+ 2*r
\end{axiom}
Note that this is not the integer 0, but it is still a polynomial of type $R$.

Asking for the degree of $r$ is no problem, because $R$ is a univariate polynomial ring.
\begin{axiom}
degree r
\end{axiom}

So let's see what happens if we multiply $r$ by itself.
\begin{axiom}
r2 := r*r
\end{axiom}

Well, of course there is a common factor of $r_2$ an $r$. Can Axiom find it?
\begin{axiom}
gcd(r2, r)
\end{axiom}
Ooops. What does that say?::

  Cannot find a definition or applicable library operation named gcd.

Ah, of course, the coefficient ring of $R$ is the matrix ring $S$ and this is
unfortunately not an integral domain. So Axiom simply stops by telling you that
there is no applicaple operation.

Of course, Axiom can compute a gcd of univariate polynomials.
\begin{axiom}
p1:=s1(1,1)
p2:=s1(1,2)
gcd(p1,p2)
\end{axiom}

OK, let us do that again.
\begin{axiom}
q1: UP(x, INT) := 2*x+1
q2: UP(x, INT) := x^2+2
gcd(q1,q2)
\end{axiom}

Nice! Depending on where I compute these polynomials either
have a common factor or are coprime.

Well, all depends on the underlying ring, of course.

This page demonstrates some features of Axiom.

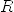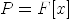Let's begin with the construction of a polynomial ring in the indeterminate with coefficients from the ring of square matrices with entries that are polynomials where 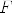is the Galois field with 3 elements.

axiom

F:= PrimeField 3

(1)

Type: Domain

axiom

P:=UnivariatePolynomial(x, F)

(2)

Type: Domain

axiom

S := SquareMatrix(2, P)

(3)

Type: Domain

axiom

R := UnivariatePolynomial(z, S)

(4)

Type: Domain

OK, now we have the type 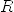. Let's construct an element. We start with constructing some coefficients first.

axiom

s1:S := matrix[[2*x +1 ,x^2-1],[0,x-1]]

(5)

Type: SquareMatrix?(2,UnivariatePolynomial?(x,PrimeField? 3))

axiom

s2 := transpose s1

(6)

Type: SquareMatrix?(2,UnivariatePolynomial?(x,PrimeField? 3))

And now we build the polynomial.

axiom

r: R := z^2 + s1*z + s2

(7)

Type: UnivariatePolynomial?(z,SquareMatrix?(2,UnivariatePolynomial?(x,PrimeField? 3)))

Of course, since we work in characteristic 3, the following sum must be zero.

axiom

r+ 2*r

(8)

Type: UnivariatePolynomial?(z,SquareMatrix?(2,UnivariatePolynomial?(x,PrimeField? 3)))

Note that this is not the integer 0, but it is still a polynomial of type .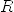

Asking for the degree of is no problem, because 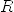is a univariate polynomial ring.

axiom

degree r

(9)

Type: PositiveInteger?

So let's see what happens if we multiply by itself.

axiom

r2 := r*r

(10)

Type: UnivariatePolynomial?(z,SquareMatrix?(2,UnivariatePolynomial?(x,PrimeField? 3)))

Well, of course there is a common factor of an . Can Axiom find it?

axiom

gcd(r2, r)

   There are 4 exposed and 3 unexposed library operations named gcd
      having 2 argument(s) but none was determined to be applicable.
      Use HyperDoc Browse, or issue
                               )display op gcd
      to learn more about the available operations. Perhaps
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named gcd
      with argument type(s)
UnivariatePolynomial(z,SquareMatrix(2,UnivariatePolynomial(x,PrimeField 3)))
UnivariatePolynomial(z,SquareMatrix(2,UnivariatePolynomial(x,PrimeField 3)))

      Perhaps you should use "@" to indicate the required return type,
      or "$" to specify which version of the function you need.

Ooops. What does that say?:

  Cannot find a definition or applicable library operation named gcd.

Ah, of course, the coefficient ring of 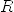is the matrix ring and this is unfortunately not an integral domain. So Axiom simply stops by telling you that there is no applicaple operation.

Of course, Axiom can compute a gcd of univariate polynomials.

axiom