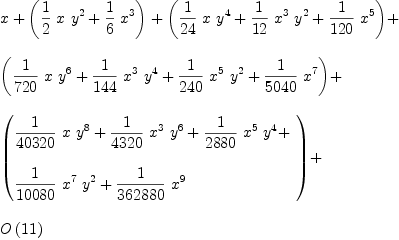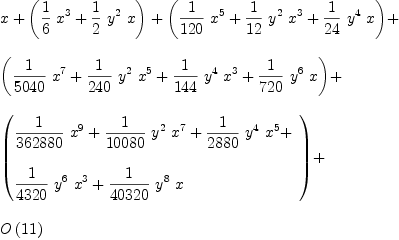Example for multivariate Taylor series expansion
Univariate TaylorSeries
FriCAS? can deal with power series in a simple manner.
fricas
x:=taylor 'x
Type: UnivariateTaylorSeries
?(Expression(Integer),
x,
0)
fricas
sinh(x)
Type: UnivariateTaylorSeries
?(Expression(Integer),
x,
0)
However, sometimes one wants to be more precise with the domain
that the object lives in. If, for example, we don't want power
series over the general expression domain as exemplified above,
we can give the coefficient domain explicitly.
fricas
Z ==> Integer
Type: Void
fricas
Q ==> Fraction Z
Type: Void
fricas
Ux ==> UnivariateTaylorSeries(Q, 'x, 0)
Type: Void
fricas
ux: Ux := 'x
Type: UnivariateTaylorSeries
?(Fraction(Integer),
x,
0)
fricas
sinh(ux)
Type: UnivariateTaylorSeries
?(Fraction(Integer),
x,
0)
Combination of univariate TaylorSeries
The FriCAS? interpreter is smart enough to create an appropriate
type if two univariate Taylor series interact.
However, as seen below, the resulting domain is something like
i.e., univariate power series in y with coefficients that are
univariate power series in x that have rational coefficients.
fricas
Uy ==> UnivariateTaylorSeries(Q, 'y, 0)
Type: Void
fricas
uy: Uy := 'y
Type: UnivariateTaylorSeries
?(Fraction(Integer),
y,
0)
fricas
cosh(uy)
Type: UnivariateTaylorSeries
?(Fraction(Integer),
y,
0)
fricas
sinh(ux)*cosh(uy)
Type: UnivariateTaylorSeries
?(UnivariateTaylorSeries
?(Fraction(Integer),
x,
0),
y,
0)
As a general rule, the FriCAS? interpreter tries to find
a "better coefficient domain" if something does not fit
into the type of the current object in order to construct
a more general domain that can hold the result of the operation.
In the case above that is probably not what we expected or wanted.
Multivariate TaylorSeries in infinitely many variables
There is a domain in FriCAS? that is similar to the Polynomial(Q) domain.
TaylorSeries(Q) is the domain of power series over Q in infinitely
many variables.
With that domain the input is as simple as for univariate power series.
fricas
T ==> TaylorSeries Q
Type: Void
fricas
tx:T := 'x
Type: TaylorSeries
?(Fraction(Integer))
fricas
ty:T := 'y
Type: TaylorSeries
?(Fraction(Integer))
fricas
sinh(tx)*cosh(ty)
Type: TaylorSeries
?(Fraction(Integer))
Multivariate TaylorSeries in two variables
FriCAS? allows to be more precise with multivariate power series.
It is possible to create multivariate power series in a given
number of variables. Such a construction is, however, a bit more
involved.
The domain (named M below') is modelled as a univariate power series
over bivariate polynomials where the n-th coefficient of the series is
the polynomial consisting of all (bivariate) terms of degree n.
Thus we first have to create a bivariate polynomial domain.
From this construction, it should be clear how to create multivariate
series in three or more variables.
fricas
vl: List Symbol := ['x, 'y]
Type: List(Symbol)
fricas
V ==> OrderedVariableList vl
Type: Void
fricas
P ==> SparseMultivariatePolynomial(Q, V)
Type: Void
fricas
M ==> SparseMultivariateTaylorSeries(Q, V, P)
Type: Void
fricas
X: M := monomial(1$M, 'x, 1)
Type: SparseMultivariateTaylorSeries
?(Fraction(Integer),
OrderedVariableList
?([x,
y]),
SparseMultivariatePolynomial
?(Fraction(Integer),
OrderedVariableList
?([x,
y])))
fricas
Y: M := monomial(1$M, 'y, 1)
Type: SparseMultivariateTaylorSeries
?(Fraction(Integer),
OrderedVariableList
?([x,
y]),
SparseMultivariatePolynomial
?(Fraction(Integer),
OrderedVariableList
?([x,
y])))
fricas
sinh(X)*cosh(Y)
Type: SparseMultivariateTaylorSeries
?(Fraction(Integer),
OrderedVariableList
?([x,
y]),
SparseMultivariatePolynomial
?(Fraction(Integer),
OrderedVariableList
?([x,
y])))