|
A hash table implementation via double hashing
author Ralf Hemmecke
original source dated 14-Sep-2012
Abstract
A hash table domain is implemented. Hash tables are like arrays in the
sense that they allow to insert/extract/delete an element in almost
constant time.
Revision
Modified by Bill Page to allow user specified equality.
Overview
We implement a hash table domain that uses a double hashing strategy.
The main idea is as follows. An extensible array of buckets is used to
store key/entry pairs where the index is computed using a hash
function. If two keys happen to have the same hash value 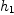 , i.e.,
another key/entry pair would have to be stored in the same bucket, a
second hash function is employed to compute another value , i.e.,
another key/entry pair would have to be stored in the same bucket, a
second hash function is employed to compute another value 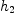 . Then . Then
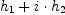 modulo the array size is used to look for another
free bucket by increasing modulo the array size is used to look for another
free bucket by increasing 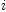 . .
With double hashing it is important to have a special distinct value
that marks an unused vacant bucket. Furthermore, because of the way
the entries are stored via double hashing, deletion of an entry can
just happen by overriding the position with a distinct marker. Thus a
second distinct value is necessary that marks a bucket that has once
been filled but whose value has subsequently been deleted. We call
these marker values VACANT' and DELETED,
respectively. VACANT and DELETED should not be part
of the key space.
Let's assume that the type of the marker values is Marker.
Naively, and type correctly, we would have to use as representation
like the following:
Union(Marker, Record(key: Key, entry: Entry))
Of course, for efficiency reasons that is undesirable. For storing
one new key/entry pair, we would have to allocate memory in order to
form the record and another allocation to form the union of the
markers and pairs. Therefore, we assume that markers keys and entries
all need the same amount of memory (which is basically the size of a
pointer) and store markers, keys, and entries in a flat way.
Keys are distinguished from entries by storing keys only in the first
half of the array and entries in the second half. Markers can only
appear in the first half of the array (instead of a key). If the index
corresponding to a key is 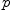 and and 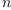 is half the size of the
array, then the entry corresponding to the key is stored at index is half the size of the
array, then the entry corresponding to the key is stored at index 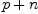 . .
A type in FriCAS that can hold a pointer is None. However,
since None is actually a technical domain that does not have
any inhabitants and is not expressing our idea logically, we introduce
a type UMKE to stand for Union(Marker, Key, Entry) and
represent it by None. For efficiency reasons, UMKE
and its coercions from/to the respective domains will be implemented
via macros.
fricas (1) -> <spad>
fricas )abbrev domain XHASHTBL XHashTable
rep x ==> (x@%) pretend Rep
per x ==> (x@Rep) pretend %
N ==> NonNegativeInteger
Z ==> Integer
I ==> SingleInteger
B ==> Boolean
++ Author: Ralf Hemmecke
++ Keywords: hash table
++ Description:
++ An implementation of a hash table that uses equality of the key domain
++ or a user specified function to decide upon equality of keys.
XHashTable(Key: SetCategory, Entry: Type):
Join(TableAggregate(Key, Entry), finiteAggregate, shallowlyMutable) with
table: (Key -> SingleInteger) -> %
++ table(h) creates an empty hash table that uses h instead of
++ hash$Key. Note that h should be a mathematical function in
++ the sense that from k1=k2 follows h(k1)=h(k2). If that is not
++ the case, k1 and k2 will internally be considered as being
++ different keys.
table: (Key -> SingleInteger,(Key,Key) -> Boolean) -> %
++ table(h,eq) creates an empty hash table that uses eq instead
++ of the "=" from the Key domain. Note that h and eq must be
++ compatible in the sense that h(k1)~=h(k2) -> not eq(k1,k2)
== add
KE ==> Record(key: Key, entry: Entry)
UE ==> Union(Entry, "failed")
Marker ==> None
toMarker mk ==> mk@Marker -- note that MKey==Marker==UMKE
VACANT : Marker := (HASHTABLEVACANT$Lisp) pretend Marker -- pos never used
DELETED: Marker := (HASHTABLEDELETED$Lisp) pretend Marker -- pos is deleted
vacant?(mk) ==> EQ(toMarker mk, VACANT)$Lisp
deleted?(mk) ==> EQ(toMarker mk, DELETED)$Lisp
key?(mk) ==> not (vacant? mk or deleted? mk)
MKey ==> None
UMKE ==> None
Buckets ==> PrimitiveArray UMKE
numOfBuckets(a) ==> shift(#a, -1)
toUMKE x ==> x pretend UMKE
toKey k ==> (k@UMKE) pretend Key
getMKey(a, i) ==> ((a.i)@UMKE) pretend MKey
setKey!(a, i, k) ==> (a.i := toUMKE k) pretend Key
getEntry(a, n, i) ==> a(n+i) pretend Entry
setEntry!(a, n, i, e) ==> (a(n+i) := toUMKE e) pretend Entry
setKeyEntry!(a, n, i, k, e) ==> (setKey!(a, i, k); setEntry!(a, n, i, e))
-- deleteKeyEntry!(a, n, i) ==> setKeyEntry!(a, n, i, DELETED, VACANT)
deleteKeyEntry!(a, n, i) ==>
(a.i := toUMKE DELETED; a(n+i) := toUMKE VACANT)
maxLoad n ==> n*7 quo 10 -- load factor
maxVirtualLoad n ==> n*9 quo 10 -- virtual load factor
arrayLengths: PrimitiveArray N := [[_
7, 13, 31, 61, 109, 241, 463, 1021, 2029, 4093, 8089, 16363,_
32719, 65521, 131011, 262111, 524221, 1048573, 2097133,_
4193803, 8388451, 16777141, 33554011, 67108669, 134217439,_
268435009, 536870839, 1073741719, 2147482951, 4294965841,_
8589934291, 17179868809, 34359737299, 68719476391,_
137438953273, 274877906629, 549755813359, 1099511626399]]
Rep ==> Record(_
numOfEntries: Z,_
maxNumOfEntries: Z,_
numOfDeletedEntries: Z,_
maxNumOfVirtualEntries: Z,_
idx: Z,_
arr: Buckets,_
hashFunction: Key -> I,_
eqFunction: (Key,Key) -> Boolean)
localSearch(a: Buckets, k: Key, h: Key -> I, eq:(Key,Key) -> B): Z ==
update!(p, mk) ==>
p := p + h2
if p>=n then p := p-n
mk := getMKey(a, p)
n: Z := numOfBuckets a
h1: Z := (h k)::Z
p: Z := positiveRemainder(h1, n) -- position in array
h2: Z := 1 + positiveRemainder(h1, n-2)
mk: MKey := getMKey(a, p)
deletedPosition?: Boolean := false
while not vacant? mk repeat
deleted? mk => (deletedPosition? := true; break)
eq(k,toKey mk) => return p -- key found
update!(p, mk)
q := p -- first position of a free entry
-- We ignore DELETED entries when looking for the key.
while not vacant? mk repeat
not deleted? mk and eq(k,toKey mk) =>
setKeyEntry!(a, n, q, k, getEntry(a, n, p))
deleteKeyEntry!(a, n, p)
return q -- entry has been copied to previous DELETED position
update!(p, mk)
if deletedPosition? then q := q-n
q-n -- KEY not found.
newArr(n: N): Buckets == new(2*n, toUMKE VACANT)
rehashAux!(x: %, ix: Z): % ==
m: N := arrayLengths ix
r: Rep := rep x
h: Key -> I := r.hashFunction
eq: (Key,Key) -> B := r.eqFunction
a: Buckets := r.arr
n: Z := numOfBuckets a
c: Buckets := newArr m
for i in 0..n-1 | key?(mk: MKey := getMKey(a, i)) repeat
k: Key := toKey mk
-- Note that k is not in c, and there are no DELETED positions.
-- Thus, -m<=p<0.
p := m + localSearch(c, k, h, eq)
setKeyEntry!(c, m, p, k, getEntry(a, n, i))
r.arr := c --destructively set new array
r.idx := ix
r.maxNumOfEntries := maxLoad m
r.numOfDeletedEntries := 0
r.maxNumOfVirtualEntries := maxVirtualLoad m
x
grow!(x: %): % == rehashAux!(x, rep(x).idx + 1)
rehash!(x: %): % == rehashAux!(x, rep(x).idx)
table(hashfunction: Key -> SingleInteger,eqfunction: (Key,Key) -> Boolean): % ==
n: N := arrayLengths 0
maxEntries: Z := maxLoad n
maxVirtualEntries: Z := maxVirtualLoad n
hashfunction := forceLazySlot((hash$Key)@(Key -> I))$Lisp pretend (Key->I)
per [0, maxEntries, 0, maxVirtualEntries, 0, newArr n, hashfunction, eqfunction]
table(hashfunction: Key -> SingleInteger): % ==
table(hashfunction,forceLazySlot((_=$Key)@((Key,Key) -> B))$Lisp pretend ((Key,Key)->B))
empty(): % ==
table(forceLazySlot((hash$Key)@(Key -> I))$Lisp pretend (Key->I))
inspect(x: %): KE ==
a := rep(x).arr
n: Z := numOfBuckets a
for i in 0..n - 1 | key?(mk: MKey := getMKey(a, i)) repeat
return [toKey mk, getEntry(a, n, i)]
error "table must be non-empty"
#(x: %): N == rep(x).numOfEntries :: N
search(k: Key, x: %): Union(Entry, "failed") ==
a: Buckets := rep(x).arr
h: Key -> I := rep(x).hashFunction
eq: (Key,Key) -> B := rep(x).eqFunction
p: Z := localSearch(a, k, h, eq)
p<0 => "failed"
getEntry(a, numOfBuckets a, p)::UE
elt(x: %, k: Key): Entry ==
a: Buckets := rep(x).arr
h: Key -> I := rep(x).hashFunction
eq: (Key,Key) -> B := rep(x).eqFunction
p := localSearch(a, k, h, eq)
p<0 => error "key not in table"
getEntry(a, numOfBuckets a, p)
elt(x: %, k: Key, e: Entry): Entry ==
a: Buckets := rep(x).arr
h: Key -> I := rep(x).hashFunction
eq: (Key,Key) -> B := rep(x).eqFunction
p := localSearch(a, k, h, eq)
p<0 => e
getEntry(a, numOfBuckets a, p)
setelt!(x: %, k: Key, e: Entry): Entry ==
if rep(x).numOfEntries >= rep(x).maxNumOfEntries then grow! x
a: Buckets := rep(x).arr
h: Key -> I := rep(x).hashFunction
eq: (Key,Key) -> B := rep(x).eqFunction
p := localSearch(a, k, h, eq)
n: Z := numOfBuckets a
p>=0 => setEntry!(a, n, p, e)
r: Rep := rep x
r.numOfEntries := inc(r.numOfEntries)
p := n+p
p<0 => -- fill DELETED position
r.numOfDeletedEntries := dec(r.numOfDeletedEntries)
setKeyEntry!(a, n, n+p, k, e)
setKeyEntry!(a, n, p, k, e) -- fill VACANT position
if r.numOfEntries + r.numOfDeletedEntries > r.maxNumOfVirtualEntries then
rehash! x
e
remove!(k: Key, x: %): Union(Entry, "failed") ==
a: Buckets := rep(x).arr
h: Key -> I := rep(x).hashFunction
eq: (Key,Key) -> B := rep(x).eqFunction
p := localSearch(a, k, h, eq)
p<0 => "failed" -- key has not been found
n: Z := numOfBuckets a
e: Entry := getEntry(a, n, p) -- to be returned
deleteKeyEntry!(a, n, p)
rep(x).numOfEntries := dec(rep(x).numOfEntries)
rep(x).numOfDeletedEntries := inc(rep(x).numOfDeletedEntries)
e::UE
copy(x: %): % ==
r: Rep := rep x
per [r.numOfEntries, r.maxNumOfEntries,_
r.numOfDeletedEntries, r.maxNumOfVirtualEntries,_
r.idx, copy(r.arr), r.hashFunction, r.eqFunction]
fill!(x: %, e: Entry): % ==
a := rep(x).arr
n: N := numOfBuckets a
for i in 0..n-1 | key? getMKey(a, i) repeat setEntry!(a, n, i, e)
x
map!(f: Entry -> Entry, x: %): % ==
a := rep(x).arr
n: N := numOfBuckets a
for i in 0..n-1 | key? getMKey(a, i) repeat
setEntry!(a, n, i, f getEntry(a, n, i))
x
keys(x: %): List Key ==
a := rep(x).arr
l: List Key := empty()
for i in 0..numOfBuckets a - 1 | key?(mk: MKey := getMKey(a, i)) repeat
l := cons(toKey mk, l)
l
parts(x: %): List Entry ==
a := rep(x).arr
n: N := numOfBuckets a
l: List Entry := empty()
for i in 0..n-1 | key? getMKey(a, i) repeat
l := cons(getEntry(a, n, i), l)
l
parts(x: %): List KE ==
a := rep(x).arr
n: N := numOfBuckets a
l: List KE := empty()
for i in 0..n-1 | key?(mk: MKey := getMKey(a, i)) repeat
l := cons([toKey mk, getEntry(a, n, i)], l)
l
removeDuplicates(x: %): % == x
if Entry has BasicType then
((x: %) = (y: %)): Boolean ==
#x ~= #y => false
xa := rep(x).arr; xn := numOfBuckets xa
ya := rep(y).arr; yn := numOfBuckets ya
h := rep(y).hashFunction
eq := rep(y).eqFunction
for i in 0..xn - 1 | key?(mk: MKey := getMKey(xa, i)) repeat
p := localSearch(ya, toKey mk, h, eq)
p < 0 => return false
getEntry(xa, xn, i) ~= getEntry(ya, yn, p) => return false
true</spad>
fricas Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/8567553725698274317-25px001.spad
using old system compiler.
XHASHTBL abbreviates domain XHashTable
------------------------------------------------------------------------
initializing NRLIB XHASHTBL for XHashTable
compiling into NRLIB XHASHTBL
processing macro definition KE ==> Record(key: Key,entry: Entry)
processing macro definition UE ==> Union(Entry,failed)
processing macro definition Marker ==> None
processing macro definition toMarker mk ==> @(mk,None)
processing macro definition vacant? mk ==> (Sel Lisp EQ)(@(mk,None),VACANT)
processing macro definition deleted? mk ==> (Sel Lisp EQ)(@(mk,None),DELETED)
processing macro definition key? mk ==> SEQ(:=(G0: Boolean,(Sel Lisp EQ)(@(mk,None),VACANT)),exit(1,IF(G0,false,SEQ(:=(G1: Boolean,(Sel Lisp EQ)(@(mk,None),DELETED)),exit(1,IF(G1,false,true))))))
processing macro definition MKey ==> None
processing macro definition UMKE ==> None
processing macro definition Buckets ==> PrimitiveArray None
processing macro definition numOfBuckets a ==> shift(# a,- One)
processing macro definition toUMKE x ==> pretend(x,None)
processing macro definition toKey k ==> pretend(@(k,None),Key)
processing macro definition getMKey(a,i) ==> pretend(@(a i,None),None)
processing macro definition setKey!(a,i,k) ==> pretend(:=(a i,pretend(k,None)),Key)
processing macro definition getEntry(a,n,i) ==> pretend(a +(n,i),Entry)
processing macro definition setEntry!(a,n,i,e) ==> pretend(:=(a +(n,i),pretend(e,None)),Entry)
processing macro definition setKeyEntry!(a,n,i,k,e) ==> SEQ(pretend(:=(a i,pretend(k,None)),Key),exit(1,pretend(:=(a +(n,i),pretend(e,None)),Entry)))
processing macro definition deleteKeyEntry!(a,n,i) ==> SEQ(:=(a i,pretend(DELETED,None)),exit(1,:=(a +(n,i),pretend(VACANT,None))))
processing macro definition maxLoad n ==> quo(*(n,7),10)
processing macro definition maxVirtualLoad n ==> quo(*(n,9),10)
processing macro definition Rep ==> Record(numOfEntries: Integer,maxNumOfEntries: Integer,numOfDeletedEntries: Integer,maxNumOfVirtualEntries: Integer,idx: Integer,arr: PrimitiveArray None,hashFunction: Key -> SingleInteger,eqFunction: (Key,Key) -> Boolean)
compiling local localSearch : (PrimitiveArray None,Key,Key -> SingleInteger,(Key,Key) -> Boolean) -> Integer
processing macro definition update!(p,mk) ==> SEQ(:=(p,+(p,h2)),IF(>=(p,n),:=(p,-(p,n)),noBranch),exit(1,:=(mk,pretend(@(a p,None),None))))
Time: 0.03 SEC.
compiling local newArr : NonNegativeInteger -> PrimitiveArray None
Time: 0 SEC.
compiling local rehashAux! : (%,Integer) -> %
Time: 0.03 SEC.
compiling local grow! : % -> %
Time: 0 SEC.
compiling local rehash! : % -> %
Time: 0 SEC.
compiling exported table : (Key -> SingleInteger,(Key,Key) -> Boolean) -> %
****** comp fails at level 3 with expression: ******
error in function table
(@ (|Sel| |Key| |hash|) (|Mapping| (|SingleInteger|) |Key|))
****** level 3 ******
x:= ((Sel Key hash) G74)
m:= (SingleInteger)
f:=
((((#:G74 #) (#:G73 #) (#:G72 #) (|maxVirtualEntries| # #) ...)
((|rehash!| #) (|grow!| #)) ((|grow!| #) (|rehashAux!| #))
((|rehashAux!| #) (|newArr| #)) ...))
>> Apparent user error:
cannot compile ((Sel Key hash) G74)
|