Hall fricas (1) -> x := operator('x)
Type: BasicOperator?
fricas sif(n)==1/(subscript('x,
Type: Void
fricas sigma(n)==1/sif(n)^2*(sif(n+1)-2*sif(n)+sif(n-1)) Type: Void
fricas sigma(n) fricas Compiling function sif with type Variable(n) -> Fraction(Polynomial(
Integer))fricas Compiling function sif with type Polynomial(Integer) -> Fraction(
Polynomial(Integer))fricas Compiling function sigma with type Variable(n) -> Fraction(
Polynomial(Integer))
Type: Fraction(Polynomial(Integer))
fricas r(n)==1/4*(sigma(n+1)-sigma(n)) Type: Void
fricas numer r(n) fricas Compiling function sigma with type Polynomial(Integer) -> Fraction(
Polynomial(Integer))fricas Compiling function r with type Variable(n) -> Fraction(Polynomial(
Integer))
Type: Polynomial(Integer)
fricas factor denom(r(n))
Type: Factored(Polynomial(Integer))
Poirier to Hall1-D fricas C:List Symbol := [subscript('x,
Type: List(Symbol)
fricas d := #C
Type: PositiveInteger?
fricas J := matrix [[D(x(C(1),
Type: Matrix(Expression(Integer))
fricas K := inverse J
Type: Union(Matrix(Expression(Integer)),
fricas Req18a:=[reduce(+,
Type: List(Expression(Integer))
fricas diff1(n)==subscript('x,
Type: Void
fricas diff1(n) fricas Compiling function diff1 with type Variable(n) -> Polynomial(Integer
)
Type: Polynomial(Integer)
fricas Req18b:=eval(Req18a,
Type: List(Expression(Integer))
fricas diff2(n)==diff1(n)-diff1(n-1) Type: Void
fricas diff2(n) fricas Compiling function diff1 with type Polynomial(Integer) -> Polynomial
(Integer)fricas Compiling function diff2 with type Variable(n) -> Polynomial(Integer
)
Type: Polynomial(Integer)
fricas Req18c:=eval(Req18b, Type: List(Expression(Integer))
fricas numer Req18c.1
Type: SparseMultivariatePolynomial?(Integer,
fricas diff3(n)==diff2(n+1)-diff2(n) Type: Void
fricas diff3(n) fricas Compiling function diff2 with type Polynomial(Integer) -> Polynomial
(Integer)fricas Compiling function diff3 with type Variable(n) -> Polynomial(Integer
)
Type: Polynomial(Integer)
fricas Req18d:=eval(Req18c, Type: List(Expression(Integer))
fricas numer Req18d.1
Type: SparseMultivariatePolynomial?(Integer,
fricas diff4(n)==diff3(n+1)-diff3(n) Type: Void
fricas diff4(n) fricas Compiling function diff3 with type Polynomial(Integer) -> Polynomial
(Integer)fricas Compiling function diff4 with type Variable(n) -> Polynomial(Integer
)
Type: Polynomial(Integer)
fricas Req18e:=eval(Req18d, Type: List(Expression(Integer))
fricas --numer(Req18e.1-r(n)) factor numer Req18e.1
Type: Factored(SparseMultivariatePolynomial?(Integer,
fricas factor denom Req18e.1
Type: Factored(SparseMultivariatePolynomial?(Integer,
2-D fricas x := operator('x)
Type: BasicOperator?
fricas y := operator('y)
Type: BasicOperator?
fricas C:List Symbol := [subscript('x,
Type: List(Symbol)
fricas d := #C
Type: PositiveInteger?
fricas J := matrix [[D(x(C(1),
Type: Matrix(Expression(Integer))
fricas K := inverse J
Type: Union(Matrix(Expression(Integer)),
fricas Req18:=[reduce(+, Type: List(Expression(Integer))
fricas #Req18
Type: PositiveInteger?
fricas kernels Req18.1
Type: List(Kernel(Expression(Integer)))
|
|
|
|
last edited 10 years ago by Bill Page |
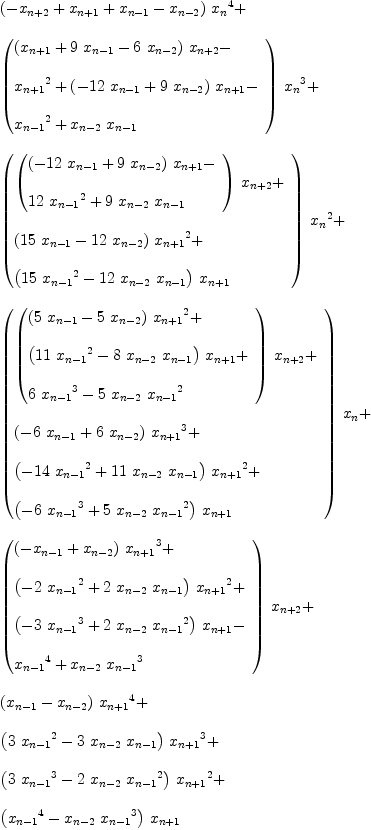
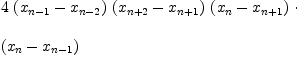
![\label{eq9}\left[ \frac{-{{{{x_{, 1}}\left({{x_{0}}, \: t}\right)}^{2}}\ {{x_{{{{, 1}{, 1}}{, 1}}{, 1}}}\left({{x_{0}}, \: t}\right)}}+{8 \ {{x_{, 1}}\left({{x_{0}}, \: t}\right)}\ {{x_{{, 1}{, 1}}}\left({{x_{0}}, \: t}\right)}\ {{x_{{{, 1}{, 1}}{, 1}}}\left({{x_{0}}, \: t}\right)}}-{{10}\ {{{x_{{, 1}{, 1}}}\left({{x_{0}}, \: t}\right)}^{3}}}}{4 \ {{{x_{, 1}}\left({{x_{0}}, \: t}\right)}^{6}}}\right]
\label{eq9}\left[ \frac{-{{{{x_{, 1}}\left({{x_{0}}, \: t}\right)}^{2}}\ {{x_{{{{, 1}{, 1}}{, 1}}{, 1}}}\left({{x_{0}}, \: t}\right)}}+{8 \ {{x_{, 1}}\left({{x_{0}}, \: t}\right)}\ {{x_{{, 1}{, 1}}}\left({{x_{0}}, \: t}\right)}\ {{x_{{{, 1}{, 1}}{, 1}}}\left({{x_{0}}, \: t}\right)}}-{{10}\ {{{x_{{, 1}{, 1}}}\left({{x_{0}}, \: t}\right)}^{3}}}}{4 \ {{{x_{, 1}}\left({{x_{0}}, \: t}\right)}^{6}}}\right]](images/3102873228799416215-16.0px.png)
![\label{eq11}\left[ \frac{{{\left(-{{x_{n}}^{2}}+{2 \ {x_{n - 1}}\ {x_{n}}}-{{x_{n - 1}}^{2}}\right)}\ {{x_{{{{, 1}{, 1}}{, 1}}{, 1}}}\left({{x_{0}}, \: t}\right)}}+{{\left({8 \ {x_{n}}}-{8 \ {x_{n - 1}}}\right)}\ {{x_{{, 1}{, 1}}}\left({{x_{0}}, \: t}\right)}\ {{x_{{{, 1}{, 1}}{, 1}}}\left({{x_{0}}, \: t}\right)}}-{{10}\ {{{x_{{, 1}{, 1}}}\left({{x_{0}}, \: t}\right)}^{3}}}}{{4 \ {{x_{n}}^{6}}}-{{24}\ {x_{n - 1}}\ {{x_{n}}^{5}}}+{{60}\ {{x_{n - 1}}^{2}}\ {{x_{n}}^{4}}}-{{80}\ {{x_{n - 1}}^{3}}\ {{x_{n}}^{3}}}+{{60}\ {{x_{n - 1}}^{4}}\ {{x_{n}}^{2}}}-{{24}\ {{x_{n - 1}}^{5}}\ {x_{n}}}+{4 \ {{x_{n - 1}}^{6}}}}\right]
\label{eq11}\left[ \frac{{{\left(-{{x_{n}}^{2}}+{2 \ {x_{n - 1}}\ {x_{n}}}-{{x_{n - 1}}^{2}}\right)}\ {{x_{{{{, 1}{, 1}}{, 1}}{, 1}}}\left({{x_{0}}, \: t}\right)}}+{{\left({8 \ {x_{n}}}-{8 \ {x_{n - 1}}}\right)}\ {{x_{{, 1}{, 1}}}\left({{x_{0}}, \: t}\right)}\ {{x_{{{, 1}{, 1}}{, 1}}}\left({{x_{0}}, \: t}\right)}}-{{10}\ {{{x_{{, 1}{, 1}}}\left({{x_{0}}, \: t}\right)}^{3}}}}{{4 \ {{x_{n}}^{6}}}-{{24}\ {x_{n - 1}}\ {{x_{n}}^{5}}}+{{60}\ {{x_{n - 1}}^{2}}\ {{x_{n}}^{4}}}-{{80}\ {{x_{n - 1}}^{3}}\ {{x_{n}}^{3}}}+{{60}\ {{x_{n - 1}}^{4}}\ {{x_{n}}^{2}}}-{{24}\ {{x_{n - 1}}^{5}}\ {x_{n}}}+{4 \ {{x_{n - 1}}^{6}}}}\right]](images/7061858964195614565-16.0px.png)
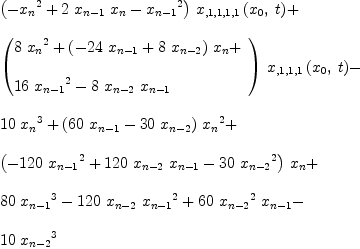
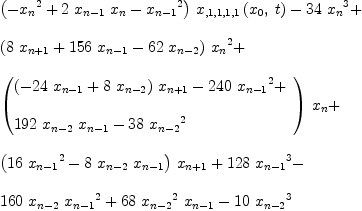
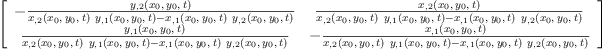
![\label{eq26}\begin{array}{@{}l}
\displaystyle
\left[{{y_{{{{, 1}{, 1}}{, 1}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{{{, 1}{, 1}}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{{{, 1}{, 2}}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{y_{{{{, 1}{, 1}}{, 1}}{, 1}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{{{, 2}{, 2}}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{{{, 1}{, 1}}{, 1}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{x_{{{{, 1}{, 1}}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{{{, 1}{, 2}}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{{{, 1}{, 1}}{, 1}}{, 1}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{x_{{{{, 2}{, 2}}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{{, 1}{, 1}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{{, 1}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{y_{{{, 1}{, 1}}{, 1}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{{, 2}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{{, 1}{, 1}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{x_{{{, 1}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{{, 1}{, 1}}{, 1}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{{, 2}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{y_{{, 1}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{, 1}{, 1}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{, 2}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{x_{{, 1}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{, 1}{, 1}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{, 2}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{y_{, 1}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{, 2}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{, 1}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{, 2}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}\right]
\label{eq26}\begin{array}{@{}l}
\displaystyle
\left[{{y_{{{{, 1}{, 1}}{, 1}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{{{, 1}{, 1}}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{{{, 1}{, 2}}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{y_{{{{, 1}{, 1}}{, 1}}{, 1}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{{{, 2}{, 2}}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{{{, 1}{, 1}}{, 1}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{x_{{{{, 1}{, 1}}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{{{, 1}{, 2}}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{{{, 1}{, 1}}{, 1}}{, 1}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{x_{{{{, 2}{, 2}}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{{, 1}{, 1}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{{, 1}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{y_{{{, 1}{, 1}}{, 1}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{{, 2}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{{, 1}{, 1}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{x_{{{, 1}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{{, 1}{, 1}}{, 1}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{{, 2}{, 2}}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{y_{{, 1}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{, 1}{, 1}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{{, 2}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{x_{{, 1}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{, 1}{, 1}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{{, 2}{, 2}}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \: \right.
\
\
\displaystyle
\left.{{y_{, 1}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{y_{, 2}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{, 1}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}, \:{{x_{, 2}}\left({{x_{0}}, \:{y_{0}}, \: t}\right)}\right]](images/1965526680063494938-16.0px.png)