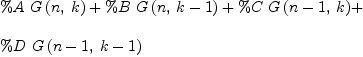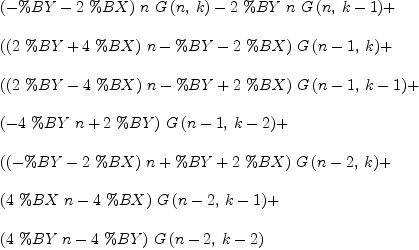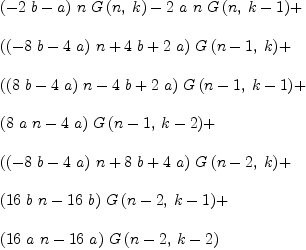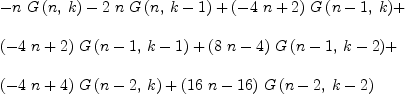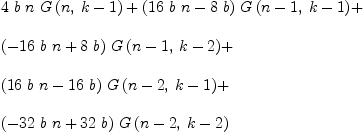fricas
(1) -> <spad>
fricas
)abbrev package SUMMPACK SummPack
SummPack(): Exports == Implementation where
FPI ==> Fraction Polynomial Integer
X ==> Expression Integer
NNI ==> NonNegativeInteger
PI ==> PositiveInteger
POLINT ==> Polynomial Integer
BOP ==> BasicOperator
Exports == with
coeffMatrix : (PI,PI) -> Matrix X
funcMatrix : ((X,X)->X,PI,PI) -> Matrix X
sumAndNormalize : (Matrix X,Matrix X) -> X
retractNumeratorToPolyInt : X -> Polynomial Integer
findCoeffs : (POLINT,Matrix X, Symbol) -> List Equation FPI
formalExpr : (BOP,Matrix X,PI,PI) -> X
celine : ((X,X)->X,PI,PI) -> X
celine2 : ((X,X)->X,BOP,PI,PI) -> X
Implementation == add
coeffMatrix(I:PI,J:PI):Matrix X ==
matrix [[new()$Symbol::X for i in 0..I] for j in 0..J]
funcMatrix(F:(X,X)->X,I:PI,J:PI):Matrix X ==
n:X:='n::X
k:X:='k::X
matrix [[F(n-j::X,k-i::X)/F(n,k) for i in 0..I] for j in 0..J]
sumAndNormalize(CM:Matrix X, FM:Matrix X):X ==
n:=nrows(CM)
t:X:=trace(squareMatrix(CM*transpose(FM))$SquareMatrix(n,X))
normalize(t)$ElementaryFunctionStructurePackage(Integer,X)
retractNumeratorToPolyInt(san:X):Polynomial Integer ==
p:Polynomial Integer:=retract(numerator san)
return p
findCoeffs(p:POLINT,m:Matrix X,k:Symbol):List Equation FPI ==
d:=degree(p,k)
eqs:List Equation FPI:=[coefficient(p,k,l)::FPI=0 for l in 0..d]
v:=members m
x:=variables v
sol:=solve(eqs,x)$SystemSolvePackage(Integer) --$TransSolvePackage(Integer)
first sol
convToFPI(M:Matrix X):Matrix FPI ==
m:=copy(M)
nr:=nrows(m)
nc:=ncols(m)
r:=zero(nr,nc)$Matrix(FPI)
for i in 1..nr repeat
for j in 1..nc repeat
r(i,j):=retract m(i,j)
return r
formalExpr(op:BOP,cm:Matrix X,I:PI,J:PI):X ==
d:=nrows(cm)
n:X:='n::X
k:X:='k::X
g:Matrix(X):=matrix [[op(n-j::X,k-i::X) for i in 0..I] for j in 0..J]
t:X:=trace(squareMatrix(cm*transpose(g))$SquareMatrix(d,X))
return t
celine(F:(X,X)->X,I:PI,J:PI):X ==
cm:Matrix X:=coeffMatrix(I,J)
fm:=funcMatrix(F,I,J)
san:=sumAndNormalize(cm,fm)
p:=retractNumeratorToPolyInt(san)
--
seq:=findCoeffs(p,cm,'k)
e:List Equation X:=[lhs(x)::X=rhs(x)::X for x in seq]
G:=operator 'G
fex:X:=formalExpr(G,cm,I,J)
subst(fex,e)
celine2(F:(X,X)->X,op:BOP,I:PI,J:PI):X ==
cm:Matrix X:=coeffMatrix(I,J)
fm:=funcMatrix(F,I,J)
san:=sumAndNormalize(cm,fm)
p:=retractNumeratorToPolyInt(san)
--
seq:=findCoeffs(p,cm,'k)
e:List Equation X:=[lhs(x)::X=rhs(x)::X for x in seq]
fex:X:=formalExpr(op,cm,I,J)
subst(fex,e)
-- C:=celine2((k,n)+->binomial(n,k),operator 'T,1,1)
-- variables(%)
-- C=0 ; %/?%
-- sum(C,k=1..n), tower(C), kernels(C), variables C, mainKernel C</spad>
fricas
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/4749327676615086707-25px001.spad
using old system compiler.
SUMMPACK abbreviates package SummPack
------------------------------------------------------------------------
initializing NRLIB SUMMPACK for SummPack
compiling into NRLIB SUMMPACK
compiling exported coeffMatrix : (PositiveInteger,PositiveInteger) -> Matrix Expression Integer
Time: 0.04 SEC.
compiling exported funcMatrix : ((Expression Integer,Expression Integer) -> Expression Integer,PositiveInteger,PositiveInteger) -> Matrix Expression Integer
Time: 0.01 SEC.
compiling exported sumAndNormalize : (Matrix Expression Integer,Matrix Expression Integer) -> Expression Integer
Time: 0.02 SEC.
compiling exported retractNumeratorToPolyInt : Expression Integer -> Polynomial Integer
Time: 0 SEC.
compiling exported findCoeffs : (Polynomial Integer,Matrix Expression Integer,Symbol) -> List Equation Fraction Polynomial Integer
Time: 0.01 SEC.
compiling local convToFPI : Matrix Expression Integer -> Matrix Fraction Polynomial Integer
Time: 0 SEC.
compiling exported formalExpr : (BasicOperator,Matrix Expression Integer,PositiveInteger,PositiveInteger) -> Expression Integer
Time: 0.02 SEC.
compiling exported celine : ((Expression Integer,Expression Integer) -> Expression Integer,PositiveInteger,PositiveInteger) -> Expression Integer
Time: 0 SEC.
compiling exported celine2 : ((Expression Integer,Expression Integer) -> Expression Integer,BasicOperator,PositiveInteger,PositiveInteger) -> Expression Integer
Time: 0 SEC.
(time taken in buildFunctor: 0)
;;; *** |SummPack| REDEFINED
;;; *** |SummPack| REDEFINED
Time: 0 SEC.
Warnings:
[1] sumAndNormalize: not known that (AlgebraicallyClosedField) is of mode (CATEGORY domain (IF (has (Integer) (IntegralDomain)) (PROGN (ATTRIBUTE (AlgebraicallyClosedFunctionSpace (Integer))) (ATTRIBUTE (TranscendentalFunctionCategory)) (ATTRIBUTE (CombinatorialOpsCategory)) (ATTRIBUTE (LiouvillianFunctionCategory)) (ATTRIBUTE (SpecialFunctionCategory)) (SIGNATURE reduce (% %)) (SIGNATURE number? ((Boolean) %)) (IF (has (Integer) (PolynomialFactorizationExplicit)) (ATTRIBUTE (PolynomialFactorizationExplicit)) noBranch) (SIGNATURE setSimplifyDenomsFlag ((Boolean) (Boolean))) (SIGNATURE getSimplifyDenomsFlag ((Boolean)))) noBranch))
[2] sumAndNormalize: not known that (TranscendentalFunctionCategory) is of mode (CATEGORY domain (IF (has (Integer) (IntegralDomain)) (PROGN (ATTRIBUTE (AlgebraicallyClosedFunctionSpace (Integer))) (ATTRIBUTE (TranscendentalFunctionCategory)) (ATTRIBUTE (CombinatorialOpsCategory)) (ATTRIBUTE (LiouvillianFunctionCategory)) (ATTRIBUTE (SpecialFunctionCategory)) (SIGNATURE reduce (% %)) (SIGNATURE number? ((Boolean) %)) (IF (has (Integer) (PolynomialFactorizationExplicit)) (ATTRIBUTE (PolynomialFactorizationExplicit)) noBranch) (SIGNATURE setSimplifyDenomsFlag ((Boolean) (Boolean))) (SIGNATURE getSimplifyDenomsFlag ((Boolean)))) noBranch))
Cumulative Statistics for Constructor SummPack
Time: 0.13 seconds
finalizing NRLIB SUMMPACK
Processing SummPack for Browser database:
--->-->SummPack(constructor): Not documented!!!!
--->-->SummPack((coeffMatrix ((Matrix (Expression (Integer))) (PositiveInteger) (PositiveInteger)))): Not documented!!!!
--->-->SummPack((funcMatrix ((Matrix (Expression (Integer))) (Mapping (Expression (Integer)) (Expression (Integer)) (Expression (Integer))) (PositiveInteger) (PositiveInteger)))): Not documented!!!!
--->-->SummPack((sumAndNormalize ((Expression (Integer)) (Matrix (Expression (Integer))) (Matrix (Expression (Integer)))))): Not documented!!!!
--->-->SummPack((retractNumeratorToPolyInt ((Polynomial (Integer)) (Expression (Integer))))): Not documented!!!!
--->-->SummPack((findCoeffs ((List (Equation (Fraction (Polynomial (Integer))))) (Polynomial (Integer)) (Matrix (Expression (Integer))) (Symbol)))): Not documented!!!!
--->-->SummPack((formalExpr ((Expression (Integer)) (BasicOperator) (Matrix (Expression (Integer))) (PositiveInteger) (PositiveInteger)))): Not documented!!!!
--->-->SummPack((celine ((Expression (Integer)) (Mapping (Expression (Integer)) (Expression (Integer)) (Expression (Integer))) (PositiveInteger) (PositiveInteger)))): Not documented!!!!
--->-->SummPack((celine2 ((Expression (Integer)) (Mapping (Expression (Integer)) (Expression (Integer)) (Expression (Integer))) (BasicOperator) (PositiveInteger) (PositiveInteger)))): Not documented!!!!
--->-->SummPack(): Missing Description
; compiling file "/var/aw/var/LatexWiki/SUMMPACK.NRLIB/SUMMPACK.lsp" (written 15 MAR 2025 09:47:05 AM):
; wrote /var/aw/var/LatexWiki/SUMMPACK.NRLIB/SUMMPACK.fasl
; compilation finished in 0:00:00.036
------------------------------------------------------------------------
SummPack is now explicitly exposed in frame initial
SummPack will be automatically loaded when needed from
/var/aw/var/LatexWiki/SUMMPACK.NRLIB/SUMMPACKTest different flavours
fricas
--)co sumpack
X==>EXPR INT
Type: Void
fricas
F:=(n:X,k:X):X+->k*binomial(n,k)
Type: ((Expression(Integer), Expression(Integer)) -> Expression(Integer))
fricas
cm:=coeffMatrix(1,1)
Type: Matrix(Expression(Integer))
fricas
fm:=funcMatrix(F,1,1)
Type: Matrix(Expression(Integer))
fricas
san:=sumAndNormalize(cm,fm)
Type: Expression(Integer)
fricas
p:=retractNumeratorToPolyInt(san)
Type: Polynomial(Integer)
fricas
--
d:=degree(p,k)
fricas
eqs:=[coefficient(p,k,l)=0 for l in 0..d]
Type: List(Equation(Polynomial(Integer)))
fricas
v:=members cm
Type: List(Expression(Integer))
fricas
vv:=variables(v)
Type: List(Symbol)
fricas
x:=[s::Symbol for s in v]
Type: List(Symbol)
fricas
sol:=solve(eqs,x) -- check #sol=1
Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas
e:=findCoeffs(p,cm,k)
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
ss:=eval(cm,sol.1)
Type: Matrix(Expression(Integer))
fricas
--
G:=operator 'G
fricas
I:=J:=1
fricas
g:Matrix(X):=matrix [[G(n-j,k-i) for i in 0..I] for j in 0..J]
Type: Matrix(Expression(Integer))
fricas
sf:Matrix X:=ss*transpose(g)
Type: Matrix(Expression(Integer))
fricas
res:X:=reduce(_+,[sf(i,i) for i in 1..I+1])
Type: Expression(Integer)
fricas
fex:=formalExpr(G,cm,I,J)
Type: Expression(Integer)
fricas
H:=(n:X,k:X):X+->binomial(n,k)
Type: ((Expression(Integer), Expression(Integer)) -> Expression(Integer))
fricas
celine(H,1,1)
Type: Expression(Integer)
fricas
Q:=(n:X,k:X):X+->binomial(n,k)^2
Type: ((Expression(Integer), Expression(Integer)) -> Expression(Integer))
fricas
celine(Q,2,2)
Type: Expression(Integer)
fricas
R:=(n:X,k:X):X+->(-1)^k*factorial(n)*'x::X^k/(factorial(k)^2*factorial(n-k))
Type: ((Expression(Integer), Expression(Integer)) -> Expression(Integer))
fricas
RC:=celine(R,2,2)
Type: Expression(Integer)
fricas
ch:=n*R(n,k-1)+(-2*n+1)*R(n-1,k-1)+'x::X*R(n-1,k-2)+(n-1)*R(n-2,k-1)
Type: Expression(Integer)
fricas
normalize(ch)
Type: Expression(Integer)
fricas
celine((n,k)+->n*k,1,1)
Type: Expression(Integer)
fricas
-- [13] (D,List(Equation(D2))) -> D from D
-- if D has EVALAB(D2) and D2 has SETCAT
-- [32] (Fraction(Polynomial(D3)),List(Equation(Fraction(Polynomial(D3)
-- )))) -> Fraction(Polynomial(D3))
-- from RationalFunction(D3) if D3 has INTDOM
SC:=celine((n,k)+->binomial(n,k)*binomial(2*k,k)*(-1/2)^k,2,2)
Type: Expression(Integer)
fricas
SCA:=subst(SC,[%DA=a,%CZ=b])*4*(n-1)
Type: Expression(Integer)
fricas
--
SC2:=celine((n,k)+->binomial(n,k)*binomial(2*k,k)*(-2)^(n-k),2,2)
Type: Expression(Integer)
fricas
SCA2:=subst(SC2,[%CJ=a,%CI=b])*16*(n-1)
Type: Expression(Integer)
fricas
SCB2:=subst(SCA2,[a=1,b=0])
Type: Expression(Integer)
fricas
-- Example 4.3.3 of A=B (subst to get same result)
SCB3:=subst(SCA2,[a=-2*b])
Type: Expression(Integer)
fricas
SCB3:=subst(%,[b=1/4])
Type: Expression(Integer)
fricas
SCB3:=subst(%,[k=k+1])
Type: Expression(Integer)
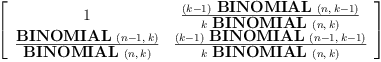

![\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[{{{{\left(\%C + \%A \right)}\ {{n}^{2}}}+{{\left(- \%D + \%C - \%B + \%A \right)}\ n}- \%D}= 0}, \: \right.
\
\
\displaystyle
\left.{{{{\left(\%D -{2 \ \%C}+ \%B - \%A \right)}\ n}+{2 \ \%D}- \%C}= 0}, \: \right.
\
\
\displaystyle
\left.{{- \%D + \%C}= 0}\right]
\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[{{{{\left(\%C + \%A \right)}\ {{n}^{2}}}+{{\left(- \%D + \%C - \%B + \%A \right)}\ n}- \%D}= 0}, \: \right.
\
\
\displaystyle
\left.{{{{\left(\%D -{2 \ \%C}+ \%B - \%A \right)}\ n}+{2 \ \%D}- \%C}= 0}, \: \right.
\
\
\displaystyle
\left.{{- \%D + \%C}= 0}\right]](images/7355732315081577311-16.0px.png)