|
|
|
last edited 5 years ago by test1 |
Edit detail for SandBoxVeryLongLaTeX revision 1 of 5
| 1 2 3 4 5 | ||
|
Editor: page
Time: 2007/11/26 19:30:35 GMT-8 |
||
| Note: transferred from axiom-developer | ||
changed: - Examples of Axiom output that causes problems for the LineBreaker program: The Robert Sutor LineBreaker program is embedded in the LaTeX handling programs for this web site. It has also been used experimentally in the TeXmacs - Axiom interface program called tm_axiom. There have been problems reported concerning incorrect formatting that may be due to problems with the LineBreaker programs. Examples of such problems are collected below. Experiment 0 The first example below was reported by Andrey G. Grozin as failing when displayed in TeXmacs when using the Sutor line-break algorithm. But typeset and folded correctly by TeXmacs without the line-break algorithm. However it does appear correctly below and it is also correct in the most recent versions of TeXmacs (1.0.4.5 on cygwin and 1.0.4.4 on native windows) when using the newest version of "tm_axiom":http://page.axiom-developer.org/tm_axiom.zip and the version of Axiom at AxiomBinaries. \begin{axiom} (x+y+z)^10 \end{axiom} Experiment 1 This expression is not folded at all by the current version of TeXmacs but it displayed correctly both here and in TeXmacs when using the line-break algorithm. \begin{axiom} (1/x+y+z)^10 \end{axiom} Experiment 2 This is the first example in the Jenks and Sutor AXIOM book. It is formatted properly below but in TeXmacs the output is wrong - small instead of large brackets and one of the terms of the numerator not display at all. Without the line-break algorithm TeXmacs displays it correctly but as one long non- folded line. \begin{axiom} integrate (1/(x**3 * (a+b*x)**(1/3)),x) \end{axiom} Experiment 3 This simple variant of the above expression, (-1/3) instead of (1/3), is formatted properly both here and in TeXmacs \begin{axiom} integrate (1/(x**3 * (a+b*x)**(-1/3)),x) \end{axiom} Notice that the first term in the paranthesis appears a little odd at first site because the first term itself is "locally folded" at the ${\mathbf \cdot}$ with a vertically centered leading minus sign.
Examples of Axiom output that causes problems for the LineBreaker? program:
The Robert Sutor LineBreaker? program is embedded in the LaTeX? handling programs for this web site. It has also been used experimentally in the TeXmacs? - Axiom interface program called tm_axiom.
There have been problems reported concerning incorrect formatting that may be due to problems with the LineBreaker? programs. Examples of such problems are collected below.
Experiment 0
The first example below was reported by Andrey G. Grozin as failing when displayed in TeXmacs? when using the Sutor line-break algorithm. But typeset and folded correctly by TeXmacs? without the line-break algorithm. However it does appear correctly below and it is also correct in the most recent versions of TeXmacs? (1.0.4.5 on cygwin and 1.0.4.4 on native windows) when using the newest version of tm_axiom and the version of Axiom at AxiomBinaries?.
(x+y+z)^10
![\label{eq1}\begin{array}{@{}l}
\displaystyle
{z^{10}}+{{\left({{10}\ y}+{{10}\ x}\right)}\ {z^9}}+{{\left({{4
5}\ {y^2}}+{{90}\ x \ y}+{{45}\ {x^2}}\right)}\ {z^8}}+
\
\
\displaystyle
{{\left({{120}\ {y^3}}+{{360}\ x \ {y^2}}+{{360}\ {x^2}\ y}+{{120}\ {x^3}}\right)}\ {z^7}}+
\
\
\displaystyle
{{\left({{210}\ {y^4}}+{{840}\ x \ {y^3}}+{{1260}\ {x^2}\ {y^2}}+{{840}\ {x^3}\ y}+{{210}\ {x^4}}\right)}\ {z^6}}+
\
\
\displaystyle
{{\left({
\begin{array}{@{}l}
\displaystyle
{{252}\ {y^5}}+{{1260}\ x \ {y^4}}+{{2520}\ {x^2}\ {y^3}}+{{2
520}\ {x^3}\ {y^2}}+
\
\
\displaystyle
{{1260}\ {x^4}\ y}+{{252}\ {x^5}}](images/6355180578132784421-16.0px.png "\label{eq1}\begin{array}{@{}l}
\displaystyle
{z^{10}}+{{\left({{10}\ y}+{{10}\ x}\right)}\ {z^9}}+{{\left({{4
5}\ {y^2}}+{{90}\ x \ y}+{{45}\ {x^2}}\right)}\ {z^8}}+
\
\
\displaystyle
{{\left({{120}\ {y^3}}+{{360}\ x \ {y^2}}+{{360}\ {x^2}\ y}+{{120}\ {x^3}}\right)}\ {z^7}}+
\
\
\displaystyle
{{\left({{210}\ {y^4}}+{{840}\ x \ {y^3}}+{{1260}\ {x^2}\ {y^2}}+{{840}\ {x^3}\ y}+{{210}\ {x^4}}\right)}\ {z^6}}+
\
\
\displaystyle
{{\left({
\begin{array}{@{}l}
\displaystyle
{{252}\ {y^5}}+{{1260}\ x \ {y^4}}+{{2520}\ {x^2}\ {y^3}}+{{2
520}\ {x^3}\ {y^2}}+
\
\
\displaystyle
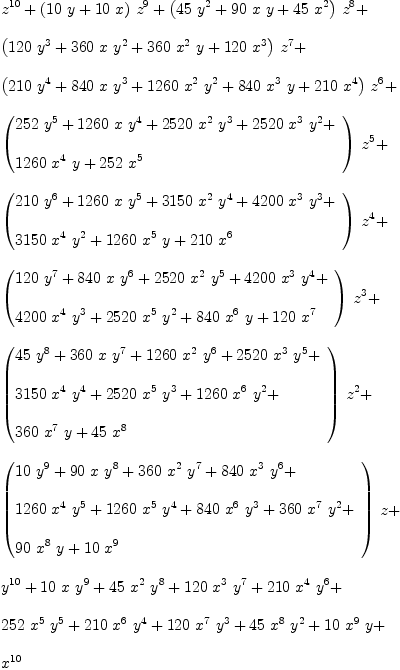{{1260}\ {x^4}\ y}+{{252}\ {x^5}}") | (1) |
Experiment 1
This expression is not folded at all by the current version of TeXmacs? but it displayed correctly both here and in TeXmacs? when using the line-break algorithm.
(1/x+y+z)^10
![\label{eq2}{\left(
\begin{array}{@{}l}
\displaystyle
{{x^{10}}\ {z^{10}}}+{{\left({{10}\ {x^{10}}\ y}+{{10}\ {x^9}}\right)}\ {z^9}}+
\
\
\displaystyle
{{\left({{45}\ {x^{10}}\ {y^2}}+{{90}\ {x^9}\ y}+{{45}\ {x^8}}\right)}\ {z^8}}+
\
\
\displaystyle
{{\left({{120}\ {x^{10}}\ {y^3}}+{{360}\ {x^9}\ {y^2}}+{{360}\ {x^8}\ y}+{{120}\ {x^7}}\right)}\ {z^7}}+
\
\
\displaystyle
{{\left({
\begin{array}{@{}l}
\displaystyle
{{210}\ {x^{10}}\ {y^4}}+{{840}\ {x^9}\ {y^3}}+{{1260}\ {x^8}\ {y^2}}+
\
\
\displaystyle
{{840}\ {x^7}\ y}+{{210}\ {x^6}}](images/1401979331169129662-16.0px.png "\label{eq2}{\left(
\begin{array}{@{}l}
\displaystyle
{{x^{10}}\ {z^{10}}}+{{\left({{10}\ {x^{10}}\ y}+{{10}\ {x^9}}\right)}\ {z^9}}+
\
\
\displaystyle
{{\left({{45}\ {x^{10}}\ {y^2}}+{{90}\ {x^9}\ y}+{{45}\ {x^8}}\right)}\ {z^8}}+
\
\
\displaystyle
{{\left({{120}\ {x^{10}}\ {y^3}}+{{360}\ {x^9}\ {y^2}}+{{360}\ {x^8}\ y}+{{120}\ {x^7}}\right)}\ {z^7}}+
\
\
\displaystyle
{{\left({
\begin{array}{@{}l}
\displaystyle
{{210}\ {x^{10}}\ {y^4}}+{{840}\ {x^9}\ {y^3}}+{{1260}\ {x^8}\ {y^2}}+
\
\
\displaystyle
{{840}\ {x^7}\ y}+{{210}\ {x^6}}") | (2) |
Experiment 2
This is the first example in the Jenks and Sutor AXIOM book. It is formatted properly below but in TeXmacs? the output is wrong - small instead of large brackets and one of the terms of the numerator not display at all. Without the line-break algorithm TeXmacs? displays it correctly but as one long non- folded line.
integrate (1/(x**3 * (a+b*x)**(1/3)),x)
![\label{eq3}{\left(
\begin{array}{@{}l}
\displaystyle
-
\
\
\displaystyle
{2 \ {b^2}\ {x^2}\ {\sqrt{3}}\ {\log \left({{{\root{3}\of{a}}\ {{\root{3}\of{{b \ x}+ a}}^2}}+{{{\root{3}\of{a}}^2}\ {\root{3}\of{{b \ x}+ a}}}+ a}\right)}}+
\
\
\displaystyle
{4 \ {b^2}\ {x^2}\ {\sqrt{3}}\ {\log \left({{{{\root{3}\of{a}}^2}\ {\root{3}\of{{b \ x}+ a}}}- a}\right)}}+
\
\
\displaystyle
{{12}\ {b^2}\ {x^2}\ {\arctan \left({{{2 \ {\sqrt{3}}\ {{\root{3}\of{a}}^2}\ {\root{3}\of{{b \ x}+ a}}}+{a \ {\sqrt{3}}}}\over{3 \ a}}\right)}}+
\
\
\displaystyle
{{\left({{12}\ b \ x}-{9 \ a}\right)}\ {\sqrt{3}}\ {\root{3}\of{a}}\ {{\root{3}\of{{b \ x}+ a}}^2}}](images/4949879071348506728-16.0px.png "\label{eq3}{\left(
\begin{array}{@{}l}
\displaystyle
-
\
\
\displaystyle
{2 \ {b^2}\ {x^2}\ {\sqrt{3}}\ {\log \left({{{\root{3}\of{a}}\ {{\root{3}\of{{b \ x}+ a}}^2}}+{{{\root{3}\of{a}}^2}\ {\root{3}\of{{b \ x}+ a}}}+ a}\right)}}+
\
\
\displaystyle
{4 \ {b^2}\ {x^2}\ {\sqrt{3}}\ {\log \left({{{{\root{3}\of{a}}^2}\ {\root{3}\of{{b \ x}+ a}}}- a}\right)}}+
\
\
\displaystyle
{{12}\ {b^2}\ {x^2}\ {\arctan \left({{{2 \ {\sqrt{3}}\ {{\root{3}\of{a}}^2}\ {\root{3}\of{{b \ x}+ a}}}+{a \ {\sqrt{3}}}}\over{3 \ a}}\right)}}+
\
\
\displaystyle
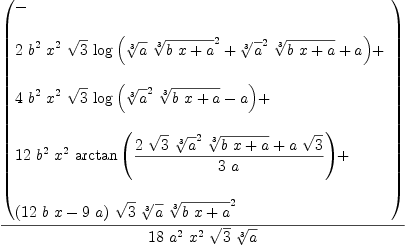{{\left({{12}\ b \ x}-{9 \ a}\right)}\ {\sqrt{3}}\ {\root{3}\of{a}}\ {{\root{3}\of{{b \ x}+ a}}^2}}") | (3) |
Experiment 3
This simple variant of the above expression, (-1/3) instead of (1/3), is formatted properly both here and in TeXmacs?
integrate (1/(x**3 * (a+b*x)**(-1/3)),x)
![\label{eq4}{\left(
\begin{array}{@{}l}
\displaystyle
-{
\begin{array}{@{}l}
\displaystyle
{b^2}\ {x^2}\ {\sqrt{3}}\ \cdot
\
\
\displaystyle
{\log{{\left({{{{\root{3}\of{-{a^2}}}^2}\ {{\root{3}\of{{b \ x}+ a}}^2}}-{a \ {\root{3}\of{-{a^2}}}\ {\root{3}\of{{b \ x}+ a}}}+{a^2}}\right)}}}](images/538324918736580619-16.0px.png "\label{eq4}{\left(
\begin{array}{@{}l}
\displaystyle
-{
\begin{array}{@{}l}
\displaystyle
{b^2}\ {x^2}\ {\sqrt{3}}\ \cdot
\
\
\displaystyle
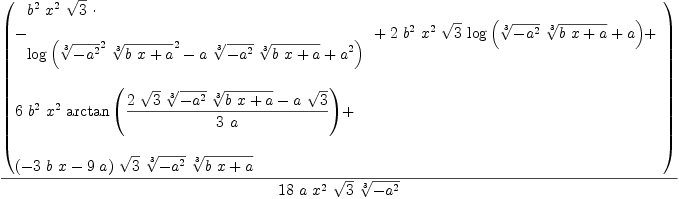{\log{{\left({{{{\root{3}\of{-{a^2}}}^2}\ {{\root{3}\of{{b \ x}+ a}}^2}}-{a \ {\root{3}\of{-{a^2}}}\ {\root{3}\of{{b \ x}+ a}}}+{a^2}}\right)}}}") | (4) |
Notice that the first term in the paranthesis appears a little
odd at first site because the first term itself is "locally
folded" at the 
with a vertically centered leading minus sign.