Refs:
We need the Axiom LinearOperator library.
fricas
(1) -> )library CARTEN ARITY CMONAL CPROP CLOP CALEY
>> System error:
The value
15684
is not of type
LIST
Use the following macros for convenient notation
fricas
-- summation
macro Σ(x,i,n)==reduce(+,[x for i in n])
Type: Void
fricas
-- list
macro Ξ(f,i,n)==[f for i in n]
Type: Void
fricas
-- subscript and superscripts
macro sb == subscript
Type: Void
fricas
macro sp == superscript
Type: Void
𝐋 is the domain of 2-dimensional linear operators over the rational functions ℚ (Expression Integer), i.e. ratio of polynomials with integer coefficients.
fricas
dim:=2
fricas
macro ℒ == List
Type: Void
fricas
macro ℂ == CaleyDickson
Type: Void
fricas
macro ℚ == Expression Integer
Type: Void
fricas
𝐋 := ClosedLinearOperator(OVAR ['1,'2], ℚ)
There are no library operations named ClosedLinearOperator
Use HyperDoc Browse or issue
)what op ClosedLinearOperator
to learn if there is any operation containing "
ClosedLinearOperator " in its name.
Cannot find a definition or applicable library operation named
ClosedLinearOperator with argument type(s)
Type
Type
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
We want to be able to implement linear operators with two
"colors" like the following:
An example starting with Complex Algebra
The basis consists of the real and imaginary units. We use complex multiplication to form the "multiplication table" as a matrix. Then the structure constants can be obtained by dividing each matrix entry by the list of basis vectors.
Split-complex can be specified by Caley-Dickson parameter (q0 = -1)
fricas
--q:=1 -- split-complex
q:=sp('i,[2])
Type: Symbol
fricas
QQ := ℂ(ℚ,'i,q);
There are no library operations named CaleyDickson
Use HyperDoc Browse or issue
)what op CaleyDickson
to learn if there is any operation containing " CaleyDickson " in
its name.
Cannot find a definition or applicable library operation named
CaleyDickson with argument type(s)
Type
Variable(i)
Symbol
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
Basis: Each B.i is a complex number
fricas
B:ℒ QQ := map(x +-> hyper x,1$SQMATRIX(dim,ℚ)::ℒ ℒ ℚ)
QQ is not a valid type.
Multiplication of arbitrary quaternions 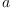 and
and 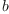
fricas
a:=Σ(sb('a,[i])*𝐞.i, i,1..dim)
There are no library operations named 𝐞
Use HyperDoc Browse or issue
)what op 𝐞
to learn if there is any operation containing " 𝐞 " in its name.
Cannot find a definition or applicable library operation named 𝐞
with argument type(s)
PositiveInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
There are no library operations named 𝐞
Use HyperDoc Browse or issue
)what op 𝐞
to learn if there is any operation containing " 𝐞 " in its name.
Cannot find a definition or applicable library operation named 𝐞
with argument type(s)
PositiveInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
Multiplication is Associative
fricas
test(
( Y! J ) / _
( Y ) = _
( I Y ) / _
( Y! ) )
There are no library operations named Y!
Use HyperDoc Browse or issue
)what op Y!
to learn if there is any operation containing " Y! " in its name.
Cannot find a definition or applicable library operation named Y!
with argument type(s)
Variable(J)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
A scalar product is denoted by the (2,0)-tensor
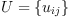
fricas
U:=Σ(Σ(script('u,[[],[i,j]])*𝐝.i*($/𝐝.j), i,1..dim), j,1..dim)
There are no library operations named 𝐝
Use HyperDoc Browse or issue
)what op 𝐝
to learn if there is any operation containing " 𝐝 " in its name.
Cannot find a definition or applicable library operation named 𝐝
with argument type(s)
PositiveInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
There are no library operations named 𝐝
Use HyperDoc Browse or issue
)what op 𝐝
to learn if there is any operation containing " 𝐝 " in its name.
Cannot find a definition or applicable library operation named 𝐝
with argument type(s)
PositiveInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
Definition 1
We say that the scalar product is associative if the tensor
equation holds:
Y = Y
U U
In other words, if the (3,0)-tensor:
(three-point function) is zero.
How should we color this?
(13.0,3.8)
\psline[linewidth=0.04cm](11.4,2.6)(13.0,4.2)
\psline[linewidth=0.04cm](13.0,4.2)(13.4,4.2)
\psline[linewidth=0.04cm](13.4,4.2)(13.4,0.4)
\psline[linewidth=0.04cm](13.0,4.2)(13.0,1.0)
\psline[linewidth=0.04cm](13.4,0.4)(13.0,0.4)
\psline[linewidth=0.04cm](13.0,0.4)(10.4,3.2)
\psline[linewidth=0.04cm](13.4,0.4)(10.8,3.2)
\psline[linewidth=0.04cm](10.4,1.6)(10.4,0.4)
\psline[linewidth=0.04cm](10.8,1.6)(10.8,0.4)
\psline[linewidth=0.04cm](10.4,3.2)(10.4,4.2)
\psline[linewidth=0.04cm](10.8,3.2)(10.8,4.2)
\psline[linewidth=0.04cm](10.8,1.6)(11.4,2.2)
\psline[linewidth=0.04cm](10.4,1.6)(11.2,2.4)
\psline[linewidth=0.04cm](10.4,0.4)(10.8,0.4)
\psline[linewidth=0.03cm](10.4,4.2)(10.8,4.2)
\psline[linewidth=0.03cm](6.8,4.2)(6.8,0.4)
\psline[linewidth=0.03cm](7.1850057,4.2)(7.1850057,0.41349542)
\psline[linewidth=0.03cm](6.8,0.41349542)(7.1850057,0.41349542)
\psline[linewidth=0.03cm](6.8,4.2)(7.2,4.2)
\usefont{T1}{ptm}{m}{n}
\rput(8.315937,2.335){\large \psframebox*[framesep=0, boxsep=false,fillcolor=white] {=}}
\psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](13.2,4.2)(13.2,0.8)
\psline[linewidth=0.04cm](2.4,2.4)(1.0,3.8)
\psline[linewidth=0.04cm](2.6,2.6)(1.0,4.2)
\psline[linewidth=0.04cm](1.0,4.2)(0.6,4.2)
\psline[linewidth=0.04cm](0.6,4.2)(0.6,0.4)
\psline[linewidth=0.04cm](1.0,4.2)(1.0,1.0)
\psline[linewidth=0.04cm](0.6,0.4)(1.0,0.4)
\psline[linewidth=0.04cm](1.0,0.4)(3.6,3.2)
\psline[linewidth=0.04cm](0.6,0.4)(3.2,3.2)
\psline[linewidth=0.04cm](3.6,1.6)(3.6,0.4)
\psline[linewidth=0.04cm](3.2,1.6)(3.2,0.4)
\psline[linewidth=0.04cm](3.6,3.2)(3.6,4.2)
\psline[linewidth=0.04cm](3.2,3.2)(3.2,4.2)
\psline[linewidth=0.04cm](3.2,1.6)(2.6,2.2)
\psline[linewidth=0.04cm](3.6,1.6)(2.8,2.4)
\psline[linewidth=0.04cm](3.6,0.4)(3.2,0.4)
\psline[linewidth=0.03cm](3.6,4.2)(3.2,4.2)
\psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](0.8,4.2)(0.8,0.8)
\usefont{T1}{ptm}{m}{n}
\rput(5.5159373,2.335){\large \psframebox*[framesep=0, boxsep=false,fillcolor=white] {=}}
\psline[linewidth=0.03cm,linestyle=dotted,dotsep=0.16cm](0.0,1.6)(14.0,1.6)
\psline[linewidth=0.03cm,linestyle=dotted,dotsep=0.16cm](0.0,3.2)(14.0,3.2)
\usefont{T1}{ptm}{m}{n}
\rput(6.9159374,-2.265){\large \psframebox*[framesep=0, boxsep=false,fillcolor=white] {=}}
\psline[linewidth=0.04cm](4.2,-1.4)(3.2,-0.4)
\psline[linewidth=0.04cm](4.6,-1.4)(3.6,-0.4)
\psline[linewidth=0.04cm](3.6,-0.4)(3.2,-0.4)
\psline[linewidth=0.04cm](3.2,-0.4)(3.2,-4.2)
\psline[linewidth=0.04cm](3.6,-0.8)(3.6,-3.6)
\psline[linewidth=0.04cm](3.2,-4.2)(3.6,-4.2)
\psline[linewidth=0.04cm](3.6,-4.2)(4.6,-3.0)
\psline[linewidth=0.04cm](3.2,-4.2)(4.2,-3.0)
\psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](3.4,-0.8)(3.4,-4.0)
\psline[linewidth=0.03cm](4.2,-1.4)(4.2,-3.0)
\psline[linewidth=0.03cm](4.6,-1.4)(4.6,-3.0)
\psline[linewidth=0.04cm](9.6,-1.4)(10.6,-0.4)
\psline[linewidth=0.04cm](9.2,-1.4)(10.2,-0.4)
\psline[linewidth=0.04cm](10.2,-0.4)(10.6,-0.4)
\psline[linewidth=0.04cm](10.6,-0.4)(10.6,-4.2)
\psline[linewidth=0.04cm](10.2,-0.8)(10.2,-3.6)
\psline[linewidth=0.04cm](10.6,-4.2)(10.2,-4.2)
\psline[linewidth=0.04cm](10.2,-4.2)(9.2,-3.0)
\psline[linewidth=0.04cm](10.6,-4.2)(9.6,-3.0)
\psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](10.4,-0.8)(10.4,-4.0)
\psline[linewidth=0.03cm](9.6,-1.4)(9.6,-3.0)
\psline[linewidth=0.03cm](9.2,-1.4)(9.2,-3.0)
\end{pspicture}
}
\scalebox{1} % Change this value to rescale the drawing.
{
\begin{pspicture}(0,-4.22)(14.015,4.22)
\psline[linewidth=0.04cm](11.6,2.4)(13.0,3.8)
\psline[linewidth=0.04cm](11.4,2.6)(13.0,4.2)
\psline[linewidth=0.04cm](13.0,4.2)(13.4,4.2)
\psline[linewidth=0.04cm](13.4,4.2)(13.4,0.4)
\psline[linewidth=0.04cm](13.0,4.2)(13.0,1.0)
\psline[linewidth=0.04cm](13.4,0.4)(13.0,0.4)
\psline[linewidth=0.04cm](13.0,0.4)(10.4,3.2)
\psline[linewidth=0.04cm](13.4,0.4)(10.8,3.2)
\psline[linewidth=0.04cm](10.4,1.6)(10.4,0.4)
\psline[linewidth=0.04cm](10.8,1.6)(10.8,0.4)
\psline[linewidth=0.04cm](10.4,3.2)(10.4,4.2)
\psline[linewidth=0.04cm](10.8,3.2)(10.8,4.2)
\psline[linewidth=0.04cm](10.8,1.6)(11.4,2.2)
\psline[linewidth=0.04cm](10.4,1.6)(11.2,2.4)
\psline[linewidth=0.04cm](10.4,0.4)(10.8,0.4)
\psline[linewidth=0.03cm](10.4,4.2)(10.8,4.2)
\psline[linewidth=0.03cm](6.8,4.2)(6.8,0.4)
\psline[linewidth=0.03cm](7.1850057,4.2)(7.1850057,0.41349542)
\psline[linewidth=0.03cm](6.8,0.41349542)(7.1850057,0.41349542)
\psline[linewidth=0.03cm](6.8,4.2)(7.2,4.2)
\usefont{T1}{ptm}{m}{n}
\rput(8.315937,2.335){\large \psframebox*[framesep=0, boxsep=false,fillcolor=white] {=}}
\psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](13.2,4.2)(13.2,0.8)
\psline[linewidth=0.04cm](2.4,2.4)(1.0,3.8)
\psline[linewidth=0.04cm](2.6,2.6)(1.0,4.2)
\psline[linewidth=0.04cm](1.0,4.2)(0.6,4.2)
\psline[linewidth=0.04cm](0.6,4.2)(0.6,0.4)
\psline[linewidth=0.04cm](1.0,4.2)(1.0,1.0)
\psline[linewidth=0.04cm](0.6,0.4)(1.0,0.4)
\psline[linewidth=0.04cm](1.0,0.4)(3.6,3.2)
\psline[linewidth=0.04cm](0.6,0.4)(3.2,3.2)
\psline[linewidth=0.04cm](3.6,1.6)(3.6,0.4)
\psline[linewidth=0.04cm](3.2,1.6)(3.2,0.4)
\psline[linewidth=0.04cm](3.6,3.2)(3.6,4.2)
\psline[linewidth=0.04cm](3.2,3.2)(3.2,4.2)
\psline[linewidth=0.04cm](3.2,1.6)(2.6,2.2)
\psline[linewidth=0.04cm](3.6,1.6)(2.8,2.4)
\psline[linewidth=0.04cm](3.6,0.4)(3.2,0.4)
\psline[linewidth=0.03cm](3.6,4.2)(3.2,4.2)
\psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](0.8,4.2)(0.8,0.8)
\usefont{T1}{ptm}{m}{n}
\rput(5.5159373,2.335){\large \psframebox*[framesep=0, boxsep=false,fillcolor=white] {=}}
\psline[linewidth=0.03cm,linestyle=dotted,dotsep=0.16cm](0.0,1.6)(14.0,1.6)
\psline[linewidth=0.03cm,linestyle=dotted,dotsep=0.16cm](0.0,3.2)(14.0,3.2)
\usefont{T1}{ptm}{m}{n}
\rput(6.9159374,-2.265){\large \psframebox*[framesep=0, boxsep=false,fillcolor=white] {=}}
\psline[linewidth=0.04cm](4.2,-1.4)(3.2,-0.4)
\psline[linewidth=0.04cm](4.6,-1.4)(3.6,-0.4)
\psline[linewidth=0.04cm](3.6,-0.4)(3.2,-0.4)
\psline[linewidth=0.04cm](3.2,-0.4)(3.2,-4.2)
\psline[linewidth=0.04cm](3.6,-0.8)(3.6,-3.6)
\psline[linewidth=0.04cm](3.2,-4.2)(3.6,-4.2)
\psline[linewidth=0.04cm](3.6,-4.2)(4.6,-3.0)
\psline[linewidth=0.04cm](3.2,-4.2)(4.2,-3.0)
\psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](3.4,-0.8)(3.4,-4.0)
\psline[linewidth=0.03cm](4.2,-1.4)(4.2,-3.0)
\psline[linewidth=0.03cm](4.6,-1.4)(4.6,-3.0)
\psline[linewidth=0.04cm](9.6,-1.4)(10.6,-0.4)
\psline[linewidth=0.04cm](9.2,-1.4)(10.2,-0.4)
\psline[linewidth=0.04cm](10.2,-0.4)(10.6,-0.4)
\psline[linewidth=0.04cm](10.6,-0.4)(10.6,-4.2)
\psline[linewidth=0.04cm](10.2,-0.8)(10.2,-3.6)
\psline[linewidth=0.04cm](10.6,-4.2)(10.2,-4.2)
\psline[linewidth=0.04cm](10.2,-4.2)(9.2,-3.0)
\psline[linewidth=0.04cm](10.6,-4.2)(9.6,-3.0)
\psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](10.4,-0.8)(10.4,-4.0)
\psline[linewidth=0.03cm](9.6,-1.4)(9.6,-3.0)
\psline[linewidth=0.03cm](9.2,-1.4)(9.2,-3.0)
\end{pspicture}
}](images/8979932646826338497-16.0px.png)
(2.2,0.1)(2.6,0.1)(2.6,0.9)
\psline[linewidth=0.04cm](2.4,0.3)(2.4,-0.1)
\psbezier[linewidth=0.04](2.4,-0.1)(2.4,-0.9)(3.0,-0.9)(3.0,-0.1)
\psline[linewidth=0.04cm](3.0,-0.1)(3.0,0.9)
\psbezier[linewidth=0.04](4.8,0.9)(4.8,0.1)(4.4,0.1)(4.4,0.9)
\psline[linewidth=0.04cm](4.6,0.3)(4.6,-0.1)
\psbezier[linewidth=0.04](4.6,-0.1)(4.6,-0.9)(4.0,-0.9)(4.0,-0.1)
\psline[linewidth=0.04cm](4.0,-0.1)(4.0,0.9)
\usefont{T1}{ptm}{m}{n}
\rput(3.4948437,0.205){-}
\psline[linewidth=0.04cm](0.6,-0.7)(0.6,0.9)
\psbezier[linewidth=0.04](0.0,-0.1)(0.0,-0.9)(1.2,-0.9)(1.2,-0.1)
\psline[linewidth=0.04cm](0.0,-0.1)(0.0,0.9)
\psline[linewidth=0.04cm](1.2,-0.1)(1.2,0.9)
\usefont{T1}{ptm}{m}{n}
\rput(1.6948438,0.205){=}
\end{pspicture}
}
\scalebox{1} % Change this value to rescale the drawing.
{
\begin{pspicture}(0,-0.92)(4.82,0.92)
\psbezier[linewidth=0.04](2.2,0.9)(2.2,0.1)(2.6,0.1)(2.6,0.9)
\psline[linewidth=0.04cm](2.4,0.3)(2.4,-0.1)
\psbezier[linewidth=0.04](2.4,-0.1)(2.4,-0.9)(3.0,-0.9)(3.0,-0.1)
\psline[linewidth=0.04cm](3.0,-0.1)(3.0,0.9)
\psbezier[linewidth=0.04](4.8,0.9)(4.8,0.1)(4.4,0.1)(4.4,0.9)
\psline[linewidth=0.04cm](4.6,0.3)(4.6,-0.1)
\psbezier[linewidth=0.04](4.6,-0.1)(4.6,-0.9)(4.0,-0.9)(4.0,-0.1)
\psline[linewidth=0.04cm](4.0,-0.1)(4.0,0.9)
\usefont{T1}{ptm}{m}{n}
\rput(3.4948437,0.205){-}
\psline[linewidth=0.04cm](0.6,-0.7)(0.6,0.9)
\psbezier[linewidth=0.04](0.0,-0.1)(0.0,-0.9)(1.2,-0.9)(1.2,-0.1)
\psline[linewidth=0.04cm](0.0,-0.1)(0.0,0.9)
\psline[linewidth=0.04cm](1.2,-0.1)(1.2,0.9)
\usefont{T1}{ptm}{m}{n}
\rput(1.6948438,0.205){=}
\end{pspicture}
}](images/2375189246716000159-16.0px.png)