help links subscribe changes refresh edit

	ClosedLinearOperator
SandBoxClosedLinearOperator ←	↑

SandBoxRibbonCategory

Edit detail for SandBoxRibbonCategory revision 1 of 2

	1 2
Editor: Bill Page Time: 2011/05/26 18:54:29 GMT-7
Note: two-colors

changed:
-
Linear operators over a 2-dimensional vector space representing the algebra of complex numbers

We need the Axiom LinearOperator library.
\begin{axiom}
)library CARTEN ARITY CMONAL CPROP CLOP CALEY
\end{axiom}

Use the following macros for convenient notation
\begin{axiom}
-- summation
macro Σ(x,i,n)==reduce(+,[x for i in n])
-- list
macro Ξ(f,i,n)==[f for i in n]
-- subscript and superscripts
macro sb == subscript
macro sp == superscript
\end{axiom}

𝐋 is the domain of 2-dimensional linear operators over the rational functions ℚ (Expression Integer), i.e. ratio of polynomials with integer coefficients.
\begin{axiom}
dim:=2
macro ℒ == List
macro ℂ == CaleyDickson
macro ℚ == Expression Integer
𝐋 := ClosedLinearOperator(OVAR ['1,'2], ℚ)
𝐞:ℒ 𝐋      := basisOut()
𝐝:ℒ 𝐋      := basisIn()
I:𝐋:=[1]   -- identity for composition
X:𝐋:=[2,1] -- twist
V:𝐋:=ev(1) -- evaluation
Λ:𝐋:=co(1) -- co-evaluation
!:𝐋:=[-1]  -- color change 1 -> 1*
$:𝐋:=dagger ! -- 1* -> 1
J:𝐋:=$/!
test(!/$=I)
equate(eq)==map((x,y)+->(x=y),ravel lhs eq, ravel rhs eq);
\end{axiom}

We want to  be able to implement linear operators with two
"colors" like the following:
$$
\scalebox{1} % Change this value to rescale the drawing.
{
\begin{pspicture}(0,-4.22)(14.015,4.22)
\psline[linewidth=0.04cm](11.6,2.4)(13.0,3.8)
\psline[linewidth=0.04cm](11.4,2.6)(13.0,4.2)
\psline[linewidth=0.04cm](13.0,4.2)(13.4,4.2)
\psline[linewidth=0.04cm](13.4,4.2)(13.4,0.4)
\psline[linewidth=0.04cm](13.0,4.2)(13.0,1.0)
\psline[linewidth=0.04cm](13.4,0.4)(13.0,0.4)
\psline[linewidth=0.04cm](13.0,0.4)(10.4,3.2)
\psline[linewidth=0.04cm](13.4,0.4)(10.8,3.2)
\psline[linewidth=0.04cm](10.4,1.6)(10.4,0.4)
\psline[linewidth=0.04cm](10.8,1.6)(10.8,0.4)
\psline[linewidth=0.04cm](10.4,3.2)(10.4,4.2)
\psline[linewidth=0.04cm](10.8,3.2)(10.8,4.2)
\psline[linewidth=0.04cm](10.8,1.6)(11.4,2.2)
\psline[linewidth=0.04cm](10.4,1.6)(11.2,2.4)
\psline[linewidth=0.04cm](10.4,0.4)(10.8,0.4)
\psline[linewidth=0.03cm](10.4,4.2)(10.8,4.2)
\psline[linewidth=0.03cm](6.8,4.2)(6.8,0.4)
\psline[linewidth=0.03cm](7.1850057,4.2)(7.1850057,0.41349542)
\psline[linewidth=0.03cm](6.8,0.41349542)(7.1850057,0.41349542)
\psline[linewidth=0.03cm](6.8,4.2)(7.2,4.2)
\usefont{T1}{ptm}{m}{n}
\rput(8.315937,2.335){\large \psframebox*[framesep=0, boxsep=false,fillcolor=white] {=}}
\psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](13.2,4.2)(13.2,0.8)
\psline[linewidth=0.04cm](2.4,2.4)(1.0,3.8)
\psline[linewidth=0.04cm](2.6,2.6)(1.0,4.2)
\psline[linewidth=0.04cm](1.0,4.2)(0.6,4.2)
\psline[linewidth=0.04cm](0.6,4.2)(0.6,0.4)
\psline[linewidth=0.04cm](1.0,4.2)(1.0,1.0)
\psline[linewidth=0.04cm](0.6,0.4)(1.0,0.4)
\psline[linewidth=0.04cm](1.0,0.4)(3.6,3.2)
\psline[linewidth=0.04cm](0.6,0.4)(3.2,3.2)
\psline[linewidth=0.04cm](3.6,1.6)(3.6,0.4)
\psline[linewidth=0.04cm](3.2,1.6)(3.2,0.4)
\psline[linewidth=0.04cm](3.6,3.2)(3.6,4.2)
\psline[linewidth=0.04cm](3.2,3.2)(3.2,4.2)
\psline[linewidth=0.04cm](3.2,1.6)(2.6,2.2)
\psline[linewidth=0.04cm](3.6,1.6)(2.8,2.4)
\psline[linewidth=0.04cm](3.6,0.4)(3.2,0.4)
\psline[linewidth=0.03cm](3.6,4.2)(3.2,4.2)
\psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](0.8,4.2)(0.8,0.8)
\usefont{T1}{ptm}{m}{n}
\rput(5.5159373,2.335){\large \psframebox*[framesep=0, boxsep=false,fillcolor=white] {=}}
\psline[linewidth=0.03cm,linestyle=dotted,dotsep=0.16cm](0.0,1.6)(14.0,1.6)
\psline[linewidth=0.03cm,linestyle=dotted,dotsep=0.16cm](0.0,3.2)(14.0,3.2)
\usefont{T1}{ptm}{m}{n}
\rput(6.9159374,-2.265){\large \psframebox*[framesep=0, boxsep=false,fillcolor=white] {=}}
\psline[linewidth=0.04cm](4.2,-1.4)(3.2,-0.4)
\psline[linewidth=0.04cm](4.6,-1.4)(3.6,-0.4)
\psline[linewidth=0.04cm](3.6,-0.4)(3.2,-0.4)
\psline[linewidth=0.04cm](3.2,-0.4)(3.2,-4.2)
\psline[linewidth=0.04cm](3.6,-0.8)(3.6,-3.6)
\psline[linewidth=0.04cm](3.2,-4.2)(3.6,-4.2)
\psline[linewidth=0.04cm](3.6,-4.2)(4.6,-3.0)
\psline[linewidth=0.04cm](3.2,-4.2)(4.2,-3.0)
\psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](3.4,-0.8)(3.4,-4.0)
\psline[linewidth=0.03cm](4.2,-1.4)(4.2,-3.0)
\psline[linewidth=0.03cm](4.6,-1.4)(4.6,-3.0)
\psline[linewidth=0.04cm](9.6,-1.4)(10.6,-0.4)
\psline[linewidth=0.04cm](9.2,-1.4)(10.2,-0.4)
\psline[linewidth=0.04cm](10.2,-0.4)(10.6,-0.4)
\psline[linewidth=0.04cm](10.6,-0.4)(10.6,-4.2)
\psline[linewidth=0.04cm](10.2,-0.8)(10.2,-3.6)
\psline[linewidth=0.04cm](10.6,-4.2)(10.2,-4.2)
\psline[linewidth=0.04cm](10.2,-4.2)(9.2,-3.0)
\psline[linewidth=0.04cm](10.6,-4.2)(9.6,-3.0)
\psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](10.4,-0.8)(10.4,-4.0)
\psline[linewidth=0.03cm](9.6,-1.4)(9.6,-3.0)
\psline[linewidth=0.03cm](9.2,-1.4)(9.2,-3.0)
\end{pspicture} 
}
$$

An example starting with Complex Algebra

The basis consists of the real and imaginary units. We use complex multiplication to form the "multiplication table" as a matrix. Then the structure constants can be obtained by dividing each matrix entry by the list of basis vectors.

Split-complex can be specified by Caley-Dickson parameter (q0 = -1)
\begin{axiom}
--q:=1  -- split-complex
q:=sp('i,[2])
QQ := ℂ(ℚ,'i,q);
\end{axiom}

Basis: Each B.i is a complex number
\begin{axiom}
B:ℒ QQ := map(x +-> hyper x,1$SQMATRIX(dim,ℚ)::ℒ ℒ ℚ)
-- Multiplication table:
M:Matrix QQ := matrix Ξ(Ξ(B.i*B.j, i,1..dim), j,1..dim)
-- Function to divide the matrix entries by a basis element
S(y) == map(x +-> real real(x/y),M)
-- The result is a nested list
ѕ :=map(S,B)::ℒ ℒ ℒ ℚ
-- structure constants form a tensor operator
Y := Σ(Σ(Σ(ѕ(i)(k)(j)*𝐞.i*𝐝.j*($/𝐝.k), i,1..dim), j,1..dim), k,1..dim)
arity Y
Y! := (I,!)/Y
matrix Ξ(Ξ((𝐞.i*𝐞.j)/Y!, i,1..dim), j,1..dim)
\end{axiom}

Multiplication of arbitrary quaternions $a$ and $b$
\begin{axiom}
a:=Σ(sb('a,[i])*𝐞.i, i,1..dim)
b:=Σ(sb('b,[i])*𝐞.i, i,1..dim)
(a,b)/Y!
\end{axiom}

Multiplication is Associative
\begin{axiom}
test(
  (  Y! J ) / _
  (   Y   ) = _
  (  I Y  ) / _
  (   Y!  ) )
\end{axiom}

A scalar product is denoted by the (2,0)-tensor
$U = \{ u_{ij} \}$
\begin{axiom}
U:=Σ(Σ(script('u,[[],[i,j]])*𝐝.i*($/𝐝.j), i,1..dim), j,1..dim)
arity U
\end{axiom}

Definition 1

  We say that the scalar product is *associative* if the tensor
  equation holds::

    Y   =   Y
     U     U

  In other words, if the (3,0)-tensor:

$$
\scalebox{1} % Change this value to rescale the drawing.
{
\begin{pspicture}(0,-0.92)(4.82,0.92)
\psbezier[linewidth=0.04](2.2,0.9)(2.2,0.1)(2.6,0.1)(2.6,0.9)
\psline[linewidth=0.04cm](2.4,0.3)(2.4,-0.1)
\psbezier[linewidth=0.04](2.4,-0.1)(2.4,-0.9)(3.0,-0.9)(3.0,-0.1)
\psline[linewidth=0.04cm](3.0,-0.1)(3.0,0.9)
\psbezier[linewidth=0.04](4.8,0.9)(4.8,0.1)(4.4,0.1)(4.4,0.9)
\psline[linewidth=0.04cm](4.6,0.3)(4.6,-0.1)
\psbezier[linewidth=0.04](4.6,-0.1)(4.6,-0.9)(4.0,-0.9)(4.0,-0.1)
\psline[linewidth=0.04cm](4.0,-0.1)(4.0,0.9)
\usefont{T1}{ptm}{m}{n}
\rput(3.4948437,0.205){-}
\psline[linewidth=0.04cm](0.6,-0.7)(0.6,0.9)
\psbezier[linewidth=0.04](0.0,-0.1)(0.0,-0.9)(1.2,-0.9)(1.2,-0.1)
\psline[linewidth=0.04cm](0.0,-0.1)(0.0,0.9)
\psline[linewidth=0.04cm](1.2,-0.1)(1.2,0.9)
\usefont{T1}{ptm}{m}{n}
\rput(1.6948438,0.205){=}
\end{pspicture} 
}
$$

\begin{equation}
\Phi = \{ \phi^{ijk} = {y^e}_{ij} u_{ek} - u_{ie} {y_e}^{jk} \}
\end{equation}
(three-point function) is zero.

*How should we color this?*

Linear operators over a 2-dimensional vector space representing the algebra of complex numbers

We need the Axiom LinearOperator? library.

axiom

)library CARTEN ARITY CMONAL CPROP CLOP CALEY

   CartesianTensor is now explicitly exposed in frame initial 
   CartesianTensor will be automatically loaded when needed from 
      /var/zope2/var/LatexWiki/CARTEN.NRLIB/CARTEN
   Arity is now explicitly exposed in frame initial 
   Arity will be automatically loaded when needed from 
      /var/zope2/var/LatexWiki/ARITY.NRLIB/ARITY
   ClosedMonoidal is now explicitly exposed in frame initial 
   ClosedMonoidal will be automatically loaded when needed from 
      /var/zope2/var/LatexWiki/CMONAL.NRLIB/CMONAL
   ClosedProp is now explicitly exposed in frame initial 
   ClosedProp will be automatically loaded when needed from 
      /var/zope2/var/LatexWiki/CPROP.NRLIB/CPROP
   ClosedLinearOperator is now explicitly exposed in frame initial 
   ClosedLinearOperator will be automatically loaded when needed from 
      /var/zope2/var/LatexWiki/CLOP.NRLIB/CLOP
   CaleyDickson is now explicitly exposed in frame initial 
   CaleyDickson will be automatically loaded when needed from 
      /var/zope2/var/LatexWiki/CALEY.NRLIB/CALEY

Use the following macros for convenient notation

axiom

-- summation
macro Σ(x,i,n)==reduce(+,[x for i in n])

Type: Void

axiom

-- list
macro Ξ(f,i,n)==[f for i in n]

Type: Void

axiom

-- subscript and superscripts
macro sb == subscript

Type: Void

axiom

macro sp == superscript

Type: Void

𝐋 is the domain of 2-dimensional linear operators over the rational functions ℚ (Expression Integer), i.e. ratio of polynomials with integer coefficients.

axiom

dim:=2

$\label{eq1}2$

(1)

Type: PositiveInteger?

axiom

macro ℒ == List

Type: Void

axiom

macro ℂ == CaleyDickson

Type: Void

axiom

macro ℚ == Expression Integer

Type: Void

axiom

𝐋 := ClosedLinearOperator(OVAR ['1,'2], ℚ)

$\label{eq2}\hbox{\axiomType{ClosedLinearOperator}\ } (\hbox{\axiomType{OrderedVariableList}\ } ([ 1, 2 ]) , \hbox{\axiomType{Expression}\ } (\hbox{\axiomType{Integer}\ }))$

(2)

Type: Type

axiom

𝐞:ℒ 𝐋      := basisOut()

$\label{eq3}\left[{|_{\ 1}}, \:{|_{\ 2}}\right]$

(3)

Type: List(ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer)))

axiom

𝐝:ℒ 𝐋      := basisIn()

$\label{eq4}\left[{|^{\ 1}}, \:{|^{\ 2}}\right]$

(4)

Type: List(ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer)))

axiom

I:𝐋:=[1]   -- identity for composition

$\label{eq5}{|_{\ 1}^{\ 1}}+{|_{\ 2}^{\ 2}}$

(5)

Type: ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer))

axiom

X:𝐋:=[2,1] -- twist

$\label{eq6}{|_{\ 1 \ 1}^{\ 1 \ 1}}+{|_{\ 2 \ 1}^{\ 1 \ 2}}+{|_{\ 1 \ 2}^{\ 2 \ 1}}+{|_{\ 2 \ 2}^{\ 2 \ 2}}$

(6)

Type: ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer))

axiom

V:𝐋:=ev(1) -- evaluation

$\label{eq7}{|^{\ 1 \ 1}}+{|^{\ 2 \ 2}}$

(7)

Type: ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer))

axiom

Λ:𝐋:=co(1) -- co-evaluation

$\label{eq8}{|_{\ 1 \ 1}}+{|_{\ 2 \ 2}}$

(8)

Type: ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer))

axiom

!:𝐋:=[-1]  -- color change 1 -> 1*

$\label{eq9}{|_{\ {1_{\ }^{}}}^{\ 1}}+{|_{\ {2_{\ }^{}}}^{\ 2}}$

(9)

Type: ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer))

axiom

$:𝐋:=dagger ! -- 1* -> 1

$\label{eq10}{|_{\ 1}^{\ {1_{\ }^{}}}}+{|_{\ 2}^{\ {2_{\ }^{}}}}$

(10)

Type: ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer))

axiom

J:𝐋:=$/!

$\label{eq11}{|_{\ {1_{\ }^{}}}^{\ {1_{\ }^{}}}}+{|_{\ {2_{\ }^{}}}^{\ {2_{\ }^{}}}}$

(11)

Type: ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer))

axiom

test(!/$=I)

$\label{eq12} \mbox{\rm true}$

(12)

Type: Boolean

axiom

equate(eq)==map((x,y)+->(x=y),ravel lhs eq, ravel rhs eq);

Type: Void

We want to be able to implement linear operators with two "colors" like the following:

$\scalebox{1} % Change this value to rescale the drawing. { \begin{pspicture}(0,-4.22)(14.015,4.22) \psline[linewidth=0.04cm](11.6,2.4)(13.0,3.8) \psline[linewidth=0.04cm](11.4,2.6)(13.0,4.2) \psline[linewidth=0.04cm](13.0,4.2)(13.4,4.2) \psline[linewidth=0.04cm](13.4,4.2)(13.4,0.4) \psline[linewidth=0.04cm](13.0,4.2)(13.0,1.0) \psline[linewidth=0.04cm](13.4,0.4)(13.0,0.4) \psline[linewidth=0.04cm](13.0,0.4)(10.4,3.2) \psline[linewidth=0.04cm](13.4,0.4)(10.8,3.2) \psline[linewidth=0.04cm](10.4,1.6)(10.4,0.4) \psline[linewidth=0.04cm](10.8,1.6)(10.8,0.4) \psline[linewidth=0.04cm](10.4,3.2)(10.4,4.2) \psline[linewidth=0.04cm](10.8,3.2)(10.8,4.2) \psline[linewidth=0.04cm](10.8,1.6)(11.4,2.2) \psline[linewidth=0.04cm](10.4,1.6)(11.2,2.4) \psline[linewidth=0.04cm](10.4,0.4)(10.8,0.4) \psline[linewidth=0.03cm](10.4,4.2)(10.8,4.2) \psline[linewidth=0.03cm](6.8,4.2)(6.8,0.4) \psline[linewidth=0.03cm](7.1850057,4.2)(7.1850057,0.41349542) \psline[linewidth=0.03cm](6.8,0.41349542)(7.1850057,0.41349542) \psline[linewidth=0.03cm](6.8,4.2)(7.2,4.2) \usefont{T1}{ptm}{m}{n} \rput(8.315937,2.335){\large \psframebox*[framesep=0, boxsep=false,fillcolor=white] {=}} \psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](13.2,4.2)(13.2,0.8) \psline[linewidth=0.04cm](2.4,2.4)(1.0,3.8) \psline[linewidth=0.04cm](2.6,2.6)(1.0,4.2) \psline[linewidth=0.04cm](1.0,4.2)(0.6,4.2) \psline[linewidth=0.04cm](0.6,4.2)(0.6,0.4) \psline[linewidth=0.04cm](1.0,4.2)(1.0,1.0) \psline[linewidth=0.04cm](0.6,0.4)(1.0,0.4) \psline[linewidth=0.04cm](1.0,0.4)(3.6,3.2) \psline[linewidth=0.04cm](0.6,0.4)(3.2,3.2) \psline[linewidth=0.04cm](3.6,1.6)(3.6,0.4) \psline[linewidth=0.04cm](3.2,1.6)(3.2,0.4) \psline[linewidth=0.04cm](3.6,3.2)(3.6,4.2) \psline[linewidth=0.04cm](3.2,3.2)(3.2,4.2) \psline[linewidth=0.04cm](3.2,1.6)(2.6,2.2) \psline[linewidth=0.04cm](3.6,1.6)(2.8,2.4) \psline[linewidth=0.04cm](3.6,0.4)(3.2,0.4) \psline[linewidth=0.03cm](3.6,4.2)(3.2,4.2) \psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](0.8,4.2)(0.8,0.8) \usefont{T1}{ptm}{m}{n} \rput(5.5159373,2.335){\large \psframebox*[framesep=0, boxsep=false,fillcolor=white] {=}} \psline[linewidth=0.03cm,linestyle=dotted,dotsep=0.16cm](0.0,1.6)(14.0,1.6) \psline[linewidth=0.03cm,linestyle=dotted,dotsep=0.16cm](0.0,3.2)(14.0,3.2) \usefont{T1}{ptm}{m}{n} \rput(6.9159374,-2.265){\large \psframebox*[framesep=0, boxsep=false,fillcolor=white] {=}} \psline[linewidth=0.04cm](4.2,-1.4)(3.2,-0.4) \psline[linewidth=0.04cm](4.6,-1.4)(3.6,-0.4) \psline[linewidth=0.04cm](3.6,-0.4)(3.2,-0.4) \psline[linewidth=0.04cm](3.2,-0.4)(3.2,-4.2) \psline[linewidth=0.04cm](3.6,-0.8)(3.6,-3.6) \psline[linewidth=0.04cm](3.2,-4.2)(3.6,-4.2) \psline[linewidth=0.04cm](3.6,-4.2)(4.6,-3.0) \psline[linewidth=0.04cm](3.2,-4.2)(4.2,-3.0) \psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](3.4,-0.8)(3.4,-4.0) \psline[linewidth=0.03cm](4.2,-1.4)(4.2,-3.0) \psline[linewidth=0.03cm](4.6,-1.4)(4.6,-3.0) \psline[linewidth=0.04cm](9.6,-1.4)(10.6,-0.4) \psline[linewidth=0.04cm](9.2,-1.4)(10.2,-0.4) \psline[linewidth=0.04cm](10.2,-0.4)(10.6,-0.4) \psline[linewidth=0.04cm](10.6,-0.4)(10.6,-4.2) \psline[linewidth=0.04cm](10.2,-0.8)(10.2,-3.6) \psline[linewidth=0.04cm](10.6,-4.2)(10.2,-4.2) \psline[linewidth=0.04cm](10.2,-4.2)(9.2,-3.0) \psline[linewidth=0.04cm](10.6,-4.2)(9.6,-3.0) \psline[linewidth=0.03cm,linestyle=dashed,dash=0.16cm 0.16cm](10.4,-0.8)(10.4,-4.0) \psline[linewidth=0.03cm](9.6,-1.4)(9.6,-3.0) \psline[linewidth=0.03cm](9.2,-1.4)(9.2,-3.0) \end{pspicture} }$

An example starting with Complex Algebra

The basis consists of the real and imaginary units. We use complex multiplication to form the "multiplication table" as a matrix. Then the structure constants can be obtained by dividing each matrix entry by the list of basis vectors.

Split-complex can be specified by Caley-Dickson parameter (q0 = -1)

axiom

--q:=1  -- split-complex
q:=sp('i,[2])

$\label{eq13}i^{2}$

(13)

Type: Symbol

axiom

QQ := ℂ(ℚ,'i,q);

Type: Type

Basis: Each B.i is a complex number

axiom

B:ℒ QQ := map(x +-> hyper x,1$SQMATRIX(dim,ℚ)::ℒ ℒ ℚ)

$\label{eq14}\left[ 1, \: i \right]$

(14)

Type: List(CaleyDickson?(Expression(Integer),i,*001i(2)))

axiom

-- Multiplication table:
M:Matrix QQ := matrix Ξ(Ξ(B.i*B.j, i,1..dim), j,1..dim)

$\label{eq15}\left[ \begin{array}{cc} 1 & i \ i & -{i^{2}}$

(15)

Type: Matrix(CaleyDickson?(Expression(Integer),i,*001i(2)))

axiom

-- Function to divide the matrix entries by a basis element
S(y) == map(x +-> real real(x/y),M)

Type: Void

axiom

-- The result is a nested list
ѕ :=map(S,B)::ℒ ℒ ℒ ℚ

axiom

Compiling function S with type CaleyDickson(Expression(Integer),i,
      *001i(2)) -> Matrix(Expression(Integer))

$\label{eq16}\left[{\left[{\left[ 1, \: 0 \right]}, \:{\left[ 0, \: -{i^{2}}\right]}\right]}, \:{\left[{\left[ 0, \: 1 \right]}, \:{\left[ 1, \: 0 \right]}\right]}\right]$

(16)

Type: List(List(List(Expression(Integer))))

axiom

-- structure constants form a tensor operator
Y := Σ(Σ(Σ(ѕ(i)(k)(j)*𝐞.i*𝐝.j*($/𝐝.k), i,1..dim), j,1..dim), k,1..dim)

$\label{eq17}{|_{\ 1}^{\ 1 \ {1_{\ }^{}}}}+{|_{\ 2}^{\ 1 \ {2_{\ }^{}}}}+{|_{\ 2}^{\ 2 \ {1_{\ }^{}}}}-{{i^{2}}\ {|_{\ 1}^{\ 2 \ {2_{\ }^{}}}}}$

(17)

Type: ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer))

axiom

arity Y

$\label{eq18}{+ \ -}\over +$

(18)

Type: ClosedProp?(ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer)))

axiom

Y! := (I,!)/Y

$\label{eq19}{|_{\ 1}^{\ 1 \ 1}}+{|_{\ 2}^{\ 1 \ 2}}+{|_{\ 2}^{\ 2 \ 1}}-{{i^{2}}\ {|_{\ 1}^{\ 2 \ 2}}}$

(19)

Type: ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer))

axiom

matrix Ξ(Ξ((𝐞.i*𝐞.j)/Y!, i,1..dim), j,1..dim)

$\label{eq20}\left[ \begin{array}{cc} {|_{\ 1}}&{|_{\ 2}} \ {|_{\ 2}}& -{{i^{2}}\ {|_{\ 1}}}$

(20)

Type: Matrix(ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer)))

Multiplication of arbitrary quaternions 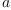and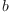

axiom

a:=Σ(sb('a,[i])*𝐞.i, i,1..dim)

$\label{eq21}{{a_{1}}\ {|_{\ 1}}}+{{a_{2}}\ {|_{\ 2}}}$

(21)

Type: ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer))

axiom

b:=Σ(sb('b,[i])*𝐞.i, i,1..dim)

$\label{eq22}{{b_{1}}\ {|_{\ 1}}}+{{b_{2}}\ {|_{\ 2}}}$

(22)

Type: ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer))

axiom

(a,b)/Y!

$\label{eq23}{{\left(-{{i^{2}}\ {a_{2}}\ {b_{2}}}+{{a_{1}}\ {b_{1}}}\right)}\ {|_{\ 1}}}+{{\left({{a_{1}}\ {b_{2}}}+{{a_{2}}\ {b_{1}}}\right)}\ {|_{\ 2}}}$

(23)

Type: ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer))

Multiplication is Associative

axiom

test(
  (  Y! J ) / _
  (   Y   ) = _
  (  I Y  ) / _
  (   Y!  ) )

$\label{eq24} \mbox{\rm true}$

(24)

Type: Boolean

A scalar product is denoted by the (2,0)-tensor $U = \{ u_{ij} \}$

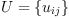
axiom

U:=Σ(Σ(script('u,[[],[i,j]])*𝐝.i*($/𝐝.j), i,1..dim), j,1..dim)

$\label{eq25}{{u^{1, \: 1}}\ {|^{\ 1 \ {1_{\ }^{}}}}}+{{u^{1, \: 2}}\ {|^{\ 1 \ {2_{\ }^{}}}}}+{{u^{2, \: 1}}\ {|^{\ 2 \ {1_{\ }^{}}}}}+{{u^{2, \: 2}}\ {|^{\ 2 \ {2_{\ }^{}}}}}$

(25)

Type: ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer))

axiom

arity U

$\label{eq26}{+ \ -}\over 0$

(26)

Type: ClosedProp?(ClosedLinearOperator?(OrderedVariableList?([1,2]),Expression(Integer)))

Definition 1

We say that the scalar product is associative if the tensor equation holds:

    Y   =   Y
     U     U

In other words, if the (3,0)-tensor:

$\scalebox{1} % Change this value to rescale the drawing. { \begin{pspicture}(0,-0.92)(4.82,0.92) \psbezier[linewidth=0.04](2.2,0.9)(2.2,0.1)(2.6,0.1)(2.6,0.9) \psline[linewidth=0.04cm](2.4,0.3)(2.4,-0.1) \psbezier[linewidth=0.04](2.4,-0.1)(2.4,-0.9)(3.0,-0.9)(3.0,-0.1) \psline[linewidth=0.04cm](3.0,-0.1)(3.0,0.9) \psbezier[linewidth=0.04](4.8,0.9)(4.8,0.1)(4.4,0.1)(4.4,0.9) \psline[linewidth=0.04cm](4.6,0.3)(4.6,-0.1) \psbezier[linewidth=0.04](4.6,-0.1)(4.6,-0.9)(4.0,-0.9)(4.0,-0.1) \psline[linewidth=0.04cm](4.0,-0.1)(4.0,0.9) \usefont{T1}{ptm}{m}{n} \rput(3.4948437,0.205){-} \psline[linewidth=0.04cm](0.6,-0.7)(0.6,0.9) \psbezier[linewidth=0.04](0.0,-0.1)(0.0,-0.9)(1.2,-0.9)(1.2,-0.1) \psline[linewidth=0.04cm](0.0,-0.1)(0.0,0.9) \psline[linewidth=0.04cm](1.2,-0.1)(1.2,0.9) \usefont{T1}{ptm}{m}{n} \rput(1.6948438,0.205){=} \end{pspicture} }$

$\label{eq27} \Phi = \{ \phi^{ijk} = {y^e}_{ij} u_{ek} - u_{ie} {y_e}^{jk} \}$

(27)

(three-point function) is zero.

How should we color this?