Edit detail for SandBoxJacobiDiagFloat revision 1 of 1

(1) -> PI ==> PositiveInteger

NN ==> NonNegativeInteger

IF ==> Float

VIF ==> Vector Float

MIF ==> Matrix Float

free eps

eps:Float:=0.000000001

(1)

free maxIter

maxIter:PI:=1000

(2)

maxInd(k:PI,n:NN,S:MIF):PI ==
  m:PI:=k+1
  for i in k+2..n repeat
    if abs(S(k,i)) > abs(S(k,m)) then m:=i::PI
  return m

   Function declaration maxInd : (PositiveInteger, NonNegativeInteger, 
      Matrix(Float)) -> PositiveInteger has been added to workspace.

jacobi(M:MIF):Record(ev:VIF,EV:MIF) ==
  not square? M => error
  S:MIF:=copy M
  --eps:Float:=0.000000001
  n:NN:=nrows S
  i:PI; k:PI; l:PI; m:PI
  state:NN
  s:IF;c:IF;t:IF;p:IF;y:IF;d:IF;r:IF
  ind:List(PI):=[1 for i in 1..n]
  changed:List Boolean:=[false for i in 1..n]
  e:VIF:=new(n,0$IF)$VIF
  E:MIF:=new(n,n,0$IF)$MIF
  E:=diagonalMatrix [1$IF for i in 1..n]
  A:IF; B:IF
  count:NN:=0
  state:=n
  for k in 1..n repeat
    ind.k:=maxInd(k,n,S)
    e.k:=S(k,k)
    changed.k:=true
  while (state ~= 0) and (count < maxIter) repeat
    m:=1
    for k in 2..n-1 repeat
      if abs(S(k,ind.k)) > abs(S(m,ind.m)) then
        m:=k
    k:=m
    l:=ind.m
    p:=S(k,l)
    --
    y:=(e.l - e.k)/2
    d:=abs(y)+sqrt(p^2+y^2)
    r:=sqrt(p^2+d^2)
    c:=d*recip(r)
    s:=p*recip(r)
    t:=p^2*recip(d)
    if y < 0$Float then
      s:=-s
      t:=-t
    S(k,l):=0$IF
    --
    y:IF:=e.k
    e.k:=y-t
    if changed.k and abs(t)<= eps then
      changed.k:=false
      state:=state-1
    else
      if (not changed.k) and abs(t)> eps then
        changed.k:=true
        state:=state+1
    --
    y:IF:=e.l
    e.l:=y+t
    if changed.l and abs(t)<= eps then
      changed.l:=false
      state:=state-1
    else
      if (not changed.l) and abs(t)> eps then
        changed.l:=true
        state:=state+1
    --
    for i in 1..k-1 repeat
      A:=S(i,k); B:=S(i,l)
      S(i,k):=c*A-s*B
      S(i,l):=s*A+c*B
    for i in k+1..l-1 repeat
      A:=S(k,i); B:=S(i,l)
      S(k,i):=c*A-s*B
      S(i,l):=s*A+c*B
    for i in l+1..n repeat
      A:=S(k,i); B:=S(l,i)
      S(k,i):=c*A-s*B
      S(l,i):=s*A+c*B    
    --
    for i in 1..n repeat
      A:=E(i,k); B:=E(i,l)
      E(i,k):=c*A-s*B
      E(i,l):=s*A+c*B
    --
    ind.k := maxInd(k,n,S)
    ind.l := maxInd(l,n,S)
    --
    count:=count+1
    output([count,state])
  --
  return [e,E]$Record(ev:VIF,EV:MIF)

   Function declaration jacobi : Matrix(Float) -> Record(ev: Vector(
      Float),EV: Matrix(Float)) has been added to workspace.

S0:= matrix [[4,-30,60,-35], [-30,300,-675,420], 
             [60,-675,1620,-1050],[-35,420,-1050,700]]

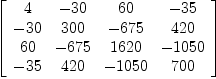(3)

M:=map(s+->s::Float,S0)

(4)

R:=jacobi(M)

Compiling function maxInd with type (PositiveInteger, 
      NonNegativeInteger, Matrix(Float)) -> PositiveInteger

Compiling function jacobi with type Matrix(Float) -> Record(ev: 
      Vector(Float),EV: Matrix(Float))

Compiling function G39 with type Integer -> Boolean

Compiling function G41 with type NonNegativeInteger -> Boolean 
   [1, 4]
   [2, 4]
   [3, 4]
   [4, 4]
   [5, 4]
   [6, 4]
   [7, 4]
   [8, 4]
   [9, 4]
   [10, 4]
   [11, 4]
   [12, 4]
   [13, 2]
   [14, 1]
   [15, 0]

(5)

-- Eigenvalues
R.ev

(6)

-- Eigenvectors
R.EV

(7)

checkResult(R,M) ==
  n:=nrows M
  for i in 1..n repeat
    v:=column(R.EV,i)
    d:=M*v-R.ev.i*v
    output(sqrt(dot(d,d)))

checkResult(R,M)

Compiling function checkResult with type (Record(ev: Vector(Float),
      EV: Matrix(Float)), Matrix(Float)) -> Void 
   0.5525209110_3822153225 E -10
   0.2051229718_0345356366 E -6
   0.2051229643_5393269185 E -6
   0.2534588919_4236924534 E -13