|
|
|
last edited 7 years ago by pagani |
Edit detail for SandBoxFORMAN revision 1 of 1
| 1 | ||
|
Editor: pagani
Time: 2018/07/16 21:33:06 GMT+0 |
||
| Note: | ||
changed: - \begin{spad} )abbrev package FORMAN FormalManipulations ++ Author: Kurt Pagani ++ Date Created: Tue Jun 19 19:09:16 CEST 2018 ++ License: BSD ++ References: ++ Description: ++ Interactive Computer Manipulation of Formal Sums ++ (Thesis format: Monograph) by Nivedita Patil ++ Graduate Program in Computer Science ++ A thesis submitted in partial fulfillment of the requirements for the ++ degree of Master of Science ++ The School of Graduate and Postdoctoral Studies ++ The University of Western Ontario ++ London, Ontario, Canada, (C) Nivedita Patil 2010 ++ http://www.csd.uwo.ca/~watt/home/students/theses/NPatil2010-msc.pdf ++ ++ Abstract: ++ The goal of the thesis is to explore how computer algebra systems can ++ be augmented to allow user-guided transformation and simplification of ++ expressions involving symbolic summation. Mathematical expressions ++ represented as trees are one of the data objects of computer algebra ++ systems. By accessing and manipulating these data objects we can simplify ++ and transform expressions involving symbolic summation. To choose what ++ transformations to be performed is under the discretion of the user. We ++ present a conceptual framework to perform transformations on expressions ++ involving symbolic summation. This is done by creating a set of library ++ functions for interactive manipulation of formal sums. We base our design ++ on the properties of summation. This idea is also extended to other ++ associative operators such as product and definite integral. ++ ++ Keywords: ++ Formal Sums, Computer Algebra System, Associative Operators. ++ FormalManipulations(R) : Exports == Implementation where R:Join(Comparable,IntegralDomain) X ==> Expression R PI ==> PositiveInteger UK ==> Union(Kernel X,"failed") KX ==> Kernel X SX ==> Segment X SBX ==> SegmentBinding X --PINT ==> Polynomial(Integer) --SBPINT ==> SegmentBinding(PINT) Exports == with splitOp : (X,X) -> X multiplyOp : (X,X) -> X splitFunctions : X -> X takeNTermsHigh : (X,X) -> X takeNTermsLow : (X,X) -> X shiftNTerms : (X,X) -> X splitTermsEvenOdd : X -> X reverseOrder : X -> X --splitSum : (X,X) -> X --coerce : % -> OutputForm Implementation == add kernelHandler(x) ==> -- macro mk:UK:=mainKernel(x) if mk case KX then K:KX:=mk else return x A:List X:=argument K v:Symbol:=retract(A.3)@Symbol splitSum(x:X,s:X):X == kernelHandler(x) S1:=summation(subst(A.1,A.2=A.3),equation(v,segment(A.4,s)$SX)$SBX) S2:=summation(subst(A.1,A.2=A.3),equation(v,segment(s+1,A.5)$SX)$SBX) S1+S2 multiplySum(x:X,s:X):X == kernelHandler(x) summation(s*subst(A.1,A.2=A.3),equation(v,segment(A.4,A.5)$SX)$SBX) splitFunctionSum(x:X):X == kernelHandler(x) B:Union(List(X),"failed"):=isPlus(A.1) if B case List(X) then r:SBX:=equation(v,segment(A.4,A.5)$SX)$SBX reduce(_+,[summation(subst(B.j,A.2=A.3),r) for j in 1..#B]) else x takeNTermsHighSum(x:X,n:X):X == kernelHandler(x) summation(subst(A.1,A.2=A.3),equation(v,segment(A.5-n+1,A.5)$SX)$SBX) takeNTermsLowSum(x:X,n:X):X == kernelHandler(x) summation(subst(A.1,A.2=A.3),equation(v,segment(A.4,A.4+n-1)$SX)$SBX) shiftNTermsSum(x:X,n:X):X == kernelHandler(x) summation(subst(A.1,A.2=A.3-n),equation(v,segment(A.4+n,A.5+n)$SX)$SBX) sfloor(x:X):X == f:BasicOperator := operator('floor,1) if R has RetractableTo(Integer) then rx:Union(Fraction Integer, "failed"):=retractIfCan(x) if rx case Fraction(Integer) then return floor(rx)::X f(x) sceiling(x:X):X == c:BasicOperator := operator('ceiling,1) if R has RetractableTo(Integer) then rx:Union(Fraction Integer, "failed"):=retractIfCan(x) if rx case Fraction(Integer) then return ceiling(rx)::X c(x) startsplit(x:X):X == ss:BasicOperator := operator('startSplit,1) if R has RetractableTo(Integer) then rx:Union(Integer, "failed"):=retractIfCan(x) if rx case Integer then q:Fraction Integer:=rx/2 if odd? rx then return ceiling(q)::X else return (1+ceiling(q))::X ss(x) splitTermsEvenOddSum(x:X):X == kernelHandler(x) s1:SX:=segment(sceiling(A.4/2::X),sfloor(A.5/2::X))$SX s2:SX:=segment(startsplit(A.4), sceiling(A.5/2::X))$SX S1:=summation(subst(A.1,A.2=2*A.3),equation(v,s1)$SBX) S2:=summation(subst(A.1,A.2=2*A.3-1),equation(v,s2)$SBX) S1+S2 -- TODO: complete this -- DONE: see ref reverseOrderSum(x:X):X == kernelHandler(x) s:SX:=segment(A.4-A.4,A.5-A.4)$SX summation(subst(A.1,A.2=A.5-A.3),equation(v,s)$SBX) -- -- Exports -- splitOp(x:X,s:X):X == is?(x,'%defsum) => splitSum(x,s) return x multiplyOp(x:X,s:X):X == is?(x,'%defsum) => multiplySum(x,s) return x splitFunctions(x:X):X == is?(x,'%defsum) => splitFunctionSum(x) return x takeNTermsHigh(x:X,n:X):X == is?(x,'%defsum) => takeNTermsHighSum(x,n) return x takeNTermsLow(x:X,n:X):X == is?(x,'%defsum) => takeNTermsLowSum(x,n) return x shiftNTerms(x:X,n:X):X == is?(x,'%defsum) => shiftNTermsSum(x,n) return x splitTermsEvenOdd(x:X):X == is?(x,'%defsum) => splitTermsEvenOddSum(x) return x reverseOrder(x:X):X == is?(x,'%defsum) => reverseOrderSum(x) return x -- X := operator 'X ; T:=summation(X(s),s=a..b) -- P:=summation(X(s)*x^s,s=0..b) -- f(n)==eval(P,b=n) -- D(P,x,2) -- name mainKernel(P) ->> %defsum \end{spad} Tests (changes fricas 1.2 -> 1.3.+) \begin{axiom} X := operator 'X T:=summation(X(s),s=a..b) T2:=multiplyOp(T,x^s) T3:= D(T2,x) T4:=takeNTermsHigh(T3,m) T5:=shiftNTerms(T4,m) T6:=splitOp(T5,k) \end{axiom} OK now; missing functions: CombineSplitOp,GetCoefficient,TakeTermsValue,CombineSplitFunctions,GetNonVariantsOutside,PutMultiplicandsInside
fricas
(1) -> <spad>
fricas
)abbrev package FORMAN FormalManipulations ++ Author: Kurt Pagani ++ Date Created: Tue Jun 19 19:09:16 CEST 2018 ++ License: BSD ++ References: ++ Description: ++ Interactive Computer Manipulation of Formal Sums ++ (Thesis format: Monograph) by Nivedita Patil ++ Graduate Program in Computer Science ++ A thesis submitted in partial fulfillment of the requirements for the ++ degree of Master of Science ++ The School of Graduate and Postdoctoral Studies ++ The University of Western Ontario ++ London,Ontario, Canada, (C) Nivedita Patil 2010 ++ http://www.csd.uwo.ca/~watt/home/students/theses/NPatil2010-msc.pdf ++ ++ Abstract: ++ The goal of the thesis is to explore how computer algebra systems can ++ be augmented to allow user-guided transformation and simplification of ++ expressions involving symbolic summation. Mathematical expressions ++ represented as trees are one of the data objects of computer algebra ++ systems. By accessing and manipulating these data objects we can simplify ++ and transform expressions involving symbolic summation. To choose what ++ transformations to be performed is under the discretion of the user. We ++ present a conceptual framework to perform transformations on expressions ++ involving symbolic summation. This is done by creating a set of library ++ functions for interactive manipulation of formal sums. We base our design ++ on the properties of summation. This idea is also extended to other ++ associative operators such as product and definite integral. ++ ++ Keywords: ++ Formal Sums, Computer Algebra System, Associative Operators. ++ FormalManipulations(R) : Exports == Implementation where
R:Join(Comparable,IntegralDomain) X ==> Expression R PI ==> PositiveInteger UK ==> Union(Kernel X, "failed") KX ==> Kernel X SX ==> Segment X SBX ==> SegmentBinding X --PINT ==> Polynomial(Integer) --SBPINT ==> SegmentBinding(PINT)
Exports == with
splitOp : (X,X) -> X multiplyOp : (X, X) -> X splitFunctions : X -> X takeNTermsHigh : (X, X) -> X takeNTermsLow : (X, X) -> X shiftNTerms : (X, X) -> X splitTermsEvenOdd : X -> X reverseOrder : X -> X --splitSum : (X, X) -> X --coerce : % -> OutputForm
Implementation == add
kernelHandler(x) ==> -- macro mk:UK:=mainKernel(x) if mk case KX then K:KX:=mk else return x A:List X:=argument K v:Symbol:=retract(A.3)@Symbol
splitSum(x:X,s:X):X == kernelHandler(x) S1:=summation(subst(A.1, A.2=A.3), equation(v, segment(A.4, s)$SX)$SBX) S2:=summation(subst(A.1, A.2=A.3), equation(v, segment(s+1, A.5)$SX)$SBX) S1+S2
multiplySum(x:X,s:X):X == kernelHandler(x) summation(s*subst(A.1, A.2=A.3), equation(v, segment(A.4, A.5)$SX)$SBX)
splitFunctionSum(x:X):X == kernelHandler(x) B:Union(List(X),"failed"):=isPlus(A.1) if B case List(X) then r:SBX:=equation(v, segment(A.4, A.5)$SX)$SBX reduce(_+, [summation(subst(B.j, A.2=A.3), r) for j in 1..#B]) else x
takeNTermsHighSum(x:X,n:X):X == kernelHandler(x) summation(subst(A.1, A.2=A.3), equation(v, segment(A.5-n+1, A.5)$SX)$SBX)
takeNTermsLowSum(x:X,n:X):X == kernelHandler(x) summation(subst(A.1, A.2=A.3), equation(v, segment(A.4, A.4+n-1)$SX)$SBX)
shiftNTermsSum(x:X,n:X):X == kernelHandler(x) summation(subst(A.1, A.2=A.3-n), equation(v, segment(A.4+n, A.5+n)$SX)$SBX)
sfloor(x:X):X == f:BasicOperator := operator('floor,1) if R has RetractableTo(Integer) then rx:Union(Fraction Integer, "failed"):=retractIfCan(x) if rx case Fraction(Integer) then return floor(rx)::X f(x)
sceiling(x:X):X == c:BasicOperator := operator('ceiling,1) if R has RetractableTo(Integer) then rx:Union(Fraction Integer, "failed"):=retractIfCan(x) if rx case Fraction(Integer) then return ceiling(rx)::X c(x)
startsplit(x:X):X == ss:BasicOperator := operator('startSplit,1) if R has RetractableTo(Integer) then rx:Union(Integer, "failed"):=retractIfCan(x) if rx case Integer then q:Fraction Integer:=rx/2 if odd? rx then return ceiling(q)::X else return (1+ceiling(q))::X ss(x)
splitTermsEvenOddSum(x:X):X == kernelHandler(x) s1:SX:=segment(sceiling(A.4/2::X),sfloor(A.5/2::X))$SX s2:SX:=segment(startsplit(A.4), sceiling(A.5/2::X))$SX S1:=summation(subst(A.1, A.2=2*A.3), equation(v, s1)$SBX) S2:=summation(subst(A.1, A.2=2*A.3-1), equation(v, s2)$SBX) S1+S2 -- TODO: complete this -- DONE: see ref
reverseOrderSum(x:X):X == kernelHandler(x) s:SX:=segment(A.4-A.4,A.5-A.4)$SX summation(subst(A.1, A.2=A.5-A.3), equation(v, s)$SBX)
-- -- Exports -- splitOp(x:X,s:X):X == is?(x, '%defsum) => splitSum(x, s) return x
multiplyOp(x:X,s:X):X == is?(x, '%defsum) => multiplySum(x, s) return x
splitFunctions(x:X):X == is?(x,'%defsum) => splitFunctionSum(x) return x
takeNTermsHigh(x:X,n:X):X == is?(x, '%defsum) => takeNTermsHighSum(x, n) return x
takeNTermsLow(x:X,n:X):X == is?(x, '%defsum) => takeNTermsLowSum(x, n) return x
shiftNTerms(x:X,n:X):X == is?(x, '%defsum) => shiftNTermsSum(x, n) return x
splitTermsEvenOdd(x:X):X == is?(x,'%defsum) => splitTermsEvenOddSum(x) return x
reverseOrder(x:X):X == is?(x,'%defsum) => reverseOrderSum(x) return x
-- X := operator 'X ; T:=summation(X(s),s=a..b) -- P:=summation(X(s)*x^s, s=0..b) -- f(n)==eval(P, b=n) -- D(P, x, 2) -- name mainKernel(P) ->> %defsum</spad>
fricas
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/5640122448356627221-25px001.spad
using old system compiler.
FORMAN abbreviates package FormalManipulations
------------------------------------------------------------------------
initializing NRLIB FORMAN for FormalManipulations
compiling into NRLIB FORMAN
****** Domain: R already in scope
processing macro definition kernelHandler x ==> SEQ(:=(mk: Union(Kernel Expression R,
compiling local multiplySum : (Expression R,
compiling local splitFunctionSum : Expression R -> Expression R
Time: 0.01 SEC.
compiling local takeNTermsHighSum : (Expression R,
compiling local takeNTermsLowSum : (Expression R,
compiling local shiftNTermsSum : (Expression R,
compiling local sfloor : Expression R -> Expression R
****** Domain: R already in scope
augmenting R: (RetractableTo (Integer))
Time: 0 SEC.
compiling local sceiling : Expression R -> Expression R
****** Domain: R already in scope
augmenting R: (RetractableTo (Integer))
Time: 0 SEC.
compiling local startsplit : Expression R -> Expression R
****** Domain: R already in scope
augmenting R: (RetractableTo (Integer))
Time: 0 SEC.
compiling local splitTermsEvenOddSum : Expression R -> Expression R
Time: 0.03 SEC.
compiling local reverseOrderSum : Expression R -> Expression R
Time: 0.01 SEC.
compiling exported splitOp : (Expression R,
compiling exported multiplyOp : (Expression R,
compiling exported splitFunctions : Expression R -> Expression R
Time: 0 SEC.
compiling exported takeNTermsHigh : (Expression R,
compiling exported takeNTermsLow : (Expression R,
compiling exported shiftNTerms : (Expression R,
compiling exported splitTermsEvenOdd : Expression R -> Expression R
Time: 0 SEC.
compiling exported reverseOrder : Expression R -> Expression R
Time: 0 SEC.
(time taken in buildFunctor: 0)
Time: 0 SEC.
Cumulative Statistics for Constructor FormalManipulations
Time: 0.11 seconds
finalizing NRLIB FORMAN
Processing FormalManipulations for Browser database:
--------constructor---------
--->-->FormalManipulations((splitOp ((Expression R) (Expression R) (Expression R)))): Not documented!!!!
--->-->FormalManipulations((multiplyOp ((Expression R) (Expression R) (Expression R)))): Not documented!!!!
--->-->FormalManipulations((splitFunctions ((Expression R) (Expression R)))): Not documented!!!!
--->-->FormalManipulations((takeNTermsHigh ((Expression R) (Expression R) (Expression R)))): Not documented!!!!
--->-->FormalManipulations((takeNTermsLow ((Expression R) (Expression R) (Expression R)))): Not documented!!!!
--->-->FormalManipulations((shiftNTerms ((Expression R) (Expression R) (Expression R)))): Not documented!!!!
--->-->FormalManipulations((splitTermsEvenOdd ((Expression R) (Expression R)))): Not documented!!!!
--->-->FormalManipulations((reverseOrder ((Expression R) (Expression R)))): Not documented!!!!
; compiling file "/var/aw/var/LatexWiki/FORMAN.NRLIB/FORMAN.lsp" (written 01 DEC 2025 09:55:12 PM):
; wrote /var/aw/var/LatexWiki/FORMAN.NRLIB/FORMAN.fasl
; compilation finished in 0:00:00.088
------------------------------------------------------------------------
FormalManipulations is now explicitly exposed in frame initial
FormalManipulations will be automatically loaded when needed from
/var/aw/var/LatexWiki/FORMAN.NRLIB/FORMANTests (changes fricas 1.2 -> 1.3.+)
fricas
X := operator 'X
| (1) |
Type: BasicOperator?
fricas
T:=summation(X(s),s=a..b)
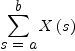 | (2) |
Type: Expression(Integer)
fricas
T2:=multiplyOp(T,x^s)
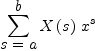 | (3) |
Type: Expression(Integer)
fricas
T3:= D(T2,x)
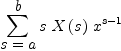 | (4) |
Type: Expression(Integer)
fricas
T4:=takeNTermsHigh(T3,m)
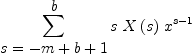 | (5) |
Type: Expression(Integer)
fricas
T5:=shiftNTerms(T4,m)
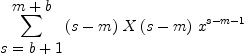 | (6) |
Type: Expression(Integer)
fricas
T6:=splitOp(T5,k)
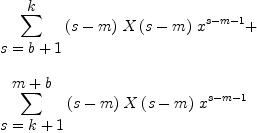 | (7) |
Type: Expression(Integer)
OK now; missing functions: CombineSplitOp?,GetCoefficient?,TakeTermsValue?,CombineSplitFunctions?,GetNonVariantsOutside?,PutMultiplicandsInside?