Einstein Velocity and Non-associative Addition
Reference
- Matolcsi 4.2.3 op. cit.
- In contradistinction to the non-relativistic case and to
our habitual "evidence", the relative velocity of P with
respect to Q is not the opposite of the relative velocity
of Q with respect to P ... It is worth emphasizing this
fact because in most textbooks one takes it for granted
that w(P,Q) and -w(Q,P) are equal: "If an observer moves
with velocity v relative to another then the second observer
moves with velocity -v relative to the first one.".
Nevertheless, no harm comes because vectors are given
there by their components with respect to some convenient
bases and then the components of w(P,Q) and w(Q,P) become
opposite to each other.
Minkowski Package
This code extends the Minkowski package defined on the
previous page SandBox Lorentz Transformations
fricas
(1) -> <aldor>
#include "axiom.as"
#pile
#library minkowski1 "mink1.ao"
EXPR ==> Expression
FRAC ==> Fraction
INT ==> Integer
LIST ==> List
MATRIX ==> Matrix
PI ==> PositiveInteger
NNI ==> NonNegativeInteger
SQMATRIX ==> SquareMatrix
import from INT, NNI
import from MATRIX EXPR INT
import from EXPR INT
import from SQMATRIX(4,EXPR INT)
import from FRAC INT
import from LIST EXPR INT
minkowski2(): with
M: (MATRIX EXPR INT,MATRIX EXPR INT) -> MATRIX EXPR INT
L: SQMATRIX(4,EXPR INT) -> SQMATRIX(4,EXPR INT)
== add
import from minkowski1
inline from minkowski1
-- Something wrong with the import so these defined locally
g():Matrix EXPR INT == diagonalMatrix([-1,1,1,1])$Matrix(EXPR INT)
g(x:Matrix EXPR INT):Matrix EXPR INT == transpose(x)*g()
-- Boost Bivector
M(P:MATRIX EXPR INT,Q:MATRIX EXPR INT):MATRIX EXPR INT ==
(P*g(Q) - Q*g(P))
-- Lorentz Transformation
L(b:SQMATRIX(4,EXPR INT)):SQMATRIX(4,EXPR INT) ==
id := 1$SQMATRIX(4,EXPR INT)
lambda:EXPR(INT) := 1/(1+sqrt(1+1/2*trace(b^2)))
id + b + lambda * b^2</aldor>
fricas
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/mink2.as
using Aldor compiler and options
-O -Fasy -Fao -Flsp -lfricas -Mno-ALDOR_W_WillObsolete -DFriCAS -Y $FRICAS/algebra -I $FRICAS/algebra
Use the system command )set compiler args to change these
options.
The )library system command was not called after compilation.fricas
)lib mink1
fricas
Reading /var/aw/var/LatexWiki/mink1.asy
minkowski1 is now explicitly exposed in frame initial
minkowski1 will be automatically loaded when needed from
/var/aw/var/LatexWiki/mink1fricas
)lib mink2
fricas
Reading /var/aw/var/LatexWiki/mink2.asy
minkowski2 is now explicitly exposed in frame initial
minkowski2 will be automatically loaded when needed from
/var/aw/var/LatexWiki/mink2Objects and velocities
fricas
P:=obs();
>> System error:
#<SB-SYS:FD-STREAM for "file /var/aw/var/LatexWiki/mink1.fasl" {1004BECB53}> is
a fasl file compiled with SBCL 1.0.31, and can't be loaded into SBCL 1.1.1.
Choose three arbitrary basis vectors 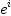 in
in 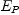 (i.e
such that
(i.e
such that 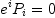 )
)
fricas
e:=matrix [[e1,e2,e3],_
[ 1, 0, 0],_
[ 0, 1, 0],_
[ 0, 0, 1]]
Type: Matrix(Polynomial(Integer))
fricas
e:=eval(e,solve(map(x+->(x=0),members(g(P)*e)),[e1,e2,e3]).1)
There are 1 exposed and 0 unexposed library operations named g
having 1 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op g
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named g
with argument type(s)
Variable(P)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
Express the coefficients of relative velocity u in this basis
fricas
u!:=matrix [[u1],[u2],[u3]]
Type: Matrix(Polynomial(Integer))
fricas
u!:=eval(u!,solve(map(x+->(x=0),members(u-e*u!)),[u1,u2,u3]).1)
There are 9 exposed and 6 unexposed library operations named -
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op -
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named -
with argument type(s)
Variable(u)
Matrix(Polynomial(Integer))
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
The Lorentz transformation transforms the basis 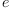 to
to 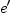 in such
a way that the components of the inverse velocity with respect
to basis
in such
a way that the components of the inverse velocity with respect
to basis 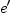 are just minus (-) the components of the velocity
with respect to the basis
are just minus (-) the components of the velocity
with respect to the basis 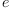 .
.
fricas
e' := L(M(P,Q))*e;
There are 1 exposed and 0 unexposed library operations named M
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op M
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named M
with argument type(s)
Variable(P)
Variable(Q)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
Composition of collinear velocities (again)
For velocity v collinear with reciprocal velocity u' we can
use Einstein's original formula.
Reference: Matolcsi 4.3.4. op. cit.
See SandBoxCategoricalRelativity. Find object L such that
v=w(Q,L) where
fricas
v := alpha*u';
Type: Polynomial(Integer)
fricas
L := b(Q,v);
There are 1 exposed and 0 unexposed library operations named b
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op b
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named b
with argument type(s)
Variable(Q)
Polynomial(Integer)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
First express the coefficients of the composite relative velocity
w(P,L) and the relative velocity v=w(Q,L) in the bases 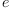 and
and 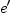
fricas
w!:=matrix [[w1],[w2],[w3]];
Type: Matrix(Polynomial(Integer))
fricas
w!:=eval(w!,solve(map(x+->(x=0),members(w(P,L)-e*w!)),[w1,w2,w3]).1);
There are 1 exposed and 0 unexposed library operations named w
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op w
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named w
with argument type(s)
Variable(P)
Variable(L)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
Then in Einstein's equation we add u! and v! even though they
have different bases:
fricas
abs(u)==sqrt((transpose(u)*u).(1,1))
Type: Void
fricas
Is?( w!=(u!+v!)/(1+abs(u!)*abs(v!)) )
There are 13 exposed and 11 unexposed library operations named +
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op +
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named +
with argument type(s)
Matrix(Polynomial(Integer))
Variable(v!)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
