help links subscribe changes refresh edit

	SandBoxFunctionalSpecialFunction
	↑

SandBoxDiracDelta

last edited 10 years ago by Bill page

Edit detail for SandBoxDiracDelta revision 26 of 40

	1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Editor: Bill page Time: 2014/08/17 16:57:10 GMT+0
Note: Use Wirtinger

changed:
-abs2sqrt := rule abs(a+%i*b)==sqrt(a^2+b^2)
abs(x)==sqrt(x*conjugate(x))
diff(ex,z) == eval(D(eval(ex,z=%conjugate),%conjugate),%conjugate=z)

changed:
-%signum:=differentiate(abs(%z),%z)
-%diracDelta:=differentiate(%signum,%z)/2
%signum:=diff(abs(%z),%z)+diff(abs(%z),conjugate %z)
%diracDelta:=diff(%signum,%z)+diff(%signum,conjugate %z)

changed:
-realSignum:=abs2sqrt(eval(%signum,%z=a+%i*b)+eval(%signum,%z=a-%i*b))/2
realSignum:=eval((eval(%signum,%z=a+%i*b)+eval(%signum,%z=a-%i*b))/2,[conjugate(a)=a,conjugate(b)=b])

changed:
-realDirac:=abs2sqrt(eval(%diracDelta,%z=a+%i*b)+eval(%diracDelta, %z=a-%i*b))/4
realDirac:=eval((eval(%diracDelta,%z=a+%i*b) + eval(%diracDelta, %z=a-%i*b))/2,[conjugate(a)=a,conjugate(b)=b])/2

changed:
-g(x)==eval(abs2sqrt(abs(a+%i*b)/2+abs(a-%i*b)/2),a=x)/2
g(x)==eval((abs(a+%i*b)/2+abs(a-%i*b)/2),a=x)/2

changed:
-gnuDraw(X,Y,"SandBoxDiracDelta1.dat")
gnuDraw(X,Y,"SandBoxDiracDelta.dat")

changed:
-load "SandBoxDiracDelta1.dat"
load "SandBoxDiracDelta.dat"

removed:
-From BillPage Wed Aug 13 15:46:37 +0000 2014
-From: Bill Page
-Date: Wed, 13 Aug 2014 15:46:37 +0000
-Subject: 
-Message-ID: <20140813154637+0000@axiom-wiki.newsynthesis.org>
-
-SandBoxWirtinger

Distributions

We represent distributions as the real part of a complex function in the limit where the imaginary part goes to 0.

Ref.

http://en.wikipedia.org/wiki/Dirac_delta_function

Use new definition of derivative of abs(x) from SandBoxFunctionalSpecialFunction?

fricas

)lib FSPECX

   FunctionalSpecialFunction is now explicitly exposed in frame initial

   FunctionalSpecialFunction will be automatically loaded when needed 
      from /var/aw/var/LatexWiki/FSPECX.NRLIB/FSPECX
abs(x)==sqrt(x*conjugate(x))

Type: Void

fricas

diff(ex,z) == eval(D(eval(ex,z=%conjugate),%conjugate),%conjugate=z)

Type: Void

Derivatives

fricas

%signum:=diff(abs(%z),%z)+diff(abs(%z),conjugate %z)

fricas

Compiling function abs with type Variable(%z) -> Expression(Integer)

fricas

Compiling function diff with type (Expression(Integer),Variable(%z))
       -> Expression(Integer)

fricas

Compiling function diff with type (Expression(Integer),Expression(
      Integer)) -> Expression(Integer)

$\label{eq1}{{\overline \%z}+ \%z}\over{2 \ {\sqrt{\%z \ {\overline \%z}}}}$

(1)

Type: Expression(Integer)

fricas

%diracDelta:=diff(%signum,%z)+diff(%signum,conjugate %z)

$\label{eq2}{-{{\overline \%z}^{2}}+{2 \ \%z \ {\overline \%z}}-{{\%z}^{2}}}\over{4 \ \%z \ {\overline \%z}\ {\sqrt{\%z \ {\overline \%z}}}}$

(2)

Type: Expression(Integer)

Consider the real part of a complex function of for real and with $b \to 0$ .

fricas

realSignum:=eval((eval(%signum,%z=a+%i*b)+eval(%signum,%z=a-%i*b))/2,[conjugate(a)=a,conjugate(b)=b])

$\label{eq3}{a \ {\sqrt{{{b}^{2}}+{{a}^{2}}}}}\over{{{b}^{2}}+{{a}^{2}}}$

(3)

Type: Expression(Complex(Integer))

fricas

signum(x)==eval(realSignum,a=x)

Type: Void

fricas

signum(x)

fricas

Compiling function signum with type Variable(x) -> Expression(
      Complex(Integer))

$\label{eq4}{x \ {\sqrt{{{x}^{2}}+{{b}^{2}}}}}\over{{{x}^{2}}+{{b}^{2}}}$

(4)

Type: Expression(Complex(Integer))

fricas

--
realDirac:=eval((eval(%diracDelta,%z=a+%i*b) + eval(%diracDelta, %z=a-%i*b))/2,[conjugate(a)=a,conjugate(b)=b])/2

$\label{eq5}{{{b}^{2}}\ {\sqrt{{{b}^{2}}+{{a}^{2}}}}}\over{{2 \ {{b}^{4}}}+{4 \ {{a}^{2}}\ {{b}^{2}}}+{2 \ {{a}^{4}}}}$

(5)

Type: Expression(Complex(Integer))

fricas

diracDelta(x)==eval(realDirac,a=x)

Type: Void

fricas

diracDelta(x)

fricas

Compiling function diracDelta with type Variable(x) -> Expression(
      Complex(Integer))

$\label{eq6}{{{b}^{2}}\ {\sqrt{{{x}^{2}}+{{b}^{2}}}}}\over{{2 \ {{x}^{4}}}+{4 \ {{b}^{2}}\ {{x}^{2}}}+{2 \ {{b}^{4}}}}$

(6)

Type: Expression(Complex(Integer))

Properties

fricas

limit( signum(1) ,b=0)

fricas

Compiling function signum with type PositiveInteger -> Expression(
      Complex(Integer))

$\label{eq7}1$

(7)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

limit( signum(-1) ,b=0)

fricas

Compiling function signum with type Integer -> Expression(Complex(
      Integer))

$\label{eq8}- 1$

(8)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

limit( signum(0) ,b=0)

fricas

Compiling function signum with type NonNegativeInteger -> Expression
      (Complex(Integer))

$\label{eq9}0$

(9)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

limit( signum(x)^2 ,b=0)

$\label{eq10}1$

(10)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

limit( diracDelta(1) ,b=0)

fricas

Compiling function diracDelta with type PositiveInteger -> 
      Expression(Complex(Integer))

$\label{eq11}0$

(11)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

limit( diracDelta(-1) ,b=0)

fricas

Compiling function diracDelta with type Integer -> Expression(
      Complex(Integer))

$\label{eq12}0$

(12)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

limit( diracDelta(0) ,b=0)

fricas

Compiling function diracDelta with type NonNegativeInteger -> 
      Expression(Complex(Integer))

$\label{eq13}+ \infty$

(13)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

test( diracDelta(x)=diracDelta(-x) )

fricas

Compiling function diracDelta with type Polynomial(Integer) -> 
      Expression(Complex(Integer))

$\label{eq14} \mbox{\rm true}$

(14)

Type: Boolean

fricas

limit( diracDelta(x)^2 ,b=0)

$\label{eq15}0$

(15)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

integrate(diracDelta(x),x=%minusInfinity..%plusInfinity,"noPole")

$\label{eq16}1$

(16)

Type: Union(f1: OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

f(x)==x+c

Type: Void

fricas

integrate(f(x)*diracDelta(x),x=%minusInfinity..%plusInfinity,"noPole")

fricas

Compiling function f with type Variable(x) -> Polynomial(Integer)

$\label{eq17}c$

(17)

Type: Union(f1: OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

integrate(f(x)*diracDelta(x-t),x=%minusInfinity..%plusInfinity,"noPole")

$\label{eq18}t + c$

(18)

Type: Union(f1: OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

integrate(diracDelta(2*x),x=%minusInfinity..%plusInfinity,"noPole")

$\label{eq19}1 \over 2$

(19)

Type: Union(f1: OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

--
limit( signum(x)*diracDelta(x) ,b=0)

$\label{eq20}0$

(20)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

diracDelta(x^2)

$\label{eq21}{{{b}^{2}}\ {\sqrt{{{x}^{4}}+{{b}^{2}}}}}\over{{2 \ {{x}^{8}}}+{4 \ {{b}^{2}}\ {{x}^{4}}}+{2 \ {{b}^{4}}}}$

(21)

Type: Expression(Complex(Integer))

fricas

limit(%,b=0)

$\label{eq22}0$

(22)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

Heaviside

http://en.wikipedia.org/wiki/Unit_step_function

fricas

realHeaviside:=integrate(diracDelta(a),a)::Expression Complex Integer

fricas

Compiling function diracDelta with type Variable(a) -> Expression(
      Complex(Integer))

$\label{eq23}-{{{b}^{2}}\over{{2 \ a \ {\sqrt{{{b}^{2}}+{{a}^{2}}}}}-{2 \ {{b}^{2}}}-{2 \ {{a}^{2}}}}}$

(23)

Type: Expression(Complex(Integer))

fricas

heavisideStep(x)==eval(realHeaviside,a=x)

Type: Void

fricas

limit( heavisideStep(1), b=0)

fricas

Compiling function heavisideStep with type PositiveInteger -> 
      Expression(Complex(Integer))

$\label{eq24}1$

(24)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

limit( heavisideStep(-1) ,b=0)

fricas

Compiling function heavisideStep with type Integer -> Expression(
      Complex(Integer))

$\label{eq25}0$

(25)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

limit( heavisideStep(0) ,b=0)

fricas

Compiling function heavisideStep with type NonNegativeInteger -> 
      Expression(Complex(Integer))

$\label{eq26}1 \over 2$

(26)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

limit( heavisideStep(x), x=0)

fricas

Compiling function heavisideStep with type Variable(x) -> Expression
      (Complex(Integer))

$\label{eq27}1 \over 2$

(27)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

limit( heavisideStep(x) ,x=%plusInfinity)

$\label{eq28}1$

(28)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

limit( heavisideStep(x) ,x=%minusInfinity)

$\label{eq29}0$

(29)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

test(simplify( (1+signum(x))/2 - heavisideStep(x) ) = 0)

$\label{eq30} \mbox{\rm true}$

(30)

Type: Boolean

fricas

test(limit( integrate(heavisideStep(t),t=%minusInfinity..x, "noPole") - x*heavisideStep(x), b=0) =0)

fricas

Compiling function heavisideStep with type Variable(t) -> Expression
      (Complex(Integer))

$\label{eq31} \mbox{\rm true}$

(31)

Type: Boolean

Problems?

fricas

-- expected 1/abs(alpha)
integrate(diracDelta(alpha*x),x=%minusInfinity..%plusInfinity,"noPole")

$\label{eq32}0$

(32)

Type: Union(f1: OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

-- expected x*abs(x)/2
integrate(abs(x),x)

fricas

Compiling function abs with type Variable(x) -> Expression(Integer)

$\label{eq33}\int^{ \displaystyle x}{{\sqrt{\%A \ {\overline \%A}}}\ {d \%A}}$

(33)

Type: Union(Expression(Integer),...)

fricas

eval(abs2sqrt(abs(a+%i*b)/2+abs(a-%i*b)/2),a=x)

fricas

Compiling function abs with type Polynomial(Complex(Integer)) -> 
      Expression(Complex(Integer)) 
   There are no library operations named abs2sqrt 
      Use HyperDoc Browse or issue
                              )what op abs2sqrt
      to learn if there is any operation containing " abs2sqrt " in its
      name.

   Cannot find a definition or applicable library operation named 
      abs2sqrt with argument type(s) 
                        Expression(Complex(Integer))

      Perhaps you should use "@" to indicate the required return type,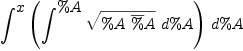 
      or "$" to specify which version of the function you need.
integrate(%,x)

$\label{eq34}\int^{ \displaystyle x}{{\left(\int^{ \displaystyle \%A}{{\sqrt{\%A \ {\overline \%A}}}\ {d \%A}}\right)}\ {d \%A}}$

(34)

Type: Union(Expression(Integer),...)

fricas

limit(%,b=0)

$\label{eq35}\int^{ \displaystyle x}{{\left(\int^{ \displaystyle \%A}{{\sqrt{\%A \ {\overline \%A}}}\ {d \%A}}\right)}\ {d \%A}}$

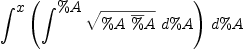(35)

Type: Union(OrderedCompletion?(Expression(Integer)),...)

fricas

-- expected abs(x)
integrate(%signum,%z)

$\label{eq36}\int^{ \displaystyle \%z}{{{{\overline \%A}+ \%A}\over{2 \ {\sqrt{\%A \ {\overline \%A}}}}}\ {d \%A}}$

(36)

Type: Union(Expression(Integer),...)

fricas

integrate(signum(x),x)

$\label{eq37}{-{x \ {\sqrt{{{x}^{2}}+{{b}^{2}}}}}+{{x}^{2}}+{{b}^{2}}}\over{{\sqrt{{{x}^{2}}+{{b}^{2}}}}- x}$

(37)

Type: Union(Expression(Complex(Integer)),...)

fricas

limit(%,b=0)

$\label{eq38}- x$

(38)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

-- expected signum(x)/2
integrate(%diracDelta,%z)

$\label{eq39}\int^{ \displaystyle \%z}{{{-{{\overline \%A}^{2}}+{2 \ \%A \ {\overline \%A}}-{{\%A}^{2}}}\over{4 \ \%A \ {\overline \%A}\ {\sqrt{\%A \ {\overline \%A}}}}}\ {d \%A}}$

(39)

Type: Union(Expression(Integer),...)

fricas

integrate(diracDelta(x^2+y^2), x=%minusInfinity..%plusInfinity, "noPole")

$\label{eq40}\mbox{\tt "failed"}$

(40)

Type: Union(fail: failed,...)

Convolution

fricas

g(x)==eval((abs(a+%i*b)/2+abs(a-%i*b)/2),a=x)/2

Type: Void

fricas

g(y)

fricas

Compiling function g with type Variable(y) -> Expression(Complex(
      Integer))

$\label{eq41}{{\sqrt{{{\left(y +{i \ b}\right)}\ {\overline y}}+{{\left(-{i \ y}+ b \right)}\ {\overline b}}}}+{\sqrt{{{\left(y -{i \ b}\right)}\ {\overline y}}+{{\left({i \ y}+ b \right)}\ {\overline b}}}}}\over 4$

(41)

Type: Expression(Complex(Integer))

fricas

h(x)==heavisideStep(x+1/2)-heavisideStep(x-1/2)

Type: Void

fricas

h(x)

fricas

Compiling function heavisideStep with type Polynomial(Fraction(
      Integer)) -> Expression(Complex(Integer))

fricas

Compiling function h with type Variable(x) -> Expression(Complex(
      Integer))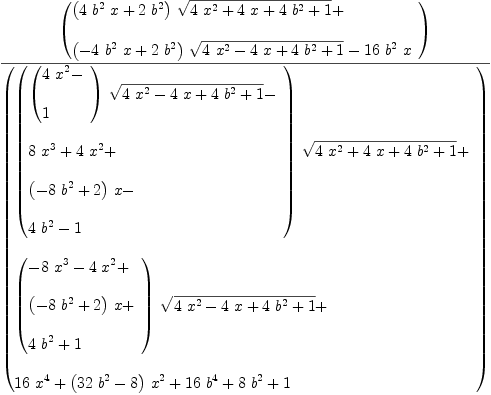

$\label{eq42}{\left( \begin{array}{@{}l} \displaystyle {{\left({4 \ {{b}^{2}}\ x}+{2 \ {{b}^{2}}}\right)}\ {\sqrt{{4 \ {{x}^{2}}}+{4 \ x}+{4 \ {{b}^{2}}}+ 1}}}+ \ \ \displaystyle {{\left(-{4 \ {{b}^{2}}\ x}+{2 \ {{b}^{2}}}\right)}\ {\sqrt{{4 \ {{x}^{2}}}-{4 \ x}+{4 \ {{b}^{2}}}+ 1}}}-{{16}\ {{b}^{2}}\ x}$

(42)

Type: Expression(Complex(Integer))

fricas

conv:=integrate(h(x-y)*g(y),y=%minusInfinity..%plusInfinity,"noPole")

fricas

Compiling function h with type Polynomial(Integer) -> Expression(
      Complex(Integer))

$\label{eq43}\mbox{\tt "failed"}$

(43)

Type: Union(fail: failed,...)

Representing diracDelta as a series of bump functions

fricas

)lib GDRAW

   GnuDraw is now explicitly exposed in frame initial 
   GnuDraw will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/GDRAW.NRLIB/GDRAW
X:=[(x/10)::DFLOAT for x in -100..100 by 1];

Type: List(DoubleFloat?)

fricas

Y:=[eval(diracDelta(x),b=1.0)::DFLOAT for x in X];

fricas

Compiling function diracDelta with type DoubleFloat -> Expression(
      Complex(DoubleFloat))

Type: List(DoubleFloat?)

fricas

gnuDraw(X,Y,"SandBoxDiracDelta.dat")

   Graph data being transmitted to the viewport manager...
   FriCAS2D data being transmitted to the viewport manager...

Type: Void

[terminal=pslatex,terminaloptions=color,scale=1.3]
load "SandBoxDiracDelta.dat"