|
|
|
last edited 7 years ago by pagani |
Edit detail for SandBoxDFORM revision 1 of 1
| 1 | ||
|
Editor: pagani
Time: 2018/07/16 21:49:28 GMT+0 |
||
| Note: | ||
changed: - \begin{spad} )abbrev package DFORM DifferentialForms ++ Author: Kurt Pagani <nilqed@gmail.com> ++ Date Created: October 2014 ++ Revised: Sat Sep 17 17:10:00 CET 2016 ++ License: FriCAS/BSD ++ Description: Basic differential form methods ++ Requirements: DeRhamComplex, FriCAS 1.3 or later. ++ Documentation: Sphinx, folder doc and/or do ++ - [pdf]latex dform.spad -> dvi or pdf file. ++ - run two times to get refs and labels correct. ++ DifferentialForms(R,v) : Exports == Implementation where R: Join(IntegralDomain,Comparable) v: List Symbol X ==> Expression R OF ==> OutputForm DRC ==> DeRhamComplex(R,v) CHC ==> ChainComplex(R,#v) BOP ==> BasicOperator NNI ==> NonNegativeInteger SMR ==> SquareMatrix(#v,X) EAB ==> ExtAlgBasis REA ==> Record(k : EAB, c : X) SGCF ==> SymmetricGroupCombinatoricFunctions Exports == with _* : (List X, List DRC) -> DRC ++ v*w computes the sum of the products v_i * w_i ++ where v_i is a scalar and w_i a differential form. ++ This is for convenience only, just to deal with ++ differential form valued vectors. _* : (List DRC, List DRC) -> DRC ++ w1*w2 computes the sum of the exterior products ++ w1_i * w2_i, where w1,w2 are differential forms. d : DRC -> DRC ++ d w computes the exterior derivative and is just an ++ abbreviation for the fucntion "exteriorDifferential" ++ defined in the domain "DeRhamComplex". one : -> DRC ++ one() gives 1@DeRhamComplex, i.e. "1" as a differential ++ form. This is useful to intern elements of the function ++ ring (just multiply them by one()$DFORM). zero : -> DRC ++ zero() gives the zero form, i.e. 0@DRC. baseForms : () -> List DRC ++ baseForms()$M returns a list of all base forms in the ++ space M=DFORM(Ring,Coordinates). coordVector : () -> List X ++ coordVector()$M returns a list of the coordinates in ++ the space M=DFORM(Ring,Coordinates). coordSymbols : () -> List Symbol ++ coordSymbols()$M returns a list of the coordinates as ++ symbols. This is useful for example if the differential ++ operators "D" are going to be used. vectorField : Symbol -> List X ++ vectorField(V) creates a vector (actually a list) whose ++ components are given by V[j](x[1],...,x[n]), j=1..n, ++ whereby "x" are the space coordinates (possibly not the ++ same symbol). scalarField : Symbol -> X ++ scalarField(s) creates a scalar function s(x[1],...,[n]), ++ whereby "x" are the space coordinates (possibly not the ++ same symbol). covectorField : Symbol -> List DRC ++ covectorField(Y) creates a covector (actually a list) ++ whose components are given by w[j](x[1],...,x[n]), ++ j=1..n. zeroForm : Symbol -> DRC ++ zeroForm(s) creates a zero form with symbol "s". This ++ is the same as scalarField(s)*one(). volumeForm : SMR -> DRC ++ volumeForm(g) returns the volume form with respect to ++ the (pseudo-) metric "g". conjBasisTerm : DRC -> DRC ++ Return the complement of a basis term w.r.t. volumeForm atomizeBasisTerm : DRC -> List DRC ++ Given a basis term, e.g. dx*dy*du, atomizeBasisTerm returns ++ a list of the generators (atoms), i.e. [dx,dy,du] for our example. monomials : NNI -> List DRC ++ List of all monomials of degree p (p in 1..n). ++ This is a basis for Lambda(n,p). hodgeStar : (SMR,DRC) -> DRC ++ computes the Hodge dual of the differential form % with respect ++ to a metric g. dot : (SMR,DRC,DRC) -> X ++ computes the inner product of two differential forms w.r.t. g proj : (NNI,DRC) -> DRC ++ projection to homogeneous terms of degree p interiorProduct : (Vector(X),DRC) -> DRC ++ Calculates the interior product i_X(a) of the vector field X ++ with the differential form a. lieDerivative : (Vector(X),DRC) -> DRC ++ Calculates the Lie derivative L_X(a) of the differential ++ form a with respect to the vector field X. s : SMR -> X ++ s(g) determines the sign of determinant(g) and is related to the ++ signature of g (n=p+q,t=p-q,s=(-)^(n-t)/2 => s=(-)^q. invHodgeStar : (SMR,DRC) -> DRC ++ invHodgeStar is the inverse of hodgeStar. codifferential : (SMR,DRC) -> DRC ++ codifferential(g,x), also known as "delta", computes the ++ co-differential of a form. hodgeLaplacian : (SMR,DRC) -> DRC ++ hodgeLaplacian(g,x) also known as "Laplace-de Rham operator" is ++ defined on any manifold equipped with a (pseudo-) Riemannian ++ metric and is given by d codifferential(g,x)+ codifferential(g, d x). ++ Note that in the Euclidean case hodgeLaplacian = - Laplacian. Implementation == add -- error messages err1:="Metric tensor must be symmetric" err2:="Degenerate metric" err3:="Index out of range" err4:="Not implemented" err5:="Basis term expected" err6:="Zero is not a basis term" -- conversion functions (not very nice ;) eab2li(x:EAB):List(Integer) == x pretend List(Integer) drc2rea(x:DRC):List(REA) == x pretend List(REA) n:NNI:=#v d(f) == exteriorDifferential(f) one () == 1@DRC zero() == 0@DRC baseForms() == [generator(j)$DRC for j in 1..n] coordVector() == [s::X for s in v] coordSymbols() == v vectorField(s:Symbol):List X == ls:=[subscript(s,[j::OF]) for j in 1..n] op:=[operator t for t in ls] x:=[a::X for a in v] [f x for f in op] scalarField(s:Symbol):X == f:=operator s f [a::X for a in v] covectorField(s:Symbol):List DRC == vf:=vectorField(s) [a*1@DRC for a in vf] zeroForm(s:Symbol):DRC == scalarField(s)*1@DRC (l:List(X) * x:List DRC):DRC == l:List DRC:=[l.j * x.j for j in 1..n] reduce(_+,l) (x:List DRC * y:List DRC):DRC == l:List DRC:=[x.j * y.j for j in 1..n] reduce(_+,l) volumeForm(g:SMR):DRC == sqrt(abs(determinant(g)))*reduce(_*,baseForms()) monomials(p:NNI):List DRC == bf:=baseForms() p=0 => [1$DRC] p=1 => bf np:=[reverse subSet(n,p,i)$SGCF for i in 0..binomial(n,p)-1] [reduce(_*,[bf.(1+s.j) for j in 1..p]) for s in np] -- flip 0->1, 1->0 flip(b:EAB):EAB == --bl := convert(b)$EAB bl:=eab2li(b) [(i+1) rem 2 for i in bl]::EAB -- list the positions of a's (a=0,1) in x pos(x:EAB, a:Integer):List(Integer) == y:List(Integer):=eab2li(x) [j for j in 1..#y | y.j=a] -- compute dot of singletons, diagonal g dot1(g:SMR,r:REA, s:REA):X == test(r.k ~= s.k) => 0::X idx := pos(r.k,1) idx = [] => r.c * s.c reduce("*",[1/g(j,j) for j in idx]::List(X)) * r.c * s.c -- compute dot of singleton terms, general symmetric g dot2(g:SMR,r:REA, s:REA):X == pr := pos(r.k,1) -- list positions of 1 in r ps := pos(s.k,1) -- list positions of 1 in s test(#pr ~= #ps) => 0::X -- not same degree => 0 pr = [] => r.c * s.c -- empty pr,ps => product of coefs G := inverse(g)::SMR -- compute the inverse of the metric g test(#pr = 1) => G(pr.1,ps.1)::X * r.c * s.c -- only one element M:Matrix(X) -- the minor M := matrix([[G(pr.i,ps.j)::X for j in 1..#ps] for i in 1..#pr]) determinant(M)::X * r.c * s.c -- export dot(g:SMR,x:DRC,y:DRC):X == not symmetric? g => error(err1) tx:List REA := drc2rea(x) ty:List REA := drc2rea(y) tx = [] or ty = [] => 0::X if diagonal? g then -- better performance a:List(X):=concat[[dot1(g,tx.j,ty.l)::X for j in 1..#tx] for l in 1..#ty] reduce(_+,a) else b:List(X):=concat[[dot2(g,tx.j,ty.l)::X for j in 1..#tx] for l in 1..#ty] reduce(_+,b) proj(p,x) == x=0 => x homogeneous? x and degree(x)=p => x a:=leadingBasisTerm(x) if degree(a)=p then leadingCoefficient(x)*a + proj(p, reductum x) else proj(p, reductum x) conjBasisTerm(x:DRC):DRC == x=0$DRC => error(err6) x ~= leadingBasisTerm(x) => error(err5) t:EAB:=drc2rea(x).1.k l:List(Integer):=exponents(t) m:List(DRC):=[generator(i)$DRC for i in 1..#l | l.i=0] m=[] => 1$DRC reduce(_*,m) atomizeBasisTerm(x:DRC):List(DRC) == x=0$DRC => error(err6) x ~= leadingBasisTerm(x) => error(err5) t:EAB:=drc2rea(x).1.k l:List(Integer):=exponents(t) [generator(i)$DRC for i in 1..#l | l.i=1] intProdBasisTerm(w:Vector X, x:DRC):DRC == x ~= leadingBasisTerm(x) => error(err5) degree(x)=0 => 0$DRC degree(x)=1 => w.position(x,baseForms()) * 1$DRC a:List(DRC):=atomizeBasisTerm(x) b:DRC:=reduce(_*,rest a) -- i_w is an antiderivative => intProdBasisTerm(w,a.1)*b - a.1 * intProdBasisTerm(w,b) interiorProduct(w:Vector X, x:DRC):DRC == x=0$DRC => x leadingCoefficient(x)*intProdBasisTerm(w,leadingBasisTerm(x)) + _ interiorProduct(w, reductum(x)) lieDerivative(w:Vector X,x:DRC):DRC == a := exteriorDifferential(interiorProduct(w,x)) b := interiorProduct(w, exteriorDifferential(x)) a+b eps(x:DRC):X == leadingCoefficient(x*conjBasisTerm(x)) hodgeStarBT(g:SMR,x:DRC):DRC == q:=sqrt(abs(determinant(g))) p:=degree(x) J:=monomials(p) s:=[eps(y)*dot(g,y,x)*conjBasisTerm(y) for y in J] q*reduce(_+,s) hodgeStar(g:SMR,x:DRC):DRC == x=0$DRC => x leadingCoefficient(x)*hodgeStarBT(g,leadingBasisTerm(x)) + _ hodgeStar(g, reductum(x)) s(g:SMR):X == det:X:=determinant g sd:Union(Integer,"failed"):=sign(det)$ElementaryFunctionSign(Integer,X) sd case "failed" => 's?::X sd case Integer => coerce(sd)$X invHodgeStar(g:SMR,x:DRC):DRC == x=0$DRC => x y:DRC:=leadingBasisTerm(x) k:X:=coerce(degree y)$X c:X:=s(g)*(-1)^(k*(coerce(n)$X-k)) leadingCoefficient(x)*hodgeStarBT(g,c*y) + _ invHodgeStar(g, reductum(x)) codifferential(g:SMR,x:DRC):DRC == x=0$DRC => 0 y:DRC:=leadingBasisTerm(x) k:X:=coerce(degree y)$X c:X:=s(g)*(-1)^(coerce(n)$X*(k-1)+1) c*hodgeStar(g,d hodgeStar(g,leadingCoefficient(x)*y)) + _ codifferential(g,reductum(x)) hodgeLaplacian(g:SMR,x:DRC):DRC == d codifferential(g,x)+ codifferential(g, d x) \end{spad} Test flavours \begin{axiom} -- ======================================= -- DFORM tests (package DifferentialForms) -- ======================================= -- Requires: -- .... DeRhamComplex (src/derham.spad) or FriCAS 1.3 or later. -- .... DifferentialForms (dform.spad). -- Version 1.1: 09-ARP-2016 -- Version 1.2: 17-DEC-2016 -- -- FriCAS Computer Algebra System -- Version: FriCAS 1.3.0 -- Timestamp: Don Sep 29 21:26:01 CEST 2016 )set break resume )expose UnittestCount UnittestAux Unittest )expose DFORM ----------------- testsuite "dform" testcase "all" ----------------- ----------- -- Setup -- ----------- n:=7 -- dim of base space (n>=2 !), may change in course N:=91 -- number of tests O ==> OutputForm -- HodgeStar package for DERHAM(R,v) R:=Integer -- Ring v:=[subscript(x,[j::OutputForm]) for j in 1..n] -- (x_1,..,x_n) M:=DFORM(R,v) -- basis 1-forms and coordinate vector dx:=baseForms()$M -- [dx[1],...,dx[n]] x:=coordVector()$M -- [x[1],...,x[n]] xs:=coordSymbols()$M -- as above but as List Symbol (for differentiate, D) -- operator, vector field, scalar field, symbol a:=operator 'a -- operator b:=vectorField(b)$M -- generic vector field [b1(x1..xn),...,bn(x1..xn)] c:=vectorField(c)$M P:=scalarField(P)$M -- scalar field P(x1,..,xn) -- (pseudo-) random form & zeroForm rd:=reduce(_*,[dx.j for j in 1..random(n)$NNI+1]) nf:=zeroForm(nf)$M -- metric g:=diagonalMatrix([1 for i in 1..n])$SquareMatrix(n,EXPR R) -- Euclidean h:=diagonalMatrix(c)$SquareMatrix(n,EXPR R) -- vector field vf:=vector b -- Result list res:List(Boolean):=[false for j in 1..N] -- res.1 := test (dx.1=d(x.1*one()$M)) res.2 := test (#dx = n) res.3 := test (#x = n) res.4 := test (a x = a(x)) res.5 := test (#b = n) -- null Form (i.e. degree 0) res.6 := test (zeroForm('a)$M = a(x)*one()$M) res.7 := test (d zeroForm('a)$M = reduce(_+,[D(a(x),xs.i)*dx.i for i in 1..n])) -- products (à la Flanders, vector forms) res.8 := test ( x*dx = reduce(_+,[x.i*dx.i for i in 1..n])) res.9 := test ( dx * dx = 0) res.10 := test ( (x*dx)*dx = -dx*(x*dx)) -- (co-)vector field res.11 := test (vectorField(W)$M * dx = dx * vectorField(W)$M) res.12 := test (typeOf(vectorField(S)$M)::O=List(Expression(R))::O) res.13 := test (typeOf(covectorField(K)$M)::O=List(DERHAM(R,v))::O) res.14 := test (typeOf(vectorField(W)$M * covectorField(K)$M)::O=DERHAM(R,v)::O) -- dot products w.r.t. g res.15 := reduce(_and,[test ( dot(g,dx.j,dx.j)$M = 1) for j in 1..n]) res.16 := reduce(_and,[test ( dot(g,dx.j,dx.(j+1))$M = 0) for j in 1..n-1]) res.17 := reduce(_and,[test ( dot(g,dx.1*dx.j,dx.1*dx.j)$M = 1) for j in 2..n]) res.18 := reduce(_and,[test ( dot(h,dx.j,dx.j)$M = 1/c.j) for j in 1..n]) res.19 := reduce(_and,[test ( dot(h,dx.j,dx.(j+1))$M = 0) for j in 1..n-1]) res.20 := reduce(_and,[test ( dot(h,dx.1*dx.j,dx.1*dx.j)$M = 1/(c.1*c.j)) _ for j in 2..n]) -- Hodge star res.21 := test (one()$M*hodgeStar(g,1)$M = dot(g,1,1)$M * volumeForm(g)$M) res.22 := test (rd*hodgeStar(g,rd)$M = dot(g,rd,rd)$M * volumeForm(g)$M) res.23 := test (degree(hodgeStar(g,dx.n)$M) = n-1) res.24 := test (one()$M*hodgeStar(h,1)$M = dot(h,1,1)$M * volumeForm(h)$M) res.25 := test (rd*hodgeStar(h,rd)$M = dot(h,rd,rd)$M * volumeForm(h)$M) res.26 := test (degree(hodgeStar(h,dx.n)$M) = n-1) -- Projections res.27 := test (proj(0,nf+b*dx+d(b*dx))$M = nf) res.28 := test (proj(1,nf+b*dx+d(b*dx))$M = b*dx) res.29 := test (proj(2,nf+b*dx+d(b*dx))$M = d(b*dx)) res.30 := test (proj(n,volumeForm(g)$M)$M = volumeForm(g)$M) res.31 := test (proj(random(n)$NNI,volumeForm(g)$M)$M = 0) -- Interior product res.32 := test (interiorProduct(vf,dx.1)$M = b.1) res.33 := test (interiorProduct(vf,dx.n)$M = b.n) res.34 := test (d interiorProduct(vf, volumeForm(g)$M)$M = _ reduce(_+,[D(b.j,xs.j) for j in 1..n])*volumeForm(g)$M) -- Lie derivative res.35 := test ( d interiorProduct(vf,b*dx)$M + _ interiorProduct(vf,d(b*dx))$M = lieDerivative(vf,b*dx)$M) -- Version 1.2 )clear values n R v M x xs dx a b c p g h P vf n:=4 -- dim of base space (n>=2 !) O ==> OutputForm -- HodgeStar package for DERHAM(R,v) R:=Integer -- Ring v:=[subscript(x,[j::OutputForm]) for j in 1..n] -- (x_1,..,x_n) M:=DFORM(R,v) -- basis 1-forms and coordinate vector dx:=baseForms()$M -- [dx[1],...,dx[n]] x:=coordVector()$M -- [x[1],...,x[n]] xs:=coordSymbols()$M -- as above but as List Symbol (for differentiate, D) -- operator, vector field, scalar field, symbol a:=operator 'a -- operator b:=vectorField(b)$M -- generic vector field [b1(x1..xn),...,bn(x1..xn)] c:=vectorField(c)$M P:=scalarField(P)$M -- scalar field P(x1,..,xn) -- metric g:=diagonalMatrix([1 for i in 1..n])$SquareMatrix(n,EXPR R) -- Euclidean h:=diagonalMatrix(c)$SquareMatrix(n,EXPR R) eta:=diagonalMatrix(concat(1,[-1 for i in 2..n]))$SquareMatrix(n,EXPR R) -- vector field vf:=vector b -- macros dV(g) ==> volumeForm(g)$M i(X,w) ==> interiorProduct(X,w)$M L(X,w) ==> lieDerivative(X,w)$M ** w ==> hodgeStar(g,w)$M --- w:=x.1*dx.2-x.2*dx.1 res.36 := test(d w = 2*dx.1*dx.2) res.37 := test(w*w = zero()$M) res.38 := test(i(vf,w) = x.1*b.2-x.2*b.1) res.39 := test(L(vf,w) = d i(vf,w) + i(vf,d w)) res.40 := test(d i(vf,w) + i(vf,d w) - L(vf,w) = zero()$M) res.41 := test(dot(g,w,w)$M = x.1^2+x.2^2) -- div(b) dV res.41 := test(d i(vf,dV(g)) = reduce(_+,[D(b.j,xs.j) for j in 1..n])*dV(g)) res.42 := test(d (P*one()$M) = reduce(_+,[D(P,xs.j)*dx.j for j in 1..n])) res.43 := test(i(vf,d (P*one()$M))= reduce(_+,[D(P,xs.j)*b.j for j in 1..n])*one()$M) res.44 := test(1/dot(g,w,w)$M*w = w*(1/(x.1^2+x.2^2))) res.45 := test(d (1/dot(g,w,w)$M*w) = zero()$M) --- s:=zeroForm('s)$M res.46 := test(d s = totalDifferential(retract s)$DeRhamComplex(Integer,v)) res.47 := test(d s = totalDifferential(retract s)$typeOf(s)) res.48 := test(d (** s) = 0$typeOf(s)) res.49 := test(dot(g,** ( d s),w*dx.2*dx.3)$M = x.2*D(retract s, xs.4)) res.50 := test(d (** ( d s)) = reduce(_+,[D(retract s,xs.j,2) for j in 1..n])*dV(g)) r:=sin(x.1*x.2)*one()$M res.51 := test(d r = x.1*cos(x.1*x.2)*dx.2+x.2*cos(x.1*x.2)*dx.1) res.52 := test(d (** ( d r)) = -(x.1^2+x.2^2)*sin(x.1*x.2)*dV(g)) res.53 := test(** (d (** ( d r))) = -(x.1^2+x.2^2)*sin(x.1*x.2)) res.53 := test(** (d (** ( d r)))::EXPR INT = retract (** (d (** ( d r))))) res.54 := test(eval(** (d (** ( d r)))::EXPR INT,xs.1=%pi) = (-%pi^2-x.2^2)*sin(%pi*x.2)) res.55 := test(eval(eval(** (d (** ( d r)))::EXPR INT,xs.1=%pi) ,xs.2=%pi)=-2*%pi^2*sin(%pi^2)) a(P)*one()$M -- chain diff res.56 := test(d (a(P)*one()$M) = eval(D(a(t),'t),t=P)*d (P*one()$M)) res.57 := test(** invHodgeStar(g,w)$M = w) res.58 := test(invHodgeStar(g,** w)$M = w) res.59 := test(** invHodgeStar(g,** w + dx.1)$M = ** w + dx.1) res.60 := test( ** dV(g) = invHodgeStar(g,dV(g))$M) res.61 := test(** dV(h) ~= invHodgeStar(h,dV(g))$M) res.62 := test( dot(h,w,w)$M = (c.2*x.2^2+c.1*x.1^2)/(c.1*c.2)) res.63 := test( s(g)$M = 1) res.64 := test( s(eta)$M = -1) res.65 := test( s(h)$M = 's? ) -- https://en.wikipedia.org/wiki/Hodge_dual -- Four dimensions res.66 := test( hodgeStar(eta,dx.1)$M = dx.2*dx.3*dx.4) res.67 := test( hodgeStar(eta,dx.2)$M = dx.1*dx.3*dx.4) res.68 := test( hodgeStar(eta,dx.3)$M = dx.1*dx.4*dx.2) res.69 := test( hodgeStar(eta,dx.4)$M = dx.1*dx.2*dx.3) res.70 := test( hodgeStar(eta,dx.1*dx.2)$M = dx.4*dx.3) res.71 := test( hodgeStar(eta,dx.1*dx.3)$M = dx.2*dx.4) res.72 := test( hodgeStar(eta,dx.1*dx.4)$M = dx.3*dx.2) res.73 := test( hodgeStar(eta,dx.2*dx.3)$M = dx.1*dx.4) res.74 := test( hodgeStar(eta,dx.2*dx.4)$M = dx.3*dx.1) res.75 := test( hodgeStar(eta,dx.3*dx.4)$M = dx.1*dx.2) -- codifferential: (delta=(-)^degree(x)*invHodgeStar(g, d hodgeStar(g,x)) res.76 := test(codifferential(g,s*dx.1)$M = -D(retract s,xs.1)*one()$M) res.77 := test(codifferential(g,P*dx.2)$M = -D(P,xs.2)*one()$M) res.78 := test(codifferential(g,s*P*dx.1*dx.2)$M = _ (-P*D(retract s,xs.1)-s*D(P,xs.1))*dx.2+_ (P*D(retract s,xs.2)+s*D(P,xs.2))*dx.1) res.79 := test(codifferential(g,P*w)$M = x.2*D(P,xs.1)*one()$M -_ x.1*D(P,xs.2)*one()$M) res.80 := test(codifferential(g,P*w)$M = _ (-1)^degree(w)*invHodgeStar(g, d hodgeStar(g,P*w)$M)$M) res.81 := test(codifferential(eta,P*w)$M = _ (-1)^degree(w)*invHodgeStar(eta, d hodgeStar(eta,P*w)$M)$M) res.82 := test(codifferential(h,P*w)$M = _ (-1)^degree(w)*invHodgeStar(h, d hodgeStar(h,P*w)$M)$M) res.83 := test(codifferential(h,P*w*dx.3)$M = _ (-1)^degree(w*dx.3)*invHodgeStar(h, d hodgeStar(h,P*w*dx.3)$M)$M) -- the codifferential \delta is (sort of) the adjoint to the differential. -- This doesn’t quite hold, but we can show that it does hold “up to homology”. -- We can calculate their difference times the canonical volume form: res.84 := test((dot(g,d w, dx.1*dx.2)$M -_ dot(g,w,codifferential(g,dx.1*dx.2)$M)$M)*dV(g)= d (w*hodgeStar(g,dx.1*dx.2)$M)) res.85 := test((dot(eta,d w, dx.1*dx.2)$M -_ dot(eta,w,codifferential(eta,dx.1*dx.2)$M)$M)*dV(eta)= d (w*hodgeStar(eta,dx.1*dx.2)$M)) res.86 := test(hodgeLaplacian(g,w*(** w))$M = -4 * dV(g)) res.87 := test(hodgeLaplacian(eta,w*(hodgeStar(eta,w)$M))$M = 4 * dV(eta)) res.88 := test(hodgeLaplacian(h,w*(hodgeStar(h,w)$M))$M =_ d codifferential(h,w*hodgeStar(h,w)$M)$M) res.89 := test(d(vf*dx) * (** d(vf*dx))=dot(g,d(vf*dx),d(vf*dx))$M*dV(g)) -- next is inequality because ** = hodgeStar w.r.t to metric g! res.90 := test(d(vf*dx) * (** d(vf*dx))~=dot(eta,d(vf*dx),d(vf*dx))$M*dV(eta)) -- correct is: res.91 := test(d(vf*dx)*hodgeStar(eta,d(vf*dx))$M=_ dot(eta,d(vf*dx),d(vf*dx))$M*dV(eta)) ------------- -- Results -- ------------- )version )lisp (lisp-implementation-type) )lisp (lisp-implementation-version) res reduce(_and,res) -- dummy statistics [testEquals("res." string(j),"true") for j in 1..N]; statistics() \end{axiom} Some changes necessary: use vectors instead of lists, ...
fricas
(1) -> <spad>
fricas
)abbrev package DFORM DifferentialForms ++ Author: Kurt Pagani <nilqed@gmail.com> ++ Date Created: October 2014 ++ Revised: Sat Sep 17 17:10:00 CET 2016 ++ License: FriCAS/BSD ++ Description: Basic differential form methods ++ Requirements: DeRhamComplex,FriCAS 1.3 or later. ++ Documentation: Sphinx, folder doc and/or do ++ - [pdf]latex dform.spad -> dvi or pdf file. ++ - run two times to get refs and labels correct. ++ DifferentialForms(R, v) : Exports == Implementation where
R: Join(IntegralDomain,Comparable) v: List Symbol
X ==> Expression R OF ==> OutputForm DRC ==> DeRhamComplex(R,v) CHC ==> ChainComplex(R, #v) BOP ==> BasicOperator NNI ==> NonNegativeInteger SMR ==> SquareMatrix(#v, X) EAB ==> ExtAlgBasis REA ==> Record(k : EAB, c : X) SGCF ==> SymmetricGroupCombinatoricFunctions
Exports == with
_* : (List X,List DRC) -> DRC ++ v*w computes the sum of the products v_i * w_i ++ where v_i is a scalar and w_i a differential form. ++ This is for convenience only, just to deal with ++ differential form valued vectors. _* : (List DRC, List DRC) -> DRC ++ w1*w2 computes the sum of the exterior products ++ w1_i * w2_i, where w1, w2 are differential forms. d : DRC -> DRC ++ d w computes the exterior derivative and is just an ++ abbreviation for the fucntion "exteriorDifferential" ++ defined in the domain "DeRhamComplex". one : -> DRC ++ one() gives 1@DeRhamComplex, i.e. "1" as a differential ++ form. This is useful to intern elements of the function ++ ring (just multiply them by one()$DFORM). zero : -> DRC ++ zero() gives the zero form, i.e. 0@DRC. baseForms : () -> List DRC ++ baseForms()$M returns a list of all base forms in the ++ space M=DFORM(Ring, Coordinates). coordVector : () -> List X ++ coordVector()$M returns a list of the coordinates in ++ the space M=DFORM(Ring, Coordinates). coordSymbols : () -> List Symbol ++ coordSymbols()$M returns a list of the coordinates as ++ symbols. This is useful for example if the differential ++ operators "D" are going to be used. vectorField : Symbol -> List X ++ vectorField(V) creates a vector (actually a list) whose ++ components are given by V[j](x[1], ..., x[n]), j=1..n, ++ whereby "x" are the space coordinates (possibly not the ++ same symbol). scalarField : Symbol -> X ++ scalarField(s) creates a scalar function s(x[1], ..., [n]), ++ whereby "x" are the space coordinates (possibly not the ++ same symbol). covectorField : Symbol -> List DRC ++ covectorField(Y) creates a covector (actually a list) ++ whose components are given by w[j](x[1], ..., x[n]), ++ j=1..n. zeroForm : Symbol -> DRC ++ zeroForm(s) creates a zero form with symbol "s". This ++ is the same as scalarField(s)*one(). volumeForm : SMR -> DRC ++ volumeForm(g) returns the volume form with respect to ++ the (pseudo-) metric "g". conjBasisTerm : DRC -> DRC ++ Return the complement of a basis term w.r.t. volumeForm atomizeBasisTerm : DRC -> List DRC ++ Given a basis term, e.g. dx*dy*du, atomizeBasisTerm returns ++ a list of the generators (atoms), i.e. [dx, dy, du] for our example. monomials : NNI -> List DRC ++ List of all monomials of degree p (p in 1..n). ++ This is a basis for Lambda(n, p). hodgeStar : (SMR, DRC) -> DRC ++ computes the Hodge dual of the differential form % with respect ++ to a metric g. dot : (SMR, DRC, DRC) -> X ++ computes the inner product of two differential forms w.r.t. g proj : (NNI, DRC) -> DRC ++ projection to homogeneous terms of degree p interiorProduct : (Vector(X), DRC) -> DRC ++ Calculates the interior product i_X(a) of the vector field X ++ with the differential form a. lieDerivative : (Vector(X), DRC) -> DRC ++ Calculates the Lie derivative L_X(a) of the differential ++ form a with respect to the vector field X. s : SMR -> X ++ s(g) determines the sign of determinant(g) and is related to the ++ signature of g (n=p+q, t=p-q, s=(-)^(n-t)/2 => s=(-)^q. invHodgeStar : (SMR, DRC) -> DRC ++ invHodgeStar is the inverse of hodgeStar. codifferential : (SMR, DRC) -> DRC ++ codifferential(g, x), also known as "delta", computes the ++ co-differential of a form. hodgeLaplacian : (SMR, DRC) -> DRC ++ hodgeLaplacian(g, x) also known as "Laplace-de Rham operator" is ++ defined on any manifold equipped with a (pseudo-) Riemannian ++ metric and is given by d codifferential(g, x)+ codifferential(g, d x). ++ Note that in the Euclidean case hodgeLaplacian = - Laplacian.
Implementation == add
-- error messages err1:="Metric tensor must be symmetric" err2:="Degenerate metric" err3:="Index out of range" err4:="Not implemented" err5:="Basis term expected" err6:="Zero is not a basis term"
-- conversion functions (not very nice ;) eab2li(x:EAB):List(Integer) == x pretend List(Integer) drc2rea(x:DRC):List(REA) == x pretend List(REA)
n:NNI:=#v d(f) == exteriorDifferential(f) one () == 1@DRC zero() == 0@DRC baseForms() == [generator(j)$DRC for j in 1..n] coordVector() == [s::X for s in v] coordSymbols() == v
vectorField(s:Symbol):List X == ls:=[subscript(s,[j::OF]) for j in 1..n] op:=[operator t for t in ls] x:=[a::X for a in v] [f x for f in op]
scalarField(s:Symbol):X == f:=operator s f [a::X for a in v]
covectorField(s:Symbol):List DRC == vf:=vectorField(s) [a*1@DRC for a in vf]
zeroForm(s:Symbol):DRC == scalarField(s)*1@DRC
(l:List(X) * x:List DRC):DRC == l:List DRC:=[l.j * x.j for j in 1..n] reduce(_+,l)
(x:List DRC * y:List DRC):DRC == l:List DRC:=[x.j * y.j for j in 1..n] reduce(_+,l)
volumeForm(g:SMR):DRC == sqrt(abs(determinant(g)))*reduce(_*,baseForms())
monomials(p:NNI):List DRC == bf:=baseForms() p=0 => [1$DRC] p=1 => bf np:=[reverse subSet(n,p, i)$SGCF for i in 0..binomial(n, p)-1] [reduce(_*, [bf.(1+s.j) for j in 1..p]) for s in np]
-- flip 0->1,1->0 flip(b:EAB):EAB == --bl := convert(b)$EAB bl:=eab2li(b) [(i+1) rem 2 for i in bl]::EAB
-- list the positions of a's (a=0,1) in x pos(x:EAB, a:Integer):List(Integer) == y:List(Integer):=eab2li(x) [j for j in 1..#y | y.j=a]
-- compute dot of singletons,diagonal g dot1(g:SMR, r:REA, s:REA):X == test(r.k ~= s.k) => 0::X idx := pos(r.k, 1) idx = [] => r.c * s.c reduce("*", [1/g(j, j) for j in idx]::List(X)) * r.c * s.c
-- compute dot of singleton terms,general symmetric g dot2(g:SMR, r:REA, s:REA):X == pr := pos(r.k, 1) -- list positions of 1 in r ps := pos(s.k, 1) -- list positions of 1 in s test(#pr ~= #ps) => 0::X -- not same degree => 0 pr = [] => r.c * s.c -- empty pr, ps => product of coefs G := inverse(g)::SMR -- compute the inverse of the metric g test(#pr = 1) => G(pr.1, ps.1)::X * r.c * s.c -- only one element M:Matrix(X) -- the minor M := matrix([[G(pr.i, ps.j)::X for j in 1..#ps] for i in 1..#pr]) determinant(M)::X * r.c * s.c
-- export dot(g:SMR,x:DRC, y:DRC):X == not symmetric? g => error(err1) tx:List REA := drc2rea(x) ty:List REA := drc2rea(y) tx = [] or ty = [] => 0::X if diagonal? g then -- better performance a:List(X):=concat[[dot1(g, tx.j, ty.l)::X for j in 1..#tx] for l in 1..#ty] reduce(_+, a) else b:List(X):=concat[[dot2(g, tx.j, ty.l)::X for j in 1..#tx] for l in 1..#ty] reduce(_+, b)
proj(p,x) == x=0 => x homogeneous? x and degree(x)=p => x a:=leadingBasisTerm(x) if degree(a)=p then leadingCoefficient(x)*a + proj(p, reductum x) else proj(p, reductum x)
conjBasisTerm(x:DRC):DRC == x=0$DRC => error(err6) x ~= leadingBasisTerm(x) => error(err5) t:EAB:=drc2rea(x).1.k l:List(Integer):=exponents(t) m:List(DRC):=[generator(i)$DRC for i in 1..#l | l.i=0] m=[] => 1$DRC reduce(_*,m)
atomizeBasisTerm(x:DRC):List(DRC) == x=0$DRC => error(err6) x ~= leadingBasisTerm(x) => error(err5) t:EAB:=drc2rea(x).1.k l:List(Integer):=exponents(t) [generator(i)$DRC for i in 1..#l | l.i=1]
intProdBasisTerm(w:Vector X,x:DRC):DRC == x ~= leadingBasisTerm(x) => error(err5) degree(x)=0 => 0$DRC degree(x)=1 => w.position(x, baseForms()) * 1$DRC a:List(DRC):=atomizeBasisTerm(x) b:DRC:=reduce(_*, rest a) -- i_w is an antiderivative => intProdBasisTerm(w, a.1)*b - a.1 * intProdBasisTerm(w, b)
interiorProduct(w:Vector X,x:DRC):DRC == x=0$DRC => x leadingCoefficient(x)*intProdBasisTerm(w, leadingBasisTerm(x)) + _ interiorProduct(w, reductum(x))
lieDerivative(w:Vector X,x:DRC):DRC == a := exteriorDifferential(interiorProduct(w, x)) b := interiorProduct(w, exteriorDifferential(x)) a+b
eps(x:DRC):X == leadingCoefficient(x*conjBasisTerm(x))
hodgeStarBT(g:SMR,x:DRC):DRC == q:=sqrt(abs(determinant(g))) p:=degree(x) J:=monomials(p) s:=[eps(y)*dot(g, y, x)*conjBasisTerm(y) for y in J] q*reduce(_+, s)
hodgeStar(g:SMR,x:DRC):DRC == x=0$DRC => x leadingCoefficient(x)*hodgeStarBT(g, leadingBasisTerm(x)) + _ hodgeStar(g, reductum(x))
s(g:SMR):X == det:X:=determinant g sd:Union(Integer,"failed"):=sign(det)$ElementaryFunctionSign(Integer, X) sd case "failed" => 's?::X sd case Integer => coerce(sd)$X
invHodgeStar(g:SMR,x:DRC):DRC == x=0$DRC => x y:DRC:=leadingBasisTerm(x) k:X:=coerce(degree y)$X c:X:=s(g)*(-1)^(k*(coerce(n)$X-k)) leadingCoefficient(x)*hodgeStarBT(g, c*y) + _ invHodgeStar(g, reductum(x))
codifferential(g:SMR,x:DRC):DRC == x=0$DRC => 0 y:DRC:=leadingBasisTerm(x) k:X:=coerce(degree y)$X c:X:=s(g)*(-1)^(coerce(n)$X*(k-1)+1) c*hodgeStar(g, d hodgeStar(g, leadingCoefficient(x)*y)) + _ codifferential(g, reductum(x))
hodgeLaplacian(g:SMR,x:DRC):DRC == d codifferential(g, x)+ codifferential(g, d x)</spad>
fricas
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/7780364366861049302-25px001.spad
using old system compiler.
DFORM abbreviates package DifferentialForms
------------------------------------------------------------------------
initializing NRLIB DFORM for DifferentialForms
compiling into NRLIB DFORM
****** Domain: R already in scope
compiling local eab2li : ExtAlgBasis -> List Integer
DFORM;eab2li is replaced by x
Time: 0.01 SEC.
compiling local drc2rea : DeRhamComplex(R,
compiling exported d : DeRhamComplex(R,
compiling exported one : () -> DeRhamComplex(R,
compiling exported zero : () -> DeRhamComplex(R,
compiling exported baseForms : () -> List DeRhamComplex(R,
compiling exported coordVector : () -> List Expression R
Time: 0 SEC.
compiling exported coordSymbols : () -> List Symbol
Time: 0 SEC.
compiling exported vectorField : Symbol -> List Expression R
Time: 0 SEC.
compiling exported scalarField : Symbol -> Expression R
Time: 0 SEC.
compiling exported covectorField : Symbol -> List DeRhamComplex(R,
compiling exported zeroForm : Symbol -> DeRhamComplex(R,
compiling exported * : (List Expression R,
compiling exported * : (List DeRhamComplex(R,
compiling exported volumeForm : SquareMatrix(# v,
compiling exported monomials : NonNegativeInteger -> List DeRhamComplex(R,
compiling local flip : ExtAlgBasis -> ExtAlgBasis
Time: 0 SEC.
compiling local pos : (ExtAlgBasis,
compiling local dot1 : (SquareMatrix(# v,
compiling local dot2 : (SquareMatrix(# v,
compiling exported dot : (SquareMatrix(# v,
compiling exported proj : (NonNegativeInteger,
compiling exported conjBasisTerm : DeRhamComplex(R,
compiling exported atomizeBasisTerm : DeRhamComplex(R,
compiling local intProdBasisTerm : (Vector Expression R,
compiling exported interiorProduct : (Vector Expression R,
compiling exported lieDerivative : (Vector Expression R,
compiling local eps : DeRhamComplex(R,
compiling local hodgeStarBT : (SquareMatrix(# v,
compiling exported hodgeStar : (SquareMatrix(# v,
compiling exported s : SquareMatrix(# v,
compiling exported invHodgeStar : (SquareMatrix(# v,
compiling exported codifferential : (SquareMatrix(# v,
compiling exported hodgeLaplacian : (SquareMatrix(# v,
(time taken in buildFunctor: 0)
Time: 0 SEC.
Warnings:
[1] dot1: c has no value
[2] dot2: c has no value
[3] conjBasisTerm: k has no value
[4] atomizeBasisTerm: k has no value
[5] s: not known that (AlgebraicallyClosedField) is of mode (CATEGORY domain (IF (has R (IntegralDomain)) (PROGN (ATTRIBUTE (AlgebraicallyClosedFunctionSpace R)) (ATTRIBUTE (TranscendentalFunctionCategory)) (ATTRIBUTE (CombinatorialOpsCategory)) (ATTRIBUTE (LiouvillianFunctionCategory)) (ATTRIBUTE (SpecialFunctionCategory)) (SIGNATURE reduce (% %)) (SIGNATURE number? ((Boolean) %)) (IF (has R (PolynomialFactorizationExplicit)) (ATTRIBUTE (PolynomialFactorizationExplicit)) noBranch) (SIGNATURE setSimplifyDenomsFlag ((Boolean) (Boolean))) (SIGNATURE getSimplifyDenomsFlag ((Boolean)))) noBranch))
[6] s: not known that (TranscendentalFunctionCategory) is of mode (CATEGORY domain (IF (has R (IntegralDomain)) (PROGN (ATTRIBUTE (AlgebraicallyClosedFunctionSpace R)) (ATTRIBUTE (TranscendentalFunctionCategory)) (ATTRIBUTE (CombinatorialOpsCategory)) (ATTRIBUTE (LiouvillianFunctionCategory)) (ATTRIBUTE (SpecialFunctionCategory)) (SIGNATURE reduce (% %)) (SIGNATURE number? ((Boolean) %)) (IF (has R (PolynomialFactorizationExplicit)) (ATTRIBUTE (PolynomialFactorizationExplicit)) noBranch) (SIGNATURE setSimplifyDenomsFlag ((Boolean) (Boolean))) (SIGNATURE getSimplifyDenomsFlag ((Boolean)))) noBranch))
[7] s: not known that (FunctionSpace (Integer)) is of mode (CATEGORY domain (IF (has R (IntegralDomain)) (PROGN (ATTRIBUTE (AlgebraicallyClosedFunctionSpace R)) (ATTRIBUTE (TranscendentalFunctionCategory)) (ATTRIBUTE (CombinatorialOpsCategory)) (ATTRIBUTE (LiouvillianFunctionCategory)) (ATTRIBUTE (SpecialFunctionCategory)) (SIGNATURE reduce (% %)) (SIGNATURE number? ((Boolean) %)) (IF (has R (PolynomialFactorizationExplicit)) (ATTRIBUTE (PolynomialFactorizationExplicit)) noBranch) (SIGNATURE setSimplifyDenomsFlag ((Boolean) (Boolean))) (SIGNATURE getSimplifyDenomsFlag ((Boolean)))) noBranch))
[8] invHodgeStar: k is BOTH a variable and a literal
[9] invHodgeStar: c is BOTH a variable and a literal
[10] codifferential: k is BOTH a variable and a literal
[11] codifferential: c is BOTH a variable and a literal
Cumulative Statistics for Constructor DifferentialForms
Time: 1.25 seconds
finalizing NRLIB DFORM
Processing DifferentialForms for Browser database:
--------constructor---------
--------(* ((DeRhamComplex R v) (List (Expression R)) (List (DeRhamComplex R v))))---------
--------(* ((DeRhamComplex R v) (List (DeRhamComplex R v)) (List (DeRhamComplex R v))))---------
--------(d ((DeRhamComplex R v) (DeRhamComplex R v)))---------
--------(one ((DeRhamComplex R v)))---------
--------(zero ((DeRhamComplex R v)))---------
--------(baseForms ((List (DeRhamComplex R v))))---------
--------(coordVector ((List (Expression R))))---------
--------(coordSymbols ((List (Symbol))))---------
--------(vectorField ((List (Expression R)) (Symbol)))---------
--------(scalarField ((Expression R) (Symbol)))---------
--------(covectorField ((List (DeRhamComplex R v)) (Symbol)))---------
--------(zeroForm ((DeRhamComplex R v) (Symbol)))---------
--------(volumeForm ((DeRhamComplex R v) (SquareMatrix (# v) (Expression R))))---------
--------(conjBasisTerm ((DeRhamComplex R v) (DeRhamComplex R v)))---------
--->-->DifferentialForms((conjBasisTerm ((DeRhamComplex R v) (DeRhamComplex R v)))): Improper first word in comments: Return
"Return the complement of a basis term \\spad{w}.\\spad{r}.\\spad{t}. volumeForm"
--------(atomizeBasisTerm ((List (DeRhamComplex R v)) (DeRhamComplex R v)))---------
--->-->DifferentialForms((atomizeBasisTerm ((List (DeRhamComplex R v)) (DeRhamComplex R v)))): Improper first word in comments: Given
"Given a basis term,
; wrote /var/aw/var/LatexWiki/DFORM.NRLIB/DFORM.fasl
; compilation finished in 0:00:00.132
------------------------------------------------------------------------
DifferentialForms is now explicitly exposed in frame initial
DifferentialForms will be automatically loaded when needed from
/var/aw/var/LatexWiki/DFORM.NRLIB/DFORMTest flavours
- fricas
-- =======================================
- DFORM tests (package DifferentialForms)
-- =======================================
-- Requires:
-- .... DeRhamComplex (src/derham.spad) or FriCAS 1.3 or later.
-- .... DifferentialForms (dform.spad).
-- Version 1.1: 09-ARP-2016
-- Version 1.2: 17-DEC-2016
--
-- FriCAS Computer Algebra System
-- Version: FriCAS 1.3.0
-- Timestamp: Don Sep 29 21:26:01 CEST 2016
fricas
)set break resume
fricas)expose UnittestCount UnittestAux Unittest
UnittestCount is now explicitly exposed in frame initial UnittestAux is now explicitly exposed in frame initial Unittest is now explicitly exposed in frame initial
fricas)expose DFORM
DifferentialForms is already explicitly exposed in frame initial
----------------- testsuite "dform"
All user variables and function definitions have been cleared.Type: Voidfricastestcase "all"
All user variables and function definitions have been cleared.Type: Voidfricas-----------------
----------- -- Setup -- -----------
n:=7 -- dim of base space (n>=2 !),may change in course 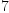
(1) Type: PositiveInteger?fricasN:=91 -- number of tests
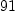
(2) Type: PositiveInteger?fricasO ==> OutputForm
Type: Voidfricas-- HodgeStar package for DERHAM(R,
v) R:=Integer -- Ring 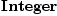
(3) Type: Typefricasv:=[subscript(x,
[j::OutputForm]) for j in 1..n] -- (x_1, .., x_n) ![\label{eq4}\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}\right]
\label{eq4}\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}\right]](images/6390044111034705366-16.0px.png)
(4) Type: List(Symbol)fricasM:=DFORM(R,
v) ![\label{eq5}\hbox{\axiomType{DifferentialForms}\ } \left({\hbox{\axiomType{Integer}\ } , \:{\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}\right]}}\right)
\label{eq5}\hbox{\axiomType{DifferentialForms}\ } \left({\hbox{\axiomType{Integer}\ } , \:{\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}\right]}}\right)](images/2960458786116569222-16.0px.png)
(5) Type: Typefricas-- basis 1-forms and coordinate vector dx:=baseForms()$M -- [dx[1],
..., dx[n]] ![\label{eq6}\left[{dx_{1}}, \:{dx_{2}}, \:{dx_{3}}, \:{dx_{4}}, \:{dx_{5}}, \:{dx_{6}}, \:{dx_{7}}\right]
\label{eq6}\left[{dx_{1}}, \:{dx_{2}}, \:{dx_{3}}, \:{dx_{4}}, \:{dx_{5}}, \:{dx_{6}}, \:{dx_{7}}\right]](images/4328433572927404047-16.0px.png)
(6) fricasx:=coordVector()$M -- [x[1],
..., x[n]] ![\label{eq7}\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}\right]
\label{eq7}\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}\right]](images/8913984492241947449-16.0px.png)
(7) Type: List(Expression(Integer))fricasxs:=coordSymbols()$M -- as above but as List Symbol (for differentiate,
D) ![\label{eq8}\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}\right]
\label{eq8}\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}\right]](images/796339507354631710-16.0px.png)
(8) Type: List(Symbol)fricas-- operator,
vector field, scalar field, symbol a:=operator 'a -- operator 
(9) Type: BasicOperator?fricasb:=vectorField(b)$M -- generic vector field [b1(x1..xn),
..., bn(x1..xn)] ![\label{eq10}\begin{array}{@{}l}
\displaystyle
\left[{{b_{1}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{b_{2}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{3}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{b_{4}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{5}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{b_{6}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{7}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}\right]
\label{eq10}\begin{array}{@{}l}
\displaystyle
\left[{{b_{1}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{b_{2}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{3}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{b_{4}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{5}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{b_{6}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{7}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}\right]](images/3493383917862598383-16.0px.png)
(10) Type: List(Expression(Integer))fricasc:=vectorField(c)$M
![\label{eq11}\begin{array}{@{}l}
\displaystyle
\left[{{c_{1}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{c_{2}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{c_{3}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{c_{4}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{c_{5}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{c_{6}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{c_{7}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}\right]
\label{eq11}\begin{array}{@{}l}
\displaystyle
\left[{{c_{1}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{c_{2}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{c_{3}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{c_{4}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{c_{5}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{c_{6}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{c_{7}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}\right]](images/7930435291298688763-16.0px.png)
(11) Type: List(Expression(Integer))fricasP:=scalarField(P)$M -- scalar field P(x1,
.., xn) 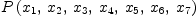
(12) Type: Expression(Integer)fricas-- (pseudo-) random form & zeroForm rd:=reduce(_*,
[dx.j for j in 1..random(n)$NNI+1]) 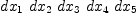
(13) fricasnf:=zeroForm(nf)$M
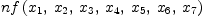
(14) fricas-- metric g:=diagonalMatrix([1 for i in 1..n])$SquareMatrix(n,
EXPR R) -- Euclidean 
(15) Type: SquareMatrix?(7,Expression(Integer)) fricash:=diagonalMatrix(c)$SquareMatrix(n,
EXPR R) 
(16) Type: SquareMatrix?(7,Expression(Integer)) fricas-- vector field vf:=vector b
![\label{eq17}\begin{array}{@{}l}
\displaystyle
\left[{{b_{1}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{b_{2}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{3}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{b_{4}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{5}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{b_{6}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{7}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}\right]
\label{eq17}\begin{array}{@{}l}
\displaystyle
\left[{{b_{1}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{b_{2}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{3}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{b_{4}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{5}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \:{{b_{6}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{7}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}, \:{x_{5}}, \:{x_{6}}, \:{x_{7}}}\right)}\right]](images/5826285831441545412-16.0px.png)
(17) Type: Vector(Expression(Integer))fricas-- Result list res:List(Boolean):=[false for j in 1..N]
![\label{eq18}\begin{array}{@{}l}
\displaystyle
\left[ \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} \right]
\label{eq18}\begin{array}{@{}l}
\displaystyle
\left[ \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \mbox{\rm false} , \: \right.
\
\
\displaystyle
\left. \mbox{\rm false} \right]](images/2524303185789024396-16.0px.png)
(18) Type: List(Boolean)fricas-- res.1 := test (dx.1=d(x.1*one()$M))
(19) Type: Booleanfricasres.2 := test (#dx = n)
(20) Type: Booleanfricasres.3 := test (#x = n)
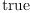
(21) Type: Booleanfricasres.4 := test (a x = a(x))
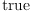
(22) Type: Booleanfricasres.5 := test (#b = n)
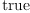
(23) Type: Booleanfricas-- null Form (i.e. degree 0) res.6 := test (zeroForm('a)$M = a(x)*one()$M)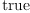
(24) Type: Booleanfricasres.7 := test (d zeroForm('a)$M = reduce(_+,[D(a(x), xs.i)*dx.i for i in 1..n])) 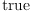
(25) Type: Booleanfricas-- products (à la Flanders,
vector forms) res.8 := test ( x*dx = reduce(_+, [x.i*dx.i for i in 1..n])) 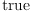
(26) Type: Booleanfricasres.9 := test ( dx * dx = 0)
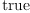
(27) Type: Booleanfricasres.10 := test ( (x*dx)*dx = -dx*(x*dx))
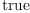
(28) Type: Booleanfricas-- (co-)vector field res.11 := test (vectorField(W)$M * dx = dx * vectorField(W)$M)
(29) Type: Booleanfricasres.12 := test (typeOf(vectorField(S)$M)::O=List(Expression(R))::O)
(30) Type: Booleanfricasres.13 := test (typeOf(covectorField(K)$M)::O=List(DERHAM(R,
v))::O) 
(31) Type: Booleanfricasres.14 := test (typeOf(vectorField(W)$M * covectorField(K)$M)::O=DERHAM(R,
v)::O) 
(32) Type: Booleanfricas-- dot products w.r.t. g res.15 := reduce(_and,
[test ( dot(g, dx.j, dx.j)$M = 1) for j in 1..n]) 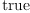
(33) Type: Booleanfricasres.16 := reduce(_and,
[test ( dot(g, dx.j, dx.(j+1))$M = 0) for j in 1..n-1]) 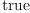
(34) Type: Booleanfricasres.17 := reduce(_and,
[test ( dot(g, dx.1*dx.j, dx.1*dx.j)$M = 1) for j in 2..n]) 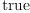
(35) Type: Booleanfricasres.18 := reduce(_and,
[test ( dot(h, dx.j, dx.j)$M = 1/c.j) for j in 1..n]) 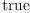
(36) Type: Booleanfricasres.19 := reduce(_and,
[test ( dot(h, dx.j, dx.(j+1))$M = 0) for j in 1..n-1]) 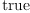
(37) Type: Booleanfricasres.20 := reduce(_and,
[test ( dot(h, dx.1*dx.j, dx.1*dx.j)$M = 1/(c.1*c.j)) _ for j in 2..n]) 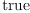
(38) Type: Booleanfricas-- Hodge star res.21 := test (one()$M*hodgeStar(g,
1)$M = dot(g, 1, 1)$M * volumeForm(g)$M) 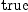
(39) Type: Booleanfricasres.22 := test (rd*hodgeStar(g,
rd)$M = dot(g, rd, rd)$M * volumeForm(g)$M) 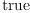
(40) Type: Booleanfricasres.23 := test (degree(hodgeStar(g,
dx.n)$M) = n-1) 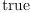
(41) Type: Booleanfricasres.24 := test (one()$M*hodgeStar(h,
1)$M = dot(h, 1, 1)$M * volumeForm(h)$M) 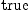
(42) Type: Booleanfricasres.25 := test (rd*hodgeStar(h,
rd)$M = dot(h, rd, rd)$M * volumeForm(h)$M) 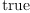
(43) Type: Booleanfricasres.26 := test (degree(hodgeStar(h,
dx.n)$M) = n-1) 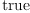
(44) Type: Booleanfricas-- Projections res.27 := test (proj(0,
nf+b*dx+d(b*dx))$M = nf) 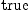
(45) Type: Booleanfricasres.28 := test (proj(1,
nf+b*dx+d(b*dx))$M = b*dx) 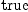
(46) Type: Booleanfricasres.29 := test (proj(2,
nf+b*dx+d(b*dx))$M = d(b*dx)) 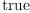
(47) Type: Booleanfricasres.30 := test (proj(n,
volumeForm(g)$M)$M = volumeForm(g)$M) 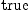
(48) Type: Booleanfricasres.31 := test (proj(random(n)$NNI,
volumeForm(g)$M)$M = 0) 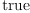
(49) Type: Booleanfricas-- Interior product res.32 := test (interiorProduct(vf,
dx.1)$M = b.1) 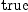
(50) Type: Booleanfricasres.33 := test (interiorProduct(vf,
dx.n)$M = b.n) 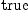
(51) Type: Booleanfricasres.34 := test (d interiorProduct(vf,
volumeForm(g)$M)$M = _ reduce(_+, [D(b.j, xs.j) for j in 1..n])*volumeForm(g)$M) 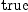
(52) Type: Booleanfricas-- Lie derivative res.35 := test ( d interiorProduct(vf,
b*dx)$M + _ interiorProduct(vf, d(b*dx))$M = lieDerivative(vf, b*dx)$M) 
(53) Type: Booleanfricas-- Version 1.2
fricas)clear values n R v M x xs dx a b c p g h P vf
n:=4 -- dim of base space (n>=2 !)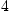
(54) Type: PositiveInteger?fricasO ==> OutputForm
Type: Voidfricas-- HodgeStar package for DERHAM(R,
v) R:=Integer -- Ring 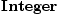
(55) Type: Typefricasv:=[subscript(x,
[j::OutputForm]) for j in 1..n] -- (x_1, .., x_n) ![\label{eq56}\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}\right]
\label{eq56}\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}\right]](images/3345471496839229848-16.0px.png)
(56) Type: List(Symbol)fricasM:=DFORM(R,
v) ![\label{eq57}\hbox{\axiomType{DifferentialForms}\ } \left({\hbox{\axiomType{Integer}\ } , \:{\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}\right]}}\right)
\label{eq57}\hbox{\axiomType{DifferentialForms}\ } \left({\hbox{\axiomType{Integer}\ } , \:{\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}\right]}}\right)](images/1769331272910471396-16.0px.png)
(57) Type: Typefricas-- basis 1-forms and coordinate vector dx:=baseForms()$M -- [dx[1],
..., dx[n]] ![\label{eq58}\left[{dx_{1}}, \:{dx_{2}}, \:{dx_{3}}, \:{dx_{4}}\right]
\label{eq58}\left[{dx_{1}}, \:{dx_{2}}, \:{dx_{3}}, \:{dx_{4}}\right]](images/3810655412312021350-16.0px.png)
(58) fricasx:=coordVector()$M -- [x[1],
..., x[n]] ![\label{eq59}\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}\right]
\label{eq59}\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}\right]](images/7593677555325692059-16.0px.png)
(59) Type: List(Expression(Integer))fricasxs:=coordSymbols()$M -- as above but as List Symbol (for differentiate,
D) ![\label{eq60}\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}\right]
\label{eq60}\left[{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}\right]](images/5612973322437648021-16.0px.png)
(60) Type: List(Symbol)fricas-- operator,
vector field, scalar field, symbol a:=operator 'a -- operator 
(61) Type: BasicOperator?fricasb:=vectorField(b)$M -- generic vector field [b1(x1..xn),
..., bn(x1..xn)] ![\label{eq62}\begin{array}{@{}l}
\displaystyle
\left[{{b_{1}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \:{{b_{2}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \:{{b_{3}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{4}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}\right]
\label{eq62}\begin{array}{@{}l}
\displaystyle
\left[{{b_{1}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \:{{b_{2}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \:{{b_{3}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{4}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}\right]](images/1827961830987664016-16.0px.png)
(62) Type: List(Expression(Integer))fricasc:=vectorField(c)$M
![\label{eq63}\begin{array}{@{}l}
\displaystyle
\left[{{c_{1}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \:{{c_{2}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \:{{c_{3}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{c_{4}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}\right]
\label{eq63}\begin{array}{@{}l}
\displaystyle
\left[{{c_{1}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \:{{c_{2}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \:{{c_{3}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{c_{4}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}\right]](images/5855587643410288639-16.0px.png)
(63) Type: List(Expression(Integer))fricasP:=scalarField(P)$M -- scalar field P(x1,
.., xn) 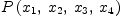
(64) Type: Expression(Integer)fricas-- metric g:=diagonalMatrix([1 for i in 1..n])$SquareMatrix(n,
EXPR R) -- Euclidean 
(65) Type: SquareMatrix?(4,Expression(Integer)) fricash:=diagonalMatrix(c)$SquareMatrix(n,
EXPR R) 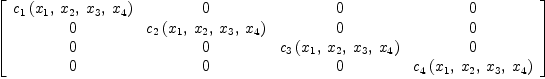
(66) Type: SquareMatrix?(4,Expression(Integer)) fricaseta:=diagonalMatrix(concat(1,
[-1 for i in 2..n]))$SquareMatrix(n, EXPR R) 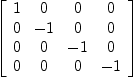
(67) Type: SquareMatrix?(4,Expression(Integer)) fricas-- vector field vf:=vector b
![\label{eq68}\begin{array}{@{}l}
\displaystyle
\left[{{b_{1}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \:{{b_{2}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \:{{b_{3}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{4}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}\right]
\label{eq68}\begin{array}{@{}l}
\displaystyle
\left[{{b_{1}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \:{{b_{2}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \:{{b_{3}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}, \: \right.
\
\
\displaystyle
\left.{{b_{4}}\left({{x_{1}}, \:{x_{2}}, \:{x_{3}}, \:{x_{4}}}\right)}\right]](images/2790231722787512946-16.0px.png)
(68) Type: Vector(Expression(Integer))fricas-- macros dV(g) ==> volumeForm(g)$M
Type: Voidfricasi(X,
w) ==> interiorProduct(X, w)$M Type: VoidfricasL(X,
w) ==> lieDerivative(X, w)$M Type: Voidfricas** w ==> hodgeStar(g,
w)$M Type: Voidfricas---
w:=x.1*dx.2-x.2*dx.1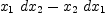
(69) fricasres.36 := test(d w = 2*dx.1*dx.2)
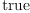
(70) Type: Booleanfricasres.37 := test(w*w = zero()$M)
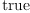
(71) Type: Booleanfricasres.38 := test(i(vf,
w) = x.1*b.2-x.2*b.1) 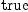
(72) Type: Booleanfricasres.39 := test(L(vf,
w) = d i(vf, w) + i(vf, d w)) 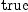
(73) Type: Booleanfricasres.40 := test(d i(vf,
w) + i(vf, d w) - L(vf, w) = zero()$M) 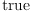
(74) Type: Booleanfricasres.41 := test(dot(g,
w, w)$M = x.1^2+x.2^2) 
(75) Type: Booleanfricas-- div(b) dV res.41 := test(d i(vf,
dV(g)) = reduce(_+, [D(b.j, xs.j) for j in 1..n])*dV(g)) 
(76) Type: Booleanfricasres.42 := test(d (P*one()$M) = reduce(_+,
[D(P, xs.j)*dx.j for j in 1..n])) 
(77) Type: Booleanfricasres.43 := test(i(vf,
d (P*one()$M))= reduce(_+, [D(P, xs.j)*b.j for j in 1..n])*one()$M) 
(78) Type: Booleanfricasres.44 := test(1/dot(g,
w, w)$M*w = w*(1/(x.1^2+x.2^2))) 
(79) Type: Booleanfricasres.45 := test(d (1/dot(g,
w, w)$M*w) = zero()$M) 
(80) Type: Booleanfricas--- s:=zeroForm('s)$M
(81) fricasres.46 := test(d s = totalDifferential(retract s)$DeRhamComplex(Integer,
v)) 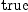
(82) Type: Booleanfricasres.47 := test(d s = totalDifferential(retract s)$typeOf(s))
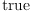
(83) Type: Booleanfricasres.48 := test(d (** s) = 0$typeOf(s))
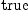
(84) Type: Booleanfricasres.49 := test(dot(g,
** ( d s), w*dx.2*dx.3)$M = x.2*D(retract s, xs.4)) 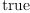
(85) Type: Booleanfricasres.50 := test(d (** ( d s)) = reduce(_+,
[D(retract s, xs.j, 2) for j in 1..n])*dV(g)) 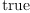
(86) Type: Booleanfricasr:=sin(x.1*x.2)*one()$M
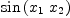
(87) fricasres.51 := test(d r = x.1*cos(x.1*x.2)*dx.2+x.2*cos(x.1*x.2)*dx.1)
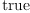
(88) Type: Booleanfricasres.52 := test(d (** ( d r)) = -(x.1^2+x.2^2)*sin(x.1*x.2)*dV(g))
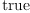
(89) Type: Booleanfricasres.53 := test(** (d (** ( d r))) = -(x.1^2+x.2^2)*sin(x.1*x.2))
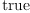
(90) Type: Booleanfricasres.53 := test(** (d (** ( d r)))::EXPR INT = retract (** (d (** ( d r)))))
(91) Type: Booleanfricasres.54 := test(eval(** (d (** ( d r)))::EXPR INT,
xs.1=%pi) = (-%pi^2-x.2^2)*sin(%pi*x.2)) 
(92) Type: Booleanfricasres.55 := test(eval(eval(** (d (** ( d r)))::EXPR INT,
xs.1=%pi) , xs.2=%pi)=-2*%pi^2*sin(%pi^2)) 
(93) Type: Booleanfricasa(P)*one()$M
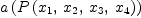
(94) fricas-- chain diff res.56 := test(d (a(P)*one()$M) = eval(D(a(t),
't), t=P)*d (P*one()$M)) 
(95) Type: Booleanfricasres.57 := test(** invHodgeStar(g,
w)$M = w) 
(96) Type: Booleanfricasres.58 := test(invHodgeStar(g,
** w)$M = w) 
(97) Type: Booleanfricasres.59 := test(** invHodgeStar(g,
** w + dx.1)$M = ** w + dx.1) 
(98) Type: Booleanfricasres.60 := test( ** dV(g) = invHodgeStar(g,
dV(g))$M) 
(99) Type: Booleanfricasres.61 := test(** dV(h) ~= invHodgeStar(h,
dV(g))$M) 
(100) Type: Booleanfricasres.62 := test( dot(h,
w, w)$M = (c.2*x.2^2+c.1*x.1^2)/(c.1*c.2)) 
(101) Type: Booleanfricasres.63 := test( s(g)$M = 1)
(102) Type: Booleanfricasres.64 := test( s(eta)$M = -1)
(103) Type: Booleanfricasres.65 := test( s(h)$M = 's? )
(104) Type: Booleanfricas-- https://en.wikipedia.org/wiki/Hodge_dual -- Four dimensions
res.66 := test( hodgeStar(eta,dx.1)$M = dx.2*dx.3*dx.4) 
(105) Type: Booleanfricasres.67 := test( hodgeStar(eta,
dx.2)$M = dx.1*dx.3*dx.4) 
(106) Type: Booleanfricasres.68 := test( hodgeStar(eta,
dx.3)$M = dx.1*dx.4*dx.2) 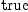
(107) Type: Booleanfricasres.69 := test( hodgeStar(eta,
dx.4)$M = dx.1*dx.2*dx.3) 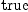
(108) Type: Booleanfricasres.70 := test( hodgeStar(eta,
dx.1*dx.2)$M = dx.4*dx.3) 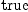
(109) Type: Booleanfricasres.71 := test( hodgeStar(eta,
dx.1*dx.3)$M = dx.2*dx.4) 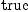
(110) Type: Booleanfricasres.72 := test( hodgeStar(eta,
dx.1*dx.4)$M = dx.3*dx.2) 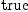
(111) Type: Booleanfricasres.73 := test( hodgeStar(eta,
dx.2*dx.3)$M = dx.1*dx.4) 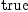
(112) Type: Booleanfricasres.74 := test( hodgeStar(eta,
dx.2*dx.4)$M = dx.3*dx.1) 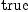
(113) Type: Booleanfricasres.75 := test( hodgeStar(eta,
dx.3*dx.4)$M = dx.1*dx.2) 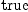
(114) Type: Booleanfricas-- codifferential: (delta=(-)^degree(x)*invHodgeStar(g,
d hodgeStar(g, x)) res.76 := test(codifferential(g, s*dx.1)$M = -D(retract s, xs.1)*one()$M) 
(115) Type: Booleanfricasres.77 := test(codifferential(g,
P*dx.2)$M = -D(P, xs.2)*one()$M) 
(116) Type: Booleanfricasres.78 := test(codifferential(g,
s*P*dx.1*dx.2)$M = _ (-P*D(retract s, xs.1)-s*D(P, xs.1))*dx.2+_ (P*D(retract s, xs.2)+s*D(P, xs.2))*dx.1) 
(117) Type: Booleanfricasres.79 := test(codifferential(g,
P*w)$M = x.2*D(P, xs.1)*one()$M -_ x.1*D(P, xs.2)*one()$M) 
(118) Type: Booleanfricasres.80 := test(codifferential(g,
P*w)$M = _ (-1)^degree(w)*invHodgeStar(g, d hodgeStar(g, P*w)$M)$M) 
(119) Type: Booleanfricasres.81 := test(codifferential(eta,
P*w)$M = _ (-1)^degree(w)*invHodgeStar(eta, d hodgeStar(eta, P*w)$M)$M) 
(120) Type: Booleanfricasres.82 := test(codifferential(h,
P*w)$M = _ (-1)^degree(w)*invHodgeStar(h, d hodgeStar(h, P*w)$M)$M) 
(121) Type: Booleanfricasres.83 := test(codifferential(h,
P*w*dx.3)$M = _ (-1)^degree(w*dx.3)*invHodgeStar(h, d hodgeStar(h, P*w*dx.3)$M)$M) 
(122) Type: Booleanfricas-- the codifferential \delta is (sort of) the adjoint to the differential. -- This doesn’t quite hold,
but we can show that it does hold “up to homology”. -- We can calculate their difference times the canonical volume form: res.84 := test((dot(g, d w, dx.1*dx.2)$M -_ dot(g, w, codifferential(g, dx.1*dx.2)$M)$M)*dV(g)= d (w*hodgeStar(g, dx.1*dx.2)$M)) 
(123) Type: Booleanfricasres.85 := test((dot(eta,
d w, dx.1*dx.2)$M -_ dot(eta, w, codifferential(eta, dx.1*dx.2)$M)$M)*dV(eta)= d (w*hodgeStar(eta, dx.1*dx.2)$M)) 
(124) Type: Booleanfricasres.86 := test(hodgeLaplacian(g,
w*(** w))$M = -4 * dV(g)) 
(125) Type: Booleanfricasres.87 := test(hodgeLaplacian(eta,
w*(hodgeStar(eta, w)$M))$M = 4 * dV(eta)) 
(126) Type: Booleanfricasres.88 := test(hodgeLaplacian(h,
w*(hodgeStar(h, w)$M))$M =_ d codifferential(h, w*hodgeStar(h, w)$M)$M) 
(127) Type: Booleanfricasres.89 := test(d(vf*dx) * (** d(vf*dx))=dot(g,
d(vf*dx), d(vf*dx))$M*dV(g)) 
(128) Type: Booleanfricas-- next is inequality because ** = hodgeStar w.r.t to metric g! res.90 := test(d(vf*dx) * (** d(vf*dx))~=dot(eta,
d(vf*dx), d(vf*dx))$M*dV(eta)) 
(129) Type: Booleanfricas-- correct is: res.91 := test(d(vf*dx)*hodgeStar(eta,
d(vf*dx))$M=_ dot(eta, d(vf*dx), d(vf*dx))$M*dV(eta)) 
(130) Type: Booleanfricas------------- -- Results -- -------------
fricas)version
"FriCAS 1.3.12 compiled at Sat 7 Jun 23:54:49 CEST 2025"fricas)lisp (lisp-implementation-type)
Your user access level is compiler and this command is therefore not available. See the )set userlevel command for more information.fricas)lisp (lisp-implementation-version)
Your user access level is compiler and this command is therefore not available. See the )set userlevel command for more information.
res![\label{eq131}\begin{array}{@{}l}
\displaystyle
\left[ \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} \right]
\label{eq131}\begin{array}{@{}l}
\displaystyle
\left[ \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} , \right.
\
\
\displaystyle
\left.\: \mbox{\rm true} , \: \mbox{\rm true} , \: \mbox{\rm true} \right]](images/8650955838875943290-16.0px.png)
(131) Type: List(Boolean)fricasreduce(_and,
res) 
(132) Type: Booleanfricas-- dummy statistics [testEquals("res." string(j),"true") for j in 1..N]; Type: List(Void)fricasstatistics()
============================================================================= General WARNINGS: * do not use ')clear completely' before having used 'statistics()' It clears the statistics without warning! * do not forget to pass the arguments of the testXxxx functions as Strings! Otherwise,the test will fail and statistics() will not notice!
============================================================================= Testsuite: dform failed (total): 0 (1)
============================================================================= testsuite | testcases: failed (total) | tests: failed (total) dform 0 (1) 0 (91) ============================================================================= File summary. unexpected failures: 0 expected failures: 0 unexpected passes: 0 total tests: 91Type: Void
Some changes necessary: use vectors instead of lists, ...