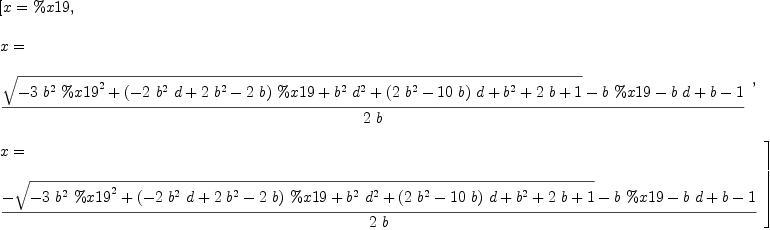fricas (1) -> )set output tex on fricas )set output algebra off fricas )set output mathml off Indefinite intregral arctan = atan fricas integrate(1/atan(x),
Type: Union(Expression(Integer),
Definite intregral fricas integrate(1/(a+z^3),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas integrate(a/(b+z^2),
Type: Union(f2: List(OrderedCompletion?(Expression(Integer))),
Solutions of Transcendental Equations fricas solve(cos(x)-y=-sin(x),
Type: List(Equation(Expression(Integer)))
fricas solve(cos(x)-y=-sin(x),
Type: List(Equation(Expression(Integer)))
fricas solve(cos(x)-y=-sin(x),
Type: List(Equation(Expression(Integer)))
fricas solve(cos(x)=0,
Type: List(Equation(Expression(Integer)))
fricas solve(sin(e) - e = 0,
Type: List(Equation(Expression(Integer)))
fricas solve(a*cos(t1) + b*sin(t1) = c,
Type: List(Equation(Expression(Integer)))
fricas solve(cos(x)-y=-sin(x),
Type: List(Equation(Expression(Integer)))
Matrices fricas A:=matrix[[cos(x)-y,
Type: Matrix(Expression(Integer))
There is no matrix solve: fricas solve(A=0, fricas A:=matrix[[cos(x)-L,
Type: Matrix(Expression(Integer))
fricas B:=solve(A(1,
Type: List(Equation(Expression(Integer)))
fricas B(1)
Type: Equation(Expression(Integer))
fricas A:=matrix[[cos(x)-L,
Type: Matrix(Expression(Integer))
fricas B=solve(A(1,
Type: Equation(List(Equation(Expression(Integer))))
fricas B(1)
Type: Equation(Expression(Integer))
fricas v:=vector[v11,
Type: Vector(OrderedVariableList([v11,
fricas v:=matrix[[B.1],
Type: Matrix(Equation(Expression(Integer)))
fricas [a,
Type: List(Equation(Expression(Integer)))
fricas a
Type: Equation(Expression(Integer))
fricas b
Type: Equation(Expression(Integer))
fricas LA1:=[sqrt(-1)*sin(x)+cos(x),
Type: List(Expression(Integer))
fricas LA1:=matrix[[sqrt(-1)*sin(x)+cos(x),
Type: Matrix(Expression(Integer))
Complex Values fricas LA1:=matrix[[sqrt(-1)*sin(x)]]
Type: Matrix(Expression(Integer))
fricas A:=matrix[[cos(x)-L]]
Type: Matrix(Expression(Integer))
Due to mismatched type the following produces scripted symbol! fricas A:=matrix[a,
Type: Symbol
fricas A:=matrix[[a,
Type: Matrix(Equation(Expression(Integer)))
fricas A:=matrix[[a],
Type: Matrix(Equation(Expression(Integer)))
Again, due to mismatched types we get scripted symbol! fricas A:=matrix[[sqrt(-1)*sin(x)+cos(x)],
Type: Symbol
fricas A:=matrix[[sqrt(-1)*sin(x)+cos(x)],
Type: Matrix(Expression(Integer))
fricas LA1:=matrix[[sqrt(-1)*sin(x)+cos(x)],
Type: Matrix(Expression(Integer))
fricas LAM:=matrix[[sqrt(-1)*sin(x)+cos(x)],
Type: Matrix(Expression(Integer))
fricas A:=matrix[[cos(x)-L,
Type: Matrix(Expression(Integer))
fricas D:=matrix[[sqrt(-1)*sin(x)+cos(x)],
Type: Matrix(Expression(Integer))
fricas A*D
Type: Matrix(Expression(Integer))
fricas v:=matrix[[v11],
Type: Matrix(Polynomial(Integer))
fricas A*v
Type: Matrix(Expression(Integer))
fricas D(1,
Type: Matrix(Expression(Integer))
fricas solve([w = 0 for w in parts(A*v - D(1,
Type: List(List(Equation(Expression(Integer))))
Note that the following does not work: fricas solve(A*vA*v=D(1, despite possibility of creating matrix equations: fricas A*vA*v=D(1,
Type: Equation(Matrix(Expression(Integer)))
Undetermined example: fricas A:=matrix[[cos(x),
Type: Matrix(Expression(Integer))
fricas D:=matrix[[sqrt(-1)*sin(x)+cos(x)],
Type: Matrix(Expression(Integer))
fricas v:=matrix[[v11],
Type: Matrix(Polynomial(Integer))
fricas A*v
Type: Matrix(Expression(Integer))
fricas D(1,
Type: Matrix(Expression(Integer))
fricas A*v-D(1,
Type: Matrix(Expression(Integer))
fricas solve([w = 0 for w in parts(A*v-D(1,
Type: List(List(Equation(Expression(Integer))))
fricas A:=matrix[[cos(x),
Type: Matrix(Expression(Integer))
Differential Equations fricas )clear all
Type: BasicOperator?
fricas solve(D(y x, fricas deq := (x^2 + 1) * D(y x,
Type: Equation(Expression(Integer))
fricas solve(deq,
Type: Union(Record(particular: Expression(Integer),
fricas solve(D(y(x),
Type: Union(Expression(Integer),
Just trying to understand the syntax fricas solve(a*x^2+b*x+c,
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas solve(a*x^2+b*x+c=0,
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas zerosOf(a*x^2+b*x+c,
Type: List(Expression(Integer))
fricas zerosOf(sqrt(h^2+a^2)-a=d, fricas solve(x^2+x+1=98,
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas solve(x^2+2*x+1=0,
Type: List(Equation(Fraction(Polynomial(Integer))))
Solutions in Expression domain fricas solve((x^2+x+1=98)::Equation Expression Integer,
Type: List(Equation(Expression(Integer)))
fricas solve((x^3 * b + x^2*(b*d - b + 1) + x*(3*d - b*d - 1) + 2*d^2 - 2*d = 0)::Equation Expression Integer,
Type: List(Equation(Expression(Integer)))
|
|
|
|
last edited 8 years ago by test1 |

![\label{eq3}\begin{array}{@{}l}
\displaystyle
\left[{\frac{{a \ {\log \left({\frac{{{\left(-{4 \ {{b}^{2}}}+{4 \ b}\right)}\ {\sqrt{- b}}}-{{b}^{3}}+{6 \ {{b}^{2}}}- b}{{{b}^{2}}+{2 \ b}+ 1}}\right)}}-{a \ {\log \left({- b}\right)}}}{4 \ {\sqrt{- b}}}}, \right.
\
\
\displaystyle
\left.\:{\frac{a \ {\arctan \left({\frac{\sqrt{b}}{b}}\right)}}{\sqrt{b}}}\right]
\label{eq3}\begin{array}{@{}l}
\displaystyle
\left[{\frac{{a \ {\log \left({\frac{{{\left(-{4 \ {{b}^{2}}}+{4 \ b}\right)}\ {\sqrt{- b}}}-{{b}^{3}}+{6 \ {{b}^{2}}}- b}{{{b}^{2}}+{2 \ b}+ 1}}\right)}}-{a \ {\log \left({- b}\right)}}}{4 \ {\sqrt{- b}}}}, \right.
\
\
\displaystyle
\left.\:{\frac{a \ {\arctan \left({\frac{\sqrt{b}}{b}}\right)}}{\sqrt{b}}}\right]](images/2485017816368834866-16.0px.png)
![\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{x ={2 \ {\arctan \left({\frac{{\sqrt{-{{y}^{2}}+ 2}}+ 1}{y + 1}}\right)}}}, \: \right.
\
\
\displaystyle
\left.{x = -{2 \ {\arctan \left({\frac{{\sqrt{-{{y}^{2}}+ 2}}- 1}{y + 1}}\right)}}}\right]
\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{x ={2 \ {\arctan \left({\frac{{\sqrt{-{{y}^{2}}+ 2}}+ 1}{y + 1}}\right)}}}, \: \right.
\
\
\displaystyle
\left.{x = -{2 \ {\arctan \left({\frac{{\sqrt{-{{y}^{2}}+ 2}}- 1}{y + 1}}\right)}}}\right]](images/3884206646919035133-16.0px.png)
![\label{eq6}\begin{array}{@{}l}
\displaystyle
\left[{x ={2 \ {\arctan \left({\frac{{\sqrt{-{{y}^{2}}+ 2}}+ 1}{y + 1}}\right)}}}, \: \right.
\
\
\displaystyle
\left.{x = -{2 \ {\arctan \left({\frac{{\sqrt{-{{y}^{2}}+ 2}}- 1}{y + 1}}\right)}}}\right]
\label{eq6}\begin{array}{@{}l}
\displaystyle
\left[{x ={2 \ {\arctan \left({\frac{{\sqrt{-{{y}^{2}}+ 2}}+ 1}{y + 1}}\right)}}}, \: \right.
\
\
\displaystyle
\left.{x = -{2 \ {\arctan \left({\frac{{\sqrt{-{{y}^{2}}+ 2}}- 1}{y + 1}}\right)}}}\right]](images/2178648806848130815-16.0px.png)
![\label{eq9}\begin{array}{@{}l}
\displaystyle
\left[{t 1 ={2 \ {\arctan \left({\frac{{\sqrt{-{{c}^{2}}+{{b}^{2}}+{{a}^{2}}}}+ b}{c + a}}\right)}}}, \: \right.
\
\
\displaystyle
\left.{t 1 = -{2 \ {\arctan \left({\frac{{\sqrt{-{{c}^{2}}+{{b}^{2}}+{{a}^{2}}}}- b}{c + a}}\right)}}}\right]
\label{eq9}\begin{array}{@{}l}
\displaystyle
\left[{t 1 ={2 \ {\arctan \left({\frac{{\sqrt{-{{c}^{2}}+{{b}^{2}}+{{a}^{2}}}}+ b}{c + a}}\right)}}}, \: \right.
\
\
\displaystyle
\left.{t 1 = -{2 \ {\arctan \left({\frac{{\sqrt{-{{c}^{2}}+{{b}^{2}}+{{a}^{2}}}}- b}{c + a}}\right)}}}\right]](images/565288248488848082-16.0px.png)
![\label{eq10}\begin{array}{@{}l}
\displaystyle
\left[{x ={2 \ {\arctan \left({\frac{{\sqrt{-{{y}^{2}}+ 2}}+ 1}{y + 1}}\right)}}}, \: \right.
\
\
\displaystyle
\left.{x = -{2 \ {\arctan \left({\frac{{\sqrt{-{{y}^{2}}+ 2}}- 1}{y + 1}}\right)}}}\right]
\label{eq10}\begin{array}{@{}l}
\displaystyle
\left[{x ={2 \ {\arctan \left({\frac{{\sqrt{-{{y}^{2}}+ 2}}+ 1}{y + 1}}\right)}}}, \: \right.
\
\
\displaystyle
\left.{x = -{2 \ {\arctan \left({\frac{{\sqrt{-{{y}^{2}}+ 2}}- 1}{y + 1}}\right)}}}\right]](images/5901935452784818497-16.0px.png)
![\label{eq16}\begin{array}{@{}l}
\displaystyle
{\left[{L ={{{\sqrt{- 1}}\ {\sin \left({x}\right)}}+{\cos \left({x}\right)}}}, \:{L ={-{{\sqrt{- 1}}\ {\sin \left({x}\right)}}+{\cos \left({x}\right)}}}\right]}= \
\
\displaystyle
{\left[{L ={{{\sqrt{- 1}}\ {\sin \left({x}\right)}}+{\cos \left({x}\right)}}}, \:{L ={-{{\sqrt{- 1}}\ {\sin \left({x}\right)}}+{\cos \left({x}\right)}}}\right]}
\label{eq16}\begin{array}{@{}l}
\displaystyle
{\left[{L ={{{\sqrt{- 1}}\ {\sin \left({x}\right)}}+{\cos \left({x}\right)}}}, \:{L ={-{{\sqrt{- 1}}\ {\sin \left({x}\right)}}+{\cos \left({x}\right)}}}\right]}= \
\
\displaystyle
{\left[{L ={{{\sqrt{- 1}}\ {\sin \left({x}\right)}}+{\cos \left({x}\right)}}}, \:{L ={-{{\sqrt{- 1}}\ {\sin \left({x}\right)}}+{\cos \left({x}\right)}}}\right]}](images/2051760077061943340-16.0px.png)
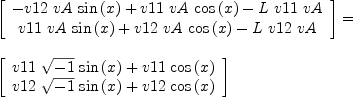
![\label{eq52}\begin{array}{@{}l}
\displaystyle
\left[{particular = 0}, \: \right.
\
\
\displaystyle
\left.{basis ={\left[{\frac{1}{\sqrt{{{x}^{2}}+ 1}}}, \:{\frac{\log \left({{\sqrt{{{x}^{2}}+ 1}}- x}\right)}{\sqrt{{{x}^{2}}+ 1}}}\right]}}\right]
\label{eq52}\begin{array}{@{}l}
\displaystyle
\left[{particular = 0}, \: \right.
\
\
\displaystyle
\left.{basis ={\left[{\frac{1}{\sqrt{{{x}^{2}}+ 1}}}, \:{\frac{\log \left({{\sqrt{{{x}^{2}}+ 1}}- x}\right)}{\sqrt{{{x}^{2}}+ 1}}}\right]}}\right]](images/1092109460797025680-16.0px.png)
![\label{eq59}\left[{x ={\frac{{\sqrt{389}}- 1}{2}}}, \:{x ={\frac{-{\sqrt{3
89}}- 1}{2}}}\right]
\label{eq59}\left[{x ={\frac{{\sqrt{389}}- 1}{2}}}, \:{x ={\frac{-{\sqrt{3
89}}- 1}{2}}}\right]](images/2447331125944112638-16.0px.png)