|
|
|
last edited 2 years ago by test1 |
Edit detail for RandomAlgebra revision 1 of 3
| 1 2 3 | ||
|
Editor: 127.0.0.1
Time: 2007/11/11 11:24:19 GMT-8 |
||
| Note: transferred from axiom-developer | ||
changed: - (the maths inside is not meant to be taken seriously; 'tis a silly idea that can't work) *from a recent email by Peter Broadbery* Random variables are assumed to have the following properties: 1. complex constants are random variables; 2. the sum of two random variables is a random variable; 3. the product of two random variables is a random variable; 4. addition and multiplication of random variables are both commutative; and 5. there is a notion of conjugation of random variables, satisfying: $(ab)* = b* a*$ and $a** = a$ for all random variables $a$, $b$, and coinciding with complex conjugation if $a$ is a constant. This means that random variables form complex abelian $*$-algebras. If $a = a*$, the random variable a is called "real". An expectation E on an algebra A of random variables is a normalized, positive linear functional. What this means is that 1. $E(1) = 1$; 2. $E(a * a) >= 0$ for all random variables $a$; 3. $E(a + b) = E(a) + E(b)$ for all random variables $a$ and $b$; and 4. $E(za) = zE(a)$ if $z$ is a constant. $*$-algebra *From Wikipedia, the free encyclopedia* In mathematics, a $*$-algebra is an associative algebra over the field of complex numbers with an antilinear, antiautomorphism $* : A \rightarrow A$ which is an involution. More precisely, $*$ is required to satisfy the following properties: * $(x + y)^* = x^* + y^* \quad $ * $(z x)^* = \overline{z} x^* $ * $(x y)^* = y^* x^* \quad $ * $(x^*)^* = x \quad $ for all $x$,$y$ in $A$, and all $z$ in $C$. The most obvious example of a $*$-algebra is the field of complex numbers C where $*$ is just complex conjugation. Another example is the algebra of nn matrices over $C$ with $*$ given by the conjugate transpose. An algebra homomorphism $f : A \rightarrow B$ is a $*$-homomorphism if it is compatible with the involutions of $A$ and $B$, i.e. * $f(a * ) = f(a) *$ for all $a$ in $A$. An element $a$ in $A$ is called self-adjoint if $a* = a$. \begin{aldor} #include "axiom" RandomAlgebra(F: Field): Category == with { Algebra F; E: % -> F; sample: % -> F; } local PolyHelper(F: Field): with { expand: SparseUnivariatePolynomial F -> Generator Cross(F, NonNegativeInteger); } == add { expand(p: SparseUnivariatePolynomial F): Generator Cross(F, NonNegativeInteger) == generate { default m: SparseUnivariatePolynomial F; import from SparseUnivariatePolynomial F; import from List SparseUnivariatePolynomial F; for m in monomials p repeat { yield (leadingCoefficient m, degree m); } } } UnivariateNormalRandomAlgebra: RandomAlgebra Float with { X: () -> %; variance: % -> Float; } == add { Rep ==> SparseUnivariatePolynomial Float; import from Rep; 0: % == per 0; 1: % == per 1; X(): % == per(monomial(1$Float,1$NonNegativeInteger)$Rep); characteristic(): NonNegativeInteger == 0; -(x: %): % == per(-rep x); (a: %) = (b: %): Boolean == rep(a) = rep(b); (a: %) + (b: %): % == per(rep(a) + rep(b)); (a: %) * (b: %): % == per(rep(a) * rep(b)); (a: Float) * (b: %): % == per(a * rep(b)); coerce(x: Integer): % == per(x::Rep); coerce(x: Float): % == per(x::Rep); coerce(x: %): OutputForm == coerce rep(x); E(X: %): Float == { import from PolyHelper Float; z: Float := 0; for p in expand rep(X) repeat { (a, b) := p; z := z + a * E(b); } z } -- should be a random sampling of x. sample(X: %): Float == { import from PolyHelper Float; import from Float; u := uniform01()$RandomFloatDistributions; x: Float := 0; for p in expand rep(X) repeat { (a, b) := p; x := x + a * u^b; } return x; } variance(X: %): Float == { A := (X-E(X)*1); E(A*A); } -- return expected value of X^n local E(n: NonNegativeInteger): Float == { p: Rep := 1; -- yuck. There must be a nicer way than this.. for i in 1..n repeat p := differentiate(p) + monomial(1,1)*p; coefficient(p,0); } } \end{aldor} \begin{axiom} a := X()$UnivariateNormalRandomAlgebra -- a number, normally distributed sample a -- 0 E a -- 1 variance(a) -- 1 variance(a+5) -- 5 variance(a+5) -- 3, apparently variance(a^2 + a) \end{axiom}
(the maths inside is not meant to be taken seriously; 'tis a silly idea that can't work)
from a recent email by Peter Broadbery
Random variables are assumed to have the following properties:
- complex constants are random variables;
- the sum of two random variables is a random variable;
- the product of two random variables is a random variable;
- addition and multiplication of random variables are both commutative; and
- there is a notion of conjugation of random variables, satisfying:
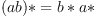 and
and 
for all random variables
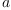 ,
, 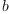 , and coinciding with complex conjugation
if
, and coinciding with complex conjugation
if 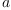 is a constant.
is a constant.
This means that random variables form complex abelian ![]() -algebras. If
-algebras. If ![]() ,
the random variable a is called "real".
,
the random variable a is called "real".
An expectation E on an algebra A of random variables is a normalized, positive linear functional. What this means is that
-
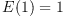 ;
; -
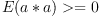 for all random variables
for all random variables  ;
; -
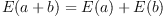 for all random variables
for all random variables 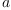 and
and 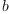 ; and
; and -
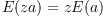 if
if 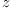 is a constant.
is a constant.
 -algebra
-algebra
From Wikipedia, the free encyclopedia
In mathematics, a ![]() -algebra is an associative algebra over the field of
complex numbers with an antilinear, antiautomorphism
-algebra is an associative algebra over the field of
complex numbers with an antilinear, antiautomorphism ![]() which is an
involution. More precisely,
which is an
involution. More precisely, ![]() is required to satisfy the following properties:
is required to satisfy the following properties:
for all ![]() ,
,![]() in
in ![]() , and all
, and all ![]() in
in ![]() .
.
The most obvious example of a ![]() -algebra is the field of complex numbers C
where
-algebra is the field of complex numbers C
where ![]() is just complex conjugation. Another example is the algebra of nn
matrices over
is just complex conjugation. Another example is the algebra of nn
matrices over ![]() with
with ![]() given by the conjugate transpose.
given by the conjugate transpose.
An algebra homomorphism ![]() is a
is a ![]() -homomorphism if it is compatible
with the involutions of
-homomorphism if it is compatible
with the involutions of ![]() and
and ![]() , i.e.
, i.e.
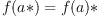 for all
for all 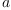 in
in 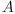 .
.
An element ![]() in
in ![]() is called self-adjoint if
is called self-adjoint if ![]() .
.
#include "axiom"
RandomAlgebra(F: Field): Category == with { Algebra F; E: % -> F; sample: % -> F; }
local PolyHelper(F: Field): with { expand: SparseUnivariatePolynomial F -> Generator Cross(F,NonNegativeInteger); } == add { expand(p: SparseUnivariatePolynomial F): Generator Cross(F, NonNegativeInteger) == generate { default m: SparseUnivariatePolynomial F; import from SparseUnivariatePolynomial F; import from List SparseUnivariatePolynomial F; for m in monomials p repeat { yield (leadingCoefficient m, degree m); } } }
UnivariateNormalRandomAlgebra: RandomAlgebra Float with { X: () -> %; variance: % -> Float; } == add { Rep ==> SparseUnivariatePolynomial Float; import from Rep;
0: % == per 0; 1: % == per 1; X(): % == per(monomial(1$Float,1$NonNegativeInteger)$Rep);
characteristic(): NonNegativeInteger == 0;
-(x: %): % == per(-rep x); (a: %) = (b: %): Boolean == rep(a) = rep(b);
(a: %) + (b: %): % == per(rep(a) + rep(b)); (a: %) * (b: %): % == per(rep(a) * rep(b)); (a: Float) * (b: %): % == per(a * rep(b));
coerce(x: Integer): % == per(x::Rep); coerce(x: Float): % == per(x::Rep);
coerce(x: %): OutputForm == coerce rep(x);
E(X: %): Float == { import from PolyHelper Float; z: Float := 0; for p in expand rep(X) repeat { (a,b) := p; z := z + a * E(b); } z }
-- should be a random sampling of x. sample(X: %): Float == { import from PolyHelper Float; import from Float; u := uniform01()$RandomFloatDistributions; x: Float := 0; for p in expand rep(X) repeat { (a,b) := p; x := x + a * u^b; } return x; }
variance(X: %): Float == { A := (X-E(X)*1); E(A*A); }
-- return expected value of X^n local E(n: NonNegativeInteger): Float == { p: Rep := 1; -- yuck. There must be a nicer way than this.. for i in 1..n repeat p := differentiate(p) + monomial(1,1)*p; coefficient(p, 0); } }
Compiling FriCAS source code from file
/var/zope2/var/LatexWiki/2618023199496535153-25px001.as using
AXIOM-XL compiler and options
-O -Fasy -Fao -Flsp -laxiom -Mno-ALDOR_W_WillObsolete -DAxiom -Y $AXIOM/algebra -I $AXIOM/algebra
Use the system command )set compiler args to change these
options.
Compiling Lisp source code from file
./2618023199496535153-25px001.lsp
Issuing )library command for 2618023199496535153-25px001
Reading /var/zope2/var/LatexWiki/2618023199496535153-25px001.asy
RandomAlgebra is now explicitly exposed in frame initial
RandomAlgebra will be automatically loaded when needed from
/var/zope2/var/LatexWiki/2618023199496535153-25px001
UnivariateNormalRandomAlgebra is now explicitly exposed in frame
initial
UnivariateNormalRandomAlgebra will be automatically loaded when
needed from /var/zope2/var/LatexWiki/2618023199496535153-25px001
>> System error:
The bounding indices 163 and 162 are bad for a sequence of length 162.
See also:
The ANSI Standard,a := X()$UnivariateNormalRandomAlgebra
| (1) |
-- a number,normally distributed sample a
| (2) |
-- 0 E a
| (3) |
-- 1 variance(a)
| (4) |
-- 1 variance(a+5)
| (5) |
-- 5 variance(a+5)
| (6) |
-- 3,apparently variance(a^2 + a)
| (7) |