|
|
|
last edited 11 years ago by page |
Edit detail for Jet LUDecomposition revision 3 of 3
| 1 2 3 | ||
|
Editor: page
Time: 2013/03/21 21:14:06 GMT+0 |
||
| Note: | ||
removed: -\begin{spad} -)abb package LUD LUDecomposition - -Sy ==> Symbol -L ==> List -V ==> Vector -VD ==> Vector D -MD ==> Matrix D -FD ==> Fraction D -MFD ==> Matrix FD -I ==> Integer -NNI ==> NonNegativeInteger -B ==> Boolean -OUT ==> OutputForm - -ROWREC ==> Record(Indices:L C, Entries:L D) - -iter ==> "iterated"::Sy -rand ==> "random"::Sy - -++ Description: -++ \axiomType{LUDecomposition} contains procedures to solve linear systems of -++ equations or to compute inverses using a LU decomposition. - -LUDecomposition(D:Field) : Cat == Def where - - Cat ==> with - - LUDecomp : MD -> Record(LU:MD, Perm:V I, Pivots:L D) - ++ \axiom{LUDecomp(A)} computes a LU decomposition of \axiom{A} - ++ using the algorithm of Crout. \axiom{LU} contains both triangular - ++ matrices; \axiom{Perm} is the permutation used for partial - ++ pivoting and \axiom{Pivots} yields the used pivots. - - LUSolve : (MD, V I, V D) -> V D - ++ \axiom{LUSolve(LU,Perm,B)} uses a previously computed LU - ++ decomposition to solve a linear system with right hand side - ++ \axiom{B}. \axiom{LU} and \axiom{Perm} are as given by - ++ \axiom{LUDecomp}. - - LUInverse : MD -> Record(Inv:MD, Pivots:L D) - ++ \axiom{LUInverse(A)} computes the inverse of \axiom{A} using a LU - ++ decomposition. - - - Def ==> add - - LUDecomp(AA:MD):Record(LU:MD, Perm:V I, Pivots:L D) == - -- LU decomposition using Crout's algorithm with partial pivoting. - A := copy AA - minR := minRowIndex A; maxR := maxRowIndex A - minC := minColIndex A; maxC := maxColIndex A - maxR~=maxC => error "LU decomposition only of square matrices" - PermV:V I := new((maxR-minR+1)::NNI,0) - Pivs:L D := empty - - for j in minC..maxC repeat - for i in minR..(j-1) repeat - s := qelt(A,i,j) - for k in minR..(i-1) repeat - s := s - qelt(A,i,k)*qelt(A,k,j) - qsetelt!(A,i,j,s) - - i0:I := -1 - for i in j..maxR repeat - s := qelt(A,i,j) - for k in minC..(j-1) repeat - s := s - qelt(A,i,k)*qelt(A,k,j) - qsetelt!(A,i,j,s) - if not(zero? s) and i0<0 then - i0 := i -- first non-zero pivot - - i0<0 => error "singular matrix in LUDecomp" - if j~=i0 then - swapRows!(A,j,i0) - qsetelt!(PermV,j,i0) - Pivs := cons(qelt(A,j,j),Pivs) - - if j~=maxC then - d := 1/qelt(A,j,j) - for k in (j+1)..maxR repeat - qsetelt!(A,k,j,d*qelt(A,k,j)) - - [A,PermV,Pivs] - - - LUSolve(LU:MD,Perm:V I,XX:V D):V D == - -- Solves LU decomposed linear system for right hand side XX - X := copy XX - minR := minRowIndex LU; maxR := maxRowIndex LU - maxIndex(X)~=maxR => error "Wrong dimensions in LUSolve" - ii:I := -1 - - for i in minR..maxR repeat -- forward substitution - ip := qelt(Perm,i) - s := qelt(X,ip) - qsetelt!(X,ip,qelt(X,i)) - if ii>=0 then - for j in ii..(i-1) repeat - s := s - qelt(LU,i,j)*qelt(X,j) - else - if not zero? s then ii := i - qsetelt!(X,i,s) - - for i in maxR..minR by -1 repeat -- back substitution - s := qelt(X,i) - for j in (i+1)..maxR repeat - s := s - qelt(LU,i,j)*qelt(X,j) - qsetelt!(X,i,s/qelt(LU,i,i)) - - X - - - LUInverse(A:MD):Record(Inv:MD, Pivots:L D) == - -- Inversion via LU decomposition - Alu := LUDecomp A - n := ncols A - res:MD := new(n,n,0) - - for i in minRowIndex(A)..maxRowIndex(A) repeat - v:V D := new(n,0) - qsetelt!(v,i,1) - res := setColumn!(res,i,LUSolve(Alu.LU,Alu.Perm,v)) - - [res,Alu.Pivots] -\end{spad} - - added: )expose LUDecomposition
LUDecomposition (LUD)
LU decomposition for ordinary matrices.
fricas
)expose LUDecomposition
LUDecomposition is now explicitly exposed in frame initial A:=matrix [[subscript('a,[10*i+j]) for i in 1..3] for j in 1..3]
![\label{eq1}\left[
\begin{array}{ccc}
{a_{11}}&{a_{21}}&{a_{31}}
\
{a_{12}}&{a_{22}}&{a_{32}}
\
{a_{13}}&{a_{23}}&{a_{33}}](images/69904982121776732-16.0px.png "\label{eq1}\left[
\begin{array}{ccc}
{a_{11}}&{a_{21}}&{a_{31}}
\
{a_{12}}&{a_{22}}&{a_{32}}
\
{a_{13}}&{a_{23}}&{a_{33}}") | (1) |
Type: Matrix(Polynomial(Integer))
fricas
diagProduct(x) == reduce(*,[x(i, i) for i in 1..nrows(x)])
Type: Void
fricas
B:=LUDecomp A;
Type: Record(LU: Matrix(Fraction(Polynomial(Integer))),
fricas
B.LU
![\label{eq2}\left[
\begin{array}{ccc}
{a_{11}}&{a_{21}}&{a_{31}}
\
{{a_{12}}\over{a_{11}}}&{{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}\over{a_{11}}}&{{{{a_{11}}\ {a_{32}}}-{{a_{12}}\ {a_{3
1}}}}\over{a_{11}}}
\
{{a_{13}}\over{a_{11}}}&{{{{a_{11}}\ {a_{23}}}-{{a_{13}}\ {a_{21}}}}\over{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}}&{{{{\left({{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}\right)}\ {a_{33}}}+{{\left(-{{a_{11}}\ {a_{23}}}+{{a_{13}}\ {a_{21}}}\right)}\ {a_{32}}}+{{\left({{a_{12}}\ {a_{23}}}-{{a_{13}}\ {a_{22}}}\right)}\ {a_{31}}}}\over{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}}](images/7437434583763855616-16.0px.png "\label{eq2}\left[
\begin{array}{ccc}
{a_{11}}&{a_{21}}&{a_{31}}
\
{{a_{12}}\over{a_{11}}}&{{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}\over{a_{11}}}&{{{{a_{11}}\ {a_{32}}}-{{a_{12}}\ {a_{3
1}}}}\over{a_{11}}}
\
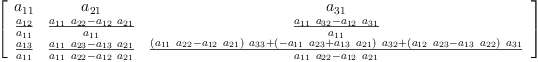{{a_{13}}\over{a_{11}}}&{{{{a_{11}}\ {a_{23}}}-{{a_{13}}\ {a_{21}}}}\over{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}}&{{{{\left({{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}\right)}\ {a_{33}}}+{{\left(-{{a_{11}}\ {a_{23}}}+{{a_{13}}\ {a_{21}}}\right)}\ {a_{32}}}+{{\left({{a_{12}}\ {a_{23}}}-{{a_{13}}\ {a_{22}}}\right)}\ {a_{31}}}}\over{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}}") | (2) |
Type: Matrix(Fraction(Polynomial(Integer)))
fricas
B.Perm
![\label{eq3}\left[ 1, \: 2, \: 3 \right]](images/5939555326889798646-16.0px.png "\label{eq3}\left[ 1, \: 2, \: 3 \right]") | (3) |
Type: Vector(Integer)
fricas
B.Pivots
![\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{{\left(
\begin{array}{@{}l}
\displaystyle
{{\left({{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}\right)}\ {a_{33}}}+
\
\
\displaystyle
{{\left(-{{a_{11}}\ {a_{23}}}+{{a_{13}}\ {a_{21}}}\right)}\ {a_{32}}}+
\
\
\displaystyle
{{\left({{a_{12}}\ {a_{23}}}-{{a_{13}}\ {a_{22}}}\right)}\ {a_{31}}}](images/3676745560049072994-16.0px.png "\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{{\left(
\begin{array}{@{}l}
\displaystyle
{{\left({{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}\right)}\ {a_{33}}}+
\
\
\displaystyle
{{\left(-{{a_{11}}\ {a_{23}}}+{{a_{13}}\ {a_{21}}}\right)}\ {a_{32}}}+
\
\
\displaystyle
{{\left({{a_{12}}\ {a_{23}}}-{{a_{13}}\ {a_{22}}}\right)}\ {a_{31}}}") | (4) |
Type: List(Fraction(Polynomial(Integer)))
fricas
diagProduct(B.LU)=determinant A
fricas
Compiling function diagProduct with type Matrix(Fraction(Polynomial(
Integer))) -> Fraction(Polynomial(Integer))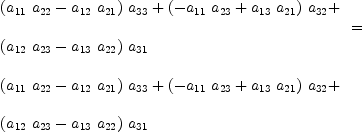![\label{eq5}\begin{array}{@{}l}
\displaystyle
{
\begin{array}{@{}l}
\displaystyle
{{\left({{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}\right)}\ {a_{33}}}+{{\left(-{{a_{11}}\ {a_{23}}}+{{a_{13}}\ {a_{21}}}\right)}\ {a_{32}}}+
\
\
\displaystyle
{{\left({{a_{12}}\ {a_{23}}}-{{a_{13}}\ {a_{22}}}\right)}\ {a_{31}}}](images/9056350525950241280-16.0px.png "\label{eq5}\begin{array}{@{}l}
\displaystyle
{
\begin{array}{@{}l}
\displaystyle
{{\left({{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}\right)}\ {a_{33}}}+{{\left(-{{a_{11}}\ {a_{23}}}+{{a_{13}}\ {a_{21}}}\right)}\ {a_{32}}}+
\
\
\displaystyle
{{\left({{a_{12}}\ {a_{23}}}-{{a_{13}}\ {a_{22}}}\right)}\ {a_{31}}}") | (5) |
Type: Equation(Fraction(Polynomial(Integer)))
fricas
%::Boolean
 | (6) |
Type: Boolean