One of the most frustrating things as a novice FriCAS user is to try to figure out how to get FriCAS output to appear in the desired form. For instance: fricas (1) -> (a + b)/2
Type: Polynomial(Fraction(Integer))
but if one wanted it formatted as a single fraction fricas (a + b)/2 :: FRAC POLY INT
Type: Fraction(Polynomial(Integer))
However, this doesn't always work: fricas 1/2 - exp(-t)
Type: Expression(Integer)
but if one wanted the output to appear as:
fricas 1/2 - exp(-t) :: POLY FRAC Integer this doesn't work. So how does one deal with output formatting for Expression Integers? In this particular case you have to say fricas 1/2 - exp(-t) :: EXPR FRAC INT
Type: Expression(Fraction(Integer))
since you have an expression here, not a polynomial. In general, to modify the way FriCAS outputs your expressions, you have to write a wrapper domain that replaces Here are some more detailed explanations: How can I affect the way FriCAS displays its results? Whenever FriCAS needs to write an element of a domain, i.e., an expression from
For example, to output a polynomial in factored form, the "real" way to do it is to coerce it into the domain Factored Polynomial Integer: fricas x^2-y^2
Type: Polynomial(Integer)
fricas (x^2-y^2)::Factored Polynomial Integer
Type: Factored(Polynomial(Integer))
Thus, philosophically, the way things are output depends only on the domain, and if we want to implement a different way, we need to implement a new domain. This is very easy, see DistributedExpression. How does this work in
|
| (8) |
z*a+z
| (9) |
since "z" is "larger" than "a". Of course, "larger" is simply a rather arbitrary, but fortunately fixed internal order of the variables. For Expressions, this order is not even fixed (but you can see difference only in some large, tricky cases).
Can I make FriCAS display 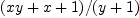 as
as 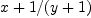 ?
?
As follows from the above, this currently cannot be done within the domain EXPR INT.
However, one can avoid combining subexpression with surrounding terms using
box operator:
x+box(1/(y+1))
| (10) |
Similarly, one can use paren operator to present expressions in factored form:
paren(exp(x) - x)*paren(exp(x) + x)
| (11) |
Note that box and paren inhibit normal simplification, so
paren(x) - x
| (12) |
will not simplify to 0. One needs to use distribute to cancel
effect of box or 'paren':
distribute(paren(x) - x)
| (13) |
I think that there are several possibilities, which I will explain on an old example, the problem of displaying expressions in "fully expanded" form:
- one can write a domain which only overrides the output functionality, and applies the simplifications every time the element is written on the screen. That's what I have done for DistributedExpression. This is the quick and dirty way.
- one writes a new domain with a new representation. For
DistributedExpressionI failed to do so, since the proper representation would beDMP, but this only accepts aList Symbolas variables, for expressions I need to allow an arbitraryOrderedSethowever. - one abstracts the form and writes a new functor, as for example
Factored. I'm not quite sure, but it may be that a functorDistributedwould be the best solution. I would have to look why the original developers chose to implementDistributedMultivariatePolynomialsinstead.
So, the conclusion is that you might want to write a function first that takes - for example - an expression and returns a list of expressions. It would be easy to make this into a new domain "MyExpression?". I vaguely recall that Maxima has such a function.