|
|
|
last edited 9 years ago by hemmeckie |
Edit detail for DancingSambaRamanujan revision 3 of 3
| 1 2 3 | ||
|
Editor: hemmeckie
Time: 2017/02/16 21:40:35 GMT+0 |
||
| Note: | ||
added:
http://dx.doi.org/10.1016/j.jsc.2017.02.001
http://www.risc.jku.at/publications/download/risc_5338/DancingSambaRamanujan.pdf
Dancing Samba with Ramanujan Partition Congruences
The following is complementary material to an article by Ralf Hemmecke.
http://dx.doi.org/10.1016/j.jsc.2017.02.001
http://www.risc.jku.at/publications/download/risc_5338/DancingSambaRamanujan.pdf
Ramanujan discovered that
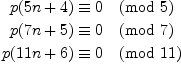
for all natural numbers ![]() where
where ![]() denotes the number of
partitions of
denotes the number of
partitions of ![]() .
.
The following witness identities were already known to Ramanujan.
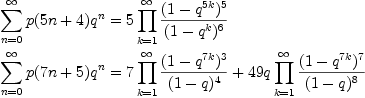
However, a similar identity for showing that p(11n+6) is divisible by 11 was not known.
Below we present such an identity. The algorithm "samba" (for subalgebra module basis algorithm) to obtain it, is described in the above article (which is accepted for publication in the Journal of Symbolic Computation).
Let us list the generators of the monoid of all quotients of
Dedekind ![]() -functions of level 22 that only have poles at infinity.
See the article by Silviu Radu for more detail:
-functions of level 22 that only have poles at infinity.
See the article by Silviu Radu for more detail:
@article{Radu:RamanujanKolberg:2015,
author = {Cristian-Silviu Radu},
title = {An algorithmic approach to {R}amanujan-{K}olberg
identities},
journal = {Journal of Symbolic Compuation,
volume = {68, Part 1},
pages = {225--253},
year = 2015,
issn = {0747-7171},
doi = {http://dx.doi.org/10.1016/j.jsc.2014.09.018},
url = {\url{http://www.sciencedirect.com/science/article/pii/S0747717114000868}},
keywords = {Partition identities, Number theoretic algorithm, Modular forms},
}
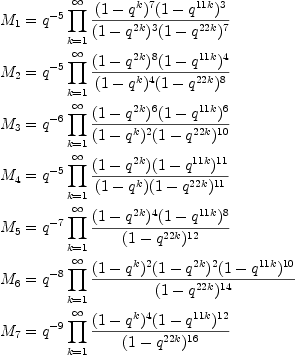
![]()
Then our witness identity for showing that p(11n+6) is divisible by 11 is this.
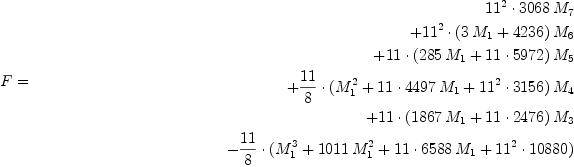
Note that this identity
does not involve ![]() .
.
Below, we show by means of the FriCAS computer algebra system that indeed the Laurent series agree up to a high order. Actually, by theory it is sufficient that the Laurent series agree in their coefficients for all negative powers and for the constant term.
(1) -> <spad> ------------------------------------------------------------------- --- --- FriCAS QFunctions --- Copyright (C) 2014-2015,Ralf Hemmecke <ralf@hemmecke.org> --- ------------------------------------------------------------------- -- This program is free software: you can redistribute it and/or modify -- it under the terms of the GNU General Public License as published by -- the Free Software Foundation, either version 3 of the License, or -- (at your option) any later version. -- -- This program is distributed in the hope that it will be useful, -- but WITHOUT ANY WARRANTY; without even the implied warranty of -- MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the -- GNU General Public License for more details. -- -- You should have received a copy of the GNU General Public License -- along with this program. If not, see <http://www.gnu.org/licenses/>. -------------------------------------------------------------------
)if LiterateDoc
\documentclass{article}
\usepackage{literatedoc}
\usepackage{amsmath,
\tableofcontents
\section{Overview}
In general we have:
\begin{align*}
(a; q)_n &=
\begin{cases}
1&\text{if $n=0$}\\
\prod_{k=0}^{n-1} (1-a q^k)& \text{if $n>0$}\\
\left(\prod_{k=1}^{-n} (1-\frac{a}{q^k})\right)^{-1}& \text{if $n<0$}\\
\end{cases}\\
(a; q)_{-n} &= \frac{1}{(aq^{-n}; q)_n}\qquad\text{if $n>0$}\\
(a; q) &= \prod_{k=0}^\infty (1-a q^k)
\end{align*}
\section{Implementation}
In the following we implement for $n\ge0$:
\begin{align*}
(c q^r; q^s)_n &= \prod_{k=0}^{n-1} (1-c q^{r+sk})\\
(c q^r; q^s)_{-n} &= \frac{1}{(cq^{r-sn}; q^s)_n}
\end{align*}
Note that if $s<0$ and $n>0$ then
\begin{align*}
(c q^r; q^s)_{n} &= \prod_{k=0}^{n-1} (1-c q^{r+sk})\\
&= \prod_{k=0}^{n-1} (1-c q^{r+s(n-1)-sk})\\
&= (c q^{r+s(n-1)}; q^{-s})
\end{align*}
Let $R$ be a ring and $i\in\setN$,
Define $g_i$ by $f_i = 1+q^{r+si} g_i$. Then we have
\begin{align*}
1+q^{r+si} g_i
&=(1+c_i q^{r+si})\cdot f_{i+1}\\
&=(1+c_i q^{r+si})\cdot (1+q^{r+s(i+1)} g_{i+1})\\
&=1+c_i q^{r+si}+ q^{r+s(i+1)} g_{i+1} + c_i q^{r+si+r+s(i+1)} g_{i+1}.
\end{align*}
Hence
\begin{align*}
g_i &=c_i + q^s g_{i+1} + c_i q^{r+s(i+1)} g_{i+1}\\
&=c_i + q^s(g_{i+1} + q^{r+si} c_i g_{i+1}).
\end{align*}
For the infinite case we have $c_i=c$ for all $i\in\setN$.
For the finite case,
For the infinite case,
)endif
)abbrev package QFUN QFunctions ++ Author: Ralf Hemmecke ++ Description: ++ Implement qPochhammer and friends. QFunctions(R: Ring,L: UnivariateLaurentSeriesCategory R): C == I where N ==> NonNegativeInteger P ==> PositiveInteger Z ==> Integer Rec ==> Record(k: Z, c: R) S ==> Stream Rec C ==> with qPochhammer: () -> L ++ qPochhammer() = qPochhammer(1, 1, 1) qPochhammer: R -> L ++ qPochhammer(c) = qPochhammer(c, 0, 1) eulerFunction: P -> L ++ For s>0, eulerFunction(s) = qPochhammer(1, s, s). ++ https://en.wikipedia.org/wiki/Euler_function ++ We use the Pentagonal number theorem to speed up ++ its computation. ++ https://en.wikipedia.org/wiki/Pentagonal_number_theorem ++ eulerFunction(s) = ++ 1 + \sum_{n>0} (-1)^n (q^(s*n*(3*n+1)/2) + q^(s*n*(3*n-1)/2)) partitionSeries: P -> L ++ partitionSeries(s) returns the partition generating series, i.e., ++ the coefficient of $q^(s*n)$ is the number of partitions of $n$ ++ (where $q$ is the variable from $L$). ++ It holds: partitionSeries(s)*eulerFunction(s)=1. qPochhammer: (R, N) -> L ++ qPochhammer(c, n) = qPochhammer(c, 0, 1, n) qPochhammer: (R, Z, P) -> L ++ qPochhammer(c, r, s) returns the Laurent series given by ++ \[(c\cdot q^r, q^s)= ++ \[\prod_{k=0}^{\infty} (1-c\cdot q^s \cdot (q^r)^k)\] ++ where q=monomial(1, 1)$L. qPochhammer: (R, Z, Z, N) -> L ++ qPochhammer(c, r, s, n) returns the Laurent series ++ $(c\cdot q^r, q^s)_n$ given by 1, if n=0; ++ and ++ \[\prod_{k=0}^{n-1} (1-c\cdot q^s \cdot (q^r)^k), \] otherwise, ++ where q=monomial(1, 1)$L.
I ==> add qPochhammer(): L == qPochhammer(1,1, 1) qPochhammer(c: R): L == qPochhammer(c, 0, 1) qPochhammer(c: R, n: N): L == qPochhammer(c, 0, 1, n)
-- prepend(n,c, st) returns a stream whose first n elements are -- c followed by the original stream st. -- Input condition: n>=0. prepend(n: Z, c: R, st: Stream R): Stream R == delay zero? n => st concat(c, prepend(n-1, c, st))
-- computes x + c * y plus(x: Stream R,c: R, y: Stream R): Stream R == delay empty? x => map((k: R): R +-> c*k, y) empty? y => x concat(frst x + c*frst(y), plus(rst x, c, rst y))
-- This computes x+c*q^n*y. -- Input condition: n>=0. qpauxrec(x: Stream R,c: R, n: Z, y: Stream R): Stream R == delay zero? n => plus(x, c, y) empty? x => prepend(n, 0$R, map((k: R): R +-> c*k, y)) concat(frst x, qpauxrec(rst x, c, n-1, y))
-- This computes (1+c*q^n)*g. -- Input condition: n>=0. qpaux(c: R,n: Z, g: Stream R): Stream R == qpauxrec(g, c, n, g)
-- Computes g_i from description above or rather g(r,s), but we -- needed a count n, so that we know when to abort the recursion. -- Input condition: r>=0, s>0, n>=0. qPochhammerAuxN(c: R, r: Z, s: Z, n: Z): Stream R == delay zero? n => empty()$Stream(R) g: Stream R := qPochhammerAuxN(c, r+s, s, n-1) empty? g => concat(c, g) concat(c, prepend(s-1, 0, qpaux(c, r, g)))
-- This computes (c*q^r; q^s)_n. -- Input condition: r>=0,s>0, n>=0. qPochhammerPos(c: R, r: Z, s: Z, n: Z): L == zero? c => 1$L 1 + laurent(r, qPochhammerAuxN(-c, r, s, n))
-- This computes (c*q^r; q^s)_n. -- Input condition. n>=0. -- It is intended for the case r<0,r+s<0, ..., r+s*(n-1)<0. qPochhammerNeg(c: R, r: Z, s: Z, n: Z): L == zero? n => 1$L c: R := -c l: L := 1 + monomial(c, r) for i in 1..n-1 repeat l := l + monomial(c, r+s*i)*l l
-- This computes (c*q^r; q^s)_n for n>=0. qPochhammer(c: R,r: Z, s: Z, n: N): L == zero? n => 1$L -- assert(n>0) zero? r => cc: R := 1-c zero? cc => 0$L cc * qPochhammer(c, s, s, qcoerce(n-1)@N) zero? s => (1 + monomial(-c, r))^n -- s=0 is supposed to be a rare case s < 0 => r > 0 => qPochhammer(c, r+s*(n-1), -s, n) qPochhammerNeg(c, r, s, n) -- assert(s>0) r > 0 => qPochhammerPos(c, r, s, n) -- assert(r<0) j: Z := (-r) quo s -- j >= 0 -- find splitting point pos/neg -- assert(r+s*j<=0) cc: R := -c j >= n => qPochhammerNeg(c, r, s, n) zero?(r+s*j) => -- we have an R-factor in the middle cc: R := 1-c zero? cc => 0$L ln: L := qPochhammerNeg(c, r, s, j) lp: L := qPochhammerPos(c, r+s*(j+1), s, qcoerce(n-1-j)@N) cc * ln * lp ln: L := qPochhammerNeg(c, r, s, j+1) lp: L := qPochhammerPos(c, r+s*(j+1), s, qcoerce(n-1-j)@N) ln * lp
-- Computes g_i from description above or rather g(r,s). -- Input condition: r>0, s>0. qPochhammerAux(c: R, r: Z, s: Z): Stream R == delay concat(c, prepend(s-1, 0, qpaux(c, r, qPochhammerAux(c, r+s, s))))
-- This computes (a*q^r; q^s)_\infty. qPochhammer(a: R,r: Z, s: P): L == zero? a => 1$L zero? r => aa: R := 1-a zero? aa => 0$L aa * qPochhammer(a, s, s) RX ==> SparseUnivariatePolynomial R a := -a p: RX := 1 while r < 0 repeat p := p + monomial(a, qcoerce(-r)@N)$RX * p r := r + s l: L := 1 + laurent(r, qPochhammerAux(a, r, s)) one? p => l terms: S := [[-degree m, leadingCoefficient m]$Rec for m in monomials p]::S l*series(terms)$L
-- This computes (q^s; q^s)_\infty. -- Input condition: s>0. -- eulerFunction(s: P): L == 1 + laurent(s,qPochhammerAux(-1, s, s)) -- Faster version of eulerFunctions building on the Pentagonal number -- theorem. eulerStream(s: P, n: Z, m: Z, z: S): S == delay r: R := if even? n then 1 else -1 cons([s*m, r], cons([s*(2*n+1+m), -r], eulerStream(s, n+1, m+3*n+2, z))) eulerFunction(s: P): L == series eulerStream(s, 0, 0, empty()$S) partitionSeries(s: P): L == recip(eulerFunction s)::L
)if LiterateDoc
\end{document}
)endif
N ==> NonNegativeInteger
)abbrev package QFUNTOOL QFunctionTools ++ QFunctionTools allows to create a series from another series. QFunctionTools(C: Ring,L: UnivariateLaurentSeriesCategory C): with choose: (N -> N, L) -> L ++ choose(f, x) returns the power series whose n-th coefficient ++ is the f(n)-th coefficient of x. == add streamAux(n: N, f: N -> N, x: L): Stream C == delay cons(coefficient(x, f n), streamAux(n+1, f, x)) chooseStream(f: N -> N, x: L): Stream C == streamAux(0, f, x) choose(f: N -> N, x: L): L == laurent(0, chooseStream(f, x))</spad>
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/1402996769419034555-25px001.spad
using old system compiler.
QFUN abbreviates package QFunctions
------------------------------------------------------------------------
initializing NRLIB QFUN for QFunctions
compiling into NRLIB QFUN
compiling exported qPochhammer : () -> L
Time: 0.03 SEC.
compiling exported qPochhammer : R -> L
Time: 0 SEC.
compiling exported qPochhammer : (R,
compiling local prepend : (Integer,
compiling local plus : (Stream R,
compiling local qpauxrec : (Stream R,
compiling local qpaux : (R,
compiling local qPochhammerAuxN : (R,
compiling local qPochhammerPos : (R,
compiling local qPochhammerNeg : (R,
compiling exported qPochhammer : (R,
compiling local qPochhammerAux : (R,
compiling exported qPochhammer : (R,
compiling local eulerStream : (PositiveInteger,
compiling exported eulerFunction : PositiveInteger -> L
Time: 0 SEC.
compiling exported partitionSeries : PositiveInteger -> L
Time: 0 SEC.
(time taken in buildFunctor: 0)
Time: 0 SEC.
Cumulative Statistics for Constructor QFunctions
Time: 0.15 seconds
finalizing NRLIB QFUN
Processing QFunctions for Browser database:
--------constructor---------
--------(qPochhammer (L))---------
--------(qPochhammer (L R))---------
--------(eulerFunction (L (PositiveInteger)))---------
--->-->QFunctions((eulerFunction (L (PositiveInteger)))): Improper first word in comments: For
--->-->QFunctions((eulerFunction (L (PositiveInteger)))): Unexpected HT command: \sum_
"For \\spad{s>0},
; wrote /var/aw/var/LatexWiki/QFUN.NRLIB/QFUN.fasl
; compilation finished in 0:00:00.064
------------------------------------------------------------------------
QFunctions is now explicitly exposed in frame initial
QFunctions will be automatically loaded when needed from
/var/aw/var/LatexWiki/QFUN.NRLIB/QFUN
QFUNTOOL abbreviates package QFunctionTools
------------------------------------------------------------------------
initializing NRLIB QFUNTOOL for QFunctionTools
compiling into NRLIB QFUNTOOL
compiling local streamAux : (NonNegativeInteger,
compiling local chooseStream : (NonNegativeInteger -> NonNegativeInteger,
compiling exported choose : (NonNegativeInteger -> NonNegativeInteger,
(time taken in buildFunctor: 0)
Time: 0 SEC.
Cumulative Statistics for Constructor QFunctionTools
Time: 0.02 seconds
finalizing NRLIB QFUNTOOL
Processing QFunctionTools for Browser database:
--------constructor---------
--------(choose (L (Mapping (NonNegativeInteger) (NonNegativeInteger)) L))---------
; compiling file "/var/aw/var/LatexWiki/QFUNTOOL.NRLIB/QFUNTOOL.lsp" (written 22 NOV 2025 12:34:11 AM):
; wrote /var/aw/var/LatexWiki/QFUNTOOL.NRLIB/QFUNTOOL.fasl
; compilation finished in 0:00:00.004
------------------------------------------------------------------------
QFunctionTools is now explicitly exposed in frame initial
QFunctionTools will be automatically loaded when needed from
/var/aw/var/LatexWiki/QFUNTOOL.NRLIB/QFUNTOOLN ==> NonNegativeInteger
P ==> PositiveInteger
Z ==> Integer
Q ==> Fraction Z
C ==> Q
L ==> UnivariateLaurentSeries(Q,'q, 0)
ef ==> eulerFunction$QFunctions(Q,L)
q: L := 'q:: L
| (1) |
qPower(n: P,e: Z): L == (_ zero? e => 1;_ e > 0 => expt(ef n, qcoerce(e)@P)$RepeatedSquaring(L);_ inv(expt(ef n, qcoerce(-e)@P)$RepeatedSquaring(L)));
Function declaration qPower : (PositiveInteger,Integer) -> UnivariateLaurentSeries(Fraction(Integer), q, 0) has been added to workspace.
qQuotient(s: Z,r: List Z): L == (_ divs: List P := [1, 2, 11, 22];_ q^s * reduce(_*, [qPower(d, e) for d in divs for e in r], 1)$List(L));
Function declaration qQuotient : (Integer,List(Integer)) -> UnivariateLaurentSeries(Fraction(Integer), q, 0) has been added to workspace.
qQuotients(): List L == (_ [qQuotient(s,r) _ for s in [-5, -5, -6, -5, -7, -8, -9] _ for r in [[7, -3, 3, -7], [-4, 8, 4, -8], [-2, 6, 6, -10], _ [-1, 1, 11, -11], [0, 4, 8, -12], [2, 2, 10, -14], [4, 0, 12, -16]]]);
Function declaration qQuotients : () -> List(UnivariateLaurentSeries (Fraction(Integer),q, 0)) has been added to workspace.
M := qQuotients();
Compiling function qPower with type (PositiveInteger,Integer) -> UnivariateLaurentSeries(Fraction(Integer), q, 0)
Compiling function qQuotient with type (Integer,List(Integer)) -> UnivariateLaurentSeries(Fraction(Integer), q, 0)
Compiling function qQuotients with type () -> List(
UnivariateLaurentSeries(Fraction(Integer),p: L := partitionSeries(1)$QFunctions(Q,L)
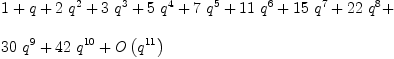 | (2) |
r11: L := choose((n: N): N +-> 11*n+6,p)
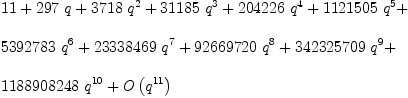 | (3) |
prefactor: L := qQuotient(-14,[10, 2, 11, -22])
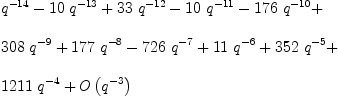 | (4) |
F := prefactor * r11
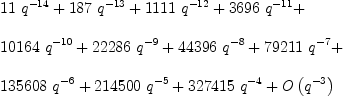 | (5) |
R := 11^2*3068*M.7+ 11^2*(3*M.1+4236)*M.6 +11*(285*M.1+11*5972)*M.5+11/8*((M.1)^2+11*4497*M.1+11^2*3156)*M.4+11*(1867*M.1+11*2476)*M.3-11/8*((M.1)^3+1011*(M.1)^2+11*6588*M.1+11^2*10880);
d := R - F
| (6) |
Obviously, the Laurent series ![]() does not have nonzero coefficients for negative powers of
does not have nonzero coefficients for negative powers of ![]() .
In fact, it is identically 0, but due to the fact that it is a Laurent series, it cannot be proven
algorithmically, although by the respective theory developed by Silviu Radu,
.
In fact, it is identically 0, but due to the fact that it is a Laurent series, it cannot be proven
algorithmically, although by the respective theory developed by Silviu Radu,
![]() must be identically 0, if its order is greater than 0.
must be identically 0, if its order is greater than 0.
Below we show that indeed the coefficients of the difference series from q^0 to q^100 vanish. In FriCAS, Laurent series are (not like in other computer algebra systems) truncated series, but rather the information about ALL coefficients is stored lazily and can now be extracted.
[coefficient(d,k) for k in 0..100]
![\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[ 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \right.
\
\
\displaystyle
\left.\: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \right.
\
\
\displaystyle
\left.\: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \right.
\
\
\displaystyle
\left.\: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0 \right]
\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[ 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \right.
\
\
\displaystyle
\left.\: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \right.
\
\
\displaystyle
\left.\: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \right.
\
\
\displaystyle
\left.\: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0 \right]](images/7867698721529303243-16.0px.png) | (7) |