help links subscribe changes refresh edit

	IssueTracker
#29 for i in 1..1 repeat print(sin(i) :: Complex Float) ←	↑	→ #291 small typo in docs

#290 Axiom failed to integrate elementary function

Edit detail for #290 Axiom failed to integrate elementary function revision 1 of 3

	1 2 3
Editor: Time: 2007/11/17 22:22:01 GMT-8
Note: Related example

changed:
-
When I type:
\begin{axiom}
ex1:=(x-x/(x+exp(x)/(x*log(x+x))))*exp(2)
ex2:=D(ex1, x)
ex3:=simplify(ex2)
integrate(ex3, x)
\end{axiom}
then Axiom 3.9 returns unevaluated integral. 

Note, that if I remove the exp(2) factor, then Axiom is able to
compute the integral.
\begin{axiom}
ex4:=(x-x/(x+exp(x)/(x*log(x+x))))
ex5:=D(ex4, x)
ex6:=simplify(ex5)
integrate(ex6, x)
\end{axiom}

From kratt6 Wed May 10 01:28:56 -0500 2006
From: kratt6
Date: Wed, 10 May 2006 01:28:56 -0500
Subject: We claim that Axiom is good at integration, therefore critical
Message-ID: <20060510012856-0500@wiki.axiom-developer.org>

Severity: normal => critical 


From kratt6 Wed May 10 01:29:14 -0500 2006
From: kratt6
Date: Wed, 10 May 2006 01:29:14 -0500
Subject: We claim that Axiom is good at integration, therefore critical
Message-ID: <20060510012914-0500@wiki.axiom-developer.org>

Category: Axiom Mathematics => Axiom Library 


From unknown Wed May 10 06:22:25 -0500 2006
From: unknown
Date: Wed, 10 May 2006 06:22:25 -0500
Subject: Related example
Message-ID: <20060510062225-0500@wiki.axiom-developer.org>

If I try:
\begin{axiom}
integrate(simplify(((x^4*log(2*x)^2+(3*x^2-2*x)*exp(x)*log(2*x)+exp(2*x)-x*exp(x))/(x^4*log(2*x)^2+2*x^2*exp(x)*log(2*x)+exp(2*x))-1)*exp(2)), x)
\end{axiom}
I see that Axiom failed to recognize that e^4 - (e^2)^2 is
zero. AFAICS similar problem appears in original example:
when I trace rischNormalize I see that both e^2 and e^4
appear in "normalized" function. But this may cause
trouble later, since Axiom assumes that different kernels
are algebraically independent. 
I do not know if rischNormalize is supposed to simplify
constants (maybe this shoud be done by a separtate pass)
but failing to recognize "transcendental" zero may give
wrong results and otherwise Risch algorithm may declare
an integrable function as non integrable.

When I type:

axiom

ex1:=(x-x/(x+exp(x)/(x*log(x+x))))*exp(2)

(1)

Type: Expression Integer

axiom

ex2:=D(ex1, x)

(2)

Type: Expression Integer

axiom

ex3:=simplify(ex2)

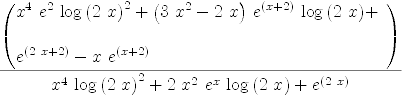(3)

Type: Expression Integer

axiom

integrate(ex3, x)

(4)

Type: Union(Expression Integer,...)

then Axiom 3.9 returns unevaluated integral.

Note, that if I remove the exp(2) factor, then Axiom is able to compute the integral.

axiom

ex4:=(x-x/(x+exp(x)/(x*log(x+x))))

(5)

Type: Expression Integer

axiom

ex5:=D(ex4, x)

(6)

Type: Expression Integer

axiom

ex6:=simplify(ex5)

(7)

Type: Expression Integer

axiom

integrate(ex6, x)

(8)

Type: Union(Expression Integer,...)

We claim that Axiom is good at integration, therefore critical --kratt6, Wed, 10 May 2006 01:28:56 -0500 reply

Severity: normal => critical

We claim that Axiom is good at integration, therefore critical --kratt6, Wed, 10 May 2006 01:29:14 -0500 reply

Category: Axiom Mathematics => Axiom Library

Related example --unknown, Wed, 10 May 2006 06:22:25 -0500 reply

If I try:

axiom

integrate(simplify(((x^4*log(2*x)^2+(3*x^2-2*x)*exp(x)*log(2*x)+exp
(2*x)-x*exp(x))/(x^4*log(2*x)^2+2*x^2*exp(x)*log(2*x)+exp(2*
;x))-1)*exp(2)), x)

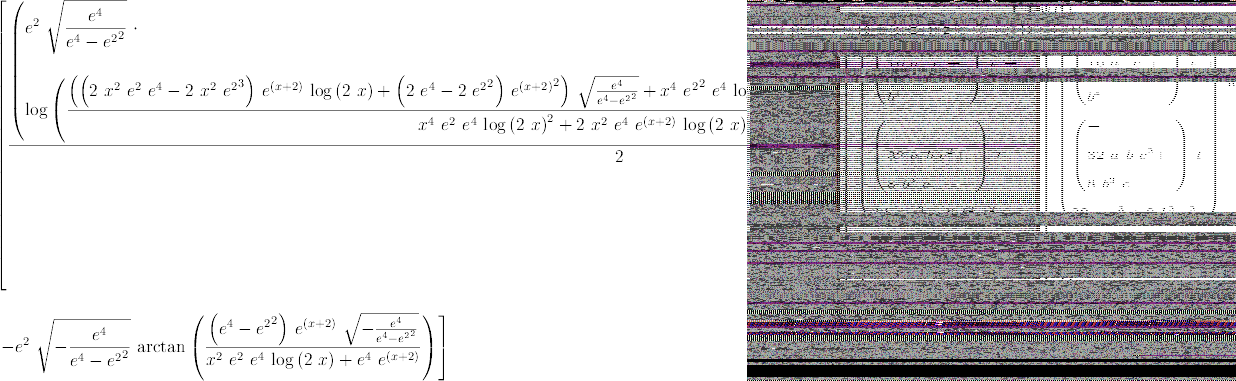(9)

Type: Union(List Expression Integer,...)

I see that Axiom failed to recognize that e^4 - (e^2)^2 is zero. AFAICS similar problem appears in original example: when I trace rischNormalize I see that both e^2 and e^4 appear in "normalized" function. But this may cause trouble later, since Axiom assumes that different kernels are algebraically independent. I do not know if rischNormalize is supposed to simplify constants (maybe this shoud be done by a separtate pass) but failing to recognize "transcendental" zero may give wrong results and otherwise Risch algorithm may declare an integrable function as non integrable.