|
|
|
last edited 16 years ago by kratt6 |
Edit detail for #263 ContinuedFraction returns incorrect types revision 2 of 3
| 1 2 3 | ||
|
Editor: kratt6
Time: 2007/12/05 05:44:59 GMT-8 |
||
| Note: typo and refresh | ||
changed: -'Fraction Fraction Integer' is also nonesense. 'Fraction Fraction Integer' is also nonsense.
There seems to be a problem with Axiom's ContinuedFractions? domain.
The type of the result is shown as Fraction Float but this is
nonesense.
Something similar happens if the argument is Fraction Integer
axiom)set functions compile on nume(a) == cons(1,[((a-i)*i) for i in 1..]);
axiomdene(a,x) == [(x+2*i+1-a) for i in 0..];
axiomcfe(a,x) == continuedFraction(0,nume(a),dene(a,x));
axiomccfe(a,x) == convergents cfe(a,x);
axiomccfe(0,2::Float)
Compiling function nume with type NonNegativeInteger -> Stream
IntegerCompiling function dene with type (NonNegativeInteger,Float) ->
Stream FloatCompiling function cfe with type (NonNegativeInteger,Float) ->
ContinuedFraction FloatCompiling function ccfe with type (NonNegativeInteger,Float) ->
Stream Fraction Float | (1) |
axiomccfe(0,2::Fraction Integer)
Compiling function dene with type (NonNegativeInteger,Fraction
Integer) -> Stream Fraction IntegerCompiling function cfe with type (NonNegativeInteger,Fraction
Integer) -> ContinuedFraction Fraction IntegerCompiling function ccfe with type (NonNegativeInteger,Fraction
Integer) -> Stream Fraction Fraction Integer| (2) |
Fraction Fraction Integer is also nonsense.
axiomff1:Fraction Float Fraction Float is not a valid type. ff2:Fraction Fraction Integer Fraction Fraction Integer is not a valid type.
R, it is often natural to return something of type Fraction R. I see two possible solutions:
Fraction RreturnsRwhenRis a field- an operation that wants to return
Fraction Rhas to check whetherRis a field.
In the case above I see another problem:
axiomn := nume(0.2)
Compiling function nume with type Float -> Stream Float
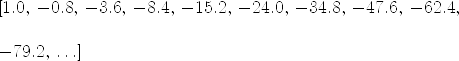 | (3) |
axiomd := dene(0.2,x)
Compiling function dene with type (Float,Variable x) -> Stream
Polynomial Float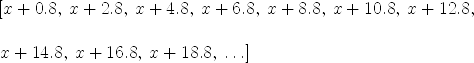 | (4) |
axiomcontinuedFraction(0, n, d)
(note that there is no output...)
This makes very good sense to me. Is Field the right type or something more general?But is this possible in Axiom? How would I modify [Fraction]? to make this happen?
Thinking about it, I realized that this is not the proper solution, sinceFraction R provides some operations, for example denominator which R does not necessarily have and I think it would be wrong to equip every Field with this operation, which would then be necessary. Thus, either
- Axiom's interpreter should not complain about types like
Fraction Float. In this case,denominatorwill always return1, of course. Note that you can perfectly well calculate with objects of typeStream Fraction Fraction Integer, no problem occurs. Or - operations that want to return Fraction R have to check whether R is a field.
The code that excludes constructions like FRAC FRAC and FRAC R when R is a field is in clammed.boot.pamphlet, lines 108-112.
Possibly we want to allow Fraction Field but disallow Fraction Fraction?
Martin
Since "add { ... }" is a value in Aldor/Axiom, [Fraction]? should/could be implemented as follows:spadFraction(S: IntegralDomain): QuotientFieldCategory S with ... == if S has Field then S add -- additional functions like "denom" etc. else ... add -- old code goes here
Compiling FriCAS source code from file
/var/zope2/var/LatexWiki/3103239194962224468-25px004.spad using
old system compiler.
******** Boot Syntax Error detected ********
The current line is:
0> ...
^
Currently preparsed lines are:
1> == if S has Field
2> then S add
4> else ...
5> add
The number of valid tokens is 1.
The current token is
Structure of type TOKEN
Byte:[Slot Type]Slot Name :Slot Value
0:SYMBOL :|..|
8:TYPE :GLIPH
16:NONBLANK :T
The prior token was
Structure of type TOKEN
Byte:[Slot Type]Slot Name :Slot Value
0:SYMBOL :|with|
8:TYPE :IDENTIFIER
16:NONBLANK :TWell, that means the representation of FRAC S depends on whether S is already a field or not.
I think Axiom's two-level type system is going to get in the way. Although it is true that types in Axiom are "first order objects" in the sense that we can assign them to variables etc., the kind of things that we can actually do with them is very limited. For example, I see no way in Axiom, SPAD or Aldor to have:
FRAC FRAC INT = FRAC INT
since FRAC INT is static type and FRAC FRAC INT is another
static type. In Axiom there is no way to write a function which
returns different types depending on it's parameters:
fType(x) ==
x=0 ==> Integer
Float
t:fType(1):=1.0
because types like Integer and Float are not members of some
domain in the same since in which 1 and -1 are members of
Integer. And further there is no equality defined over types.
Or do I not understand something quite fundamental here?
Perhaps what you are suggesting amounts to ensuring that, as types these two are at least functionally equivalent?
Martin wrote:Note that you can perfectly well calculate with objects of type Stream Fraction Fraction Integer, no problem occurs.
I don't think you can calculate reliably with these strange types. I get bizarre results and sometimes Axiom crashes when I try things that should work. For example, this works:
axiomcff1:=continuedFraction(0,repeating [2],repeating [3])
| (5) |
axiom4*cff1
| (6) |
axiomcff2:=continuedFraction(0,repeating [1/2],repeating [1/3])
| (7) |
But the following code sends Axiom into an infinite loop:
1/4*cff2