help links subscribe changes refresh edit

	IssueTracker
#190 Compile fail on Fedora Core 4 ←	↑	→ #192 Folding does not work in Konqueror 3.1.4

#191 exquo and therefore gcd cannot handle UP(x, EXPR INT)

Edit detail for #191 exquo and therefore gcd cannot handle UP(x, EXPR INT) revision 3 of 6

	1 2 3 4 5 6
Editor: test1 Time: 2015/04/21 17:37:27 GMT+0
Note:

removed:
-	gcd((x-2^a)::UP(x, EXPR INT), simplify((x-2^a)*(x+2^a))::UP(x, EXPR INT))
-
-gives 1, while the correct answer should be x-2^a, as given by
-
-gcd((x-2^a)::UP(x, EXPR INT),((x-2^a)*(x+2^a))::UP(x, EXPR INT))
-
-A workaround is presented on [EXPR_GCD]
-

changed:
-  In EXPR INT, $2^a$ and $2^{(2a)}$ are treated as two variables
-without relations in EXPR INT. Therefore exquo in::
-
-  gcdPrimitive(p1:SUPP,p2:SUPP)$PGCD
-
-fails.
-
-Thu 09/30/2004 at 09:31, comment !#3
-
-Excuse me, I was to quick again. Here is the (hopefully correct)
-anaylysis::
-
-  exquo(simplify((A-2^a)*(A+2^a))::UP(A,EXPR INT),(A-2^a)::UP(A,EXPR INT))
-
-calls 'exquo$SUP(EXPR INT)'. This implements exact division of
In EXPR INT,  $4^a$ and $2^{(2a)}$ are treated as two variables
without relations in EXPR INT.  But
\begin{axiom}
simplify((x-2^a)*(x+2^a))::UP(x, EXPR INT)
\end{axiom}


Therefore exquo in::

  exquo(simplify((x-2^a)*(x+2^a))::UP(x,EXPR INT),(x-2^a)::UP(x,EXPR INT))

fails.  In details, it calls 'exquo$UP(x,EXPR INT)'. This implements exact division of

changed:
-'fmecg$SUP' - the result is again stored in p1. exquo terminates
-when p1 is the empty list - note that SUPs are stored as lists
'fmecg$UP' - the result is again stored in p1. exquo terminates
when p1 is the empty list - note that UPs are stored as lists

changed:
-mathematically, but axiom does not know it. In particular,
mathematically, but FriCAS does not know it. In particular,

changed:
-It would be interesting to see how MuPAD or Aldor handle this.
-
-Martin Rubey <kratt6>
-
-Wed 09/29/2004 at 16:20, comment !#2:
-
-  The instance of exquo involved is the one in SMP.
-
-Sorry, this is not correct. It is in FIELD (for EXPR INT)
-
-Martin Rubey <kratt6>
To get correct result we need to express coefficients of p1 and p2
in terms of independent kernels.


changed:
-one in SMP.
one in SUP.

(new) exquo and therefore gcd cannot handle UP(x, EXPR INT) --Bill Page, Mon, 11 Jul 2005 15:56:25 -0500 reply

Update of bug #10530 (project axiom):

Status: None => transferred

fricas

gcd((x-2^a)::UP(x, EXPR INT), simplify((x-2^a)*(x+2^a))::UP(x, EXPR INT))

$\label{eq1}1$

(1)

Type: UnivariatePolynomial?(x,Expression(Integer))

Gives 1, while the correct answer should be 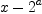, as given by

fricas

gcd((x-2^a)::UP(x, EXPR INT),((x-2^a)*(x+2^a))::UP(x, EXPR INT))

$\label{eq2}x -{{2}^{a}}$

(2)

Type: UnivariatePolynomial?(x,Expression(Integer))

Internal Cause

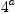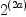In EXPR INT, and $2^{(2a)}$ are treated as two variables without relations in EXPR INT. But

fricas

simplify((x-2^a)*(x+2^a))::UP(x, EXPR INT)

$\label{eq3}{{x}^{2}}-{{4}^{a}}$

(3)

Type: UnivariatePolynomial?(x,Expression(Integer))

Therefore exquo in:

  exquo(simplify((x-2^a)*(x+2^a))::UP(x,EXPR INT),(x-2^a)::UP(x,EXPR INT))

fails. In details, it calls exquo$UP(x,EXPR INT). This implements exact division of polynomials p1 by p2 as usual. After each subtraction - done via fmecg$UP - the result is again stored in p1. exquo terminates when p1 is the empty list - note that UPs? are stored as lists of pairs (degree, coefficient) - or the degree of p2 is larger than p1. In the latter case, exquo fails.

Thus, in our case, at one point p1 is 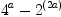$4^a-2^{(2a)}$ , which is zero mathematically, but FriCAS? does not know it. In particular, p1 is not the empty list, but rather a constant polynomial...

To get correct result we need to express coefficients of p1 and p2 in terms of independent kernels.

Wed 09/29/2004 at 16:02, comment #1:

I should have added:

fricas

exquo(normalize(simplify(((A-2^a)*(A+2^a)))::EXPR INT),normalize((A-2^a)::EXPR INT))

$\label{eq4}{{{e}^{a \ {\log \left({4}\right)}}}-{{A}^{2}}}\over{{{e}^{a \ {\log \left({2}\right)}}}- A}$

(4)

Type: Union(Expression(Integer),...)

fricas

exquo(simplify((A-2^a)*(A+2^a))::UP(A,EXPR INT),(A-2^a)::UP(A,EXPR INT))

$\label{eq5}\verb#"failed"#$

(5)

Type: Union("failed",...)

I'm afraid that this cannot be fixed easily, since there is no general mechanism to determine whether an expression is zero or not, which is needed in exquo. The instance of exquo involved is the one in SUP.

$2^{{a2}}$ vs --billpage, Wed, 13 Jul 2005 00:47:27 -0500 reply

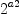
The problem seems to be that Axiom does not always treat $2^{a2}$ the same as

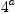
fricas

dom:=UP('x,EXPR INT)

$\label{eq6}\hbox{\axiomType{UnivariatePolynomial}\ } (x , \hbox{\axiomType{Expression}\ } (\hbox{\axiomType{Integer}\ }))$

(6)

Type: Type

fricas

p:dom:=x-2^a

$\label{eq7}x -{{2}^{a}}$

(7)

Type: UnivariatePolynomial?(x,Expression(Integer))

fricas

q:=(x-2^a)*(x+2^a)

$\label{eq8}-{{{2}^{a}}^{2}}+{{x}^{2}}$

(8)

Type: Expression(Integer)

fricas

qq:= simplify(q)

$\label{eq9}-{{4}^{a}}+{{x}^{2}}$

(9)

Type: Expression(Integer)

fricas

r:= q::dom

$\label{eq10}{{x}^{2}}-{{{2}^{a}}^{2}}$

(10)

Type: UnivariatePolynomial?(x,Expression(Integer))

fricas

rr:= qq::dom

$\label{eq11}{{x}^{2}}-{{4}^{a}}$

(11)

Type: UnivariatePolynomial?(x,Expression(Integer))

fricas

gcd(p,q)

$\label{eq12}x -{{2}^{a}}$

(12)

Type: UnivariatePolynomial?(x,Expression(Integer))

fricas

exquo(q,p)

$\label{eq13}{{2}^{a}}+ x$

(13)

Type: Union(Expression(Integer),...)

fricas

gcd(p,r)

$\label{eq14}x -{{2}^{a}}$

(14)

Type: UnivariatePolynomial?(x,Expression(Integer))

fricas

gcd(p,qq)

$\label{eq15}1$

(15)

Type: UnivariatePolynomial?(x,Expression(Integer))

fricas

gcd(p,rr)

$\label{eq16}1$

(16)

Type: UnivariatePolynomial?(x,Expression(Integer))

fricas

q - qq

$\label{eq17}{{4}^{a}}-{{{2}^{a}}^{2}}$

(17)

Type: Expression(Integer)

fricas

simplify q - qq

$\label{eq18}0$

(18)

Type: Expression(Integer)

fricas

simplify ((r - rr)::EXPR INT)

$\label{eq19}0$

(19)

Type: Expression(Integer)

fricas

t:Boolean:=(r = rr)

$\label{eq20} \mbox{\rm false}$

(20)

Type: Boolean

Comments from wyscc:

Martin wrote:

I'm afraid that this cannot be fixed easily, since there is no general mechanism to determine whether an expression is zero or not, which is needed in exquo.

Your analysis seems to be the correct diagnosis. The problem has nothing to do with gcd or exquo, but with the fact that simplification is an art as there is no canonical form for expressions and hence no way to test equality (which is in general different from testing zero, a special case needed for exquo). More frequent use of simplification will help but will not eliminate the problem. 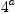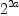Here, it is because the expressions and $2^{2a}$ are not handled by an automatic simplification in UP(x, R) (that is, not pushed down to the level of R).

property change --billpage, Tue, 12 Jul 2005 22:06:08 -0500 reply

Category: => Axiom Compiler Severity: => serious Status: => open

... --kratt6, Thu, 20 Dec 2007 01:07:34 -0800 reply

Category: Axiom Compiler => Axiom Library