login  home  contents  what's new  discussion  bug reports     help  links  subscribe  changes  refresh  edit
IssueTracker
#119 solve returns wrong answers and multiple answers to same trig problem  ← ↑ →  #120 optimize the compilation with proclamation

#12 radicalSolve fails to find all roots ?
  
last edited 17 years ago by kratt6

Edit detail for #12 radicalSolve fails to find all roots ? revision 1 of 2
1 2
Editor:
Time: 2007/11/17 21:55:37 GMT-8
Note: 
changed:
-
From -- William Sit

Subject -- Re: [Axiom-developer] [Q] radicalSolve fails to find all roots ?

Date -- Mon, 17 Jan 2005 16:31:52 -0500

These are NOT bugs! But the following may be! Consider the equation $z^n=1$ for
$n=7$
\begin{axiom}
radicalSolve(z^7=2)
\end{axiom}

comments

  Of course, these are correct solutions by Euler's Formula. A bit surprising that
radicalSolve invokes these for $z^7=2$ and not for $z^7=1$; when $n$ is 7, these
trignometric values are not embeddable in a tower of "solvable" extensions. That
is, these are not solutions expressible in terms of radicals (of *real* numbers)
and arithmetic alone. Put another way, the regular 7-gon is not constructible by
compass and ruler alone. From:

-  http://mathworld.wolfram.com/ConstructiblePolygon.html

-  http://mathworld.wolfram.com/TrigonometryAngles.html

A necessary and sufficient condition that a regular n-gon be constructible is
that phi(n) be a power of 2, where phi(n) is the totient function (Krízek 2001,
p. 34)::

  n =  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17 18 19 20
  phi= 1  1  2  2  4  2  6  4  6   4  10   4  12   6   8   8  16  6 18  8
  bad=                   x     x       x       x   x              x  x
  Vladimir's "not good" values are 
  n =                    7            11      13  14  15      17    19

So if you compare the constructible regular n-gons, you can see why Axiom's
results are reasonable: radicalSolve only finds solutions that are expressible
in terms of radicals and arithmetic operations. It did not find those for $n = 15$
and $17$ probably (I am guessing) because at the time of implementation, these
constructions were not known (at least to the programmer). On the other hand,
for $n = 9, 18$, the solutions are expressible in radicals only if radicals of
*complex* numbers are allowed and Axiom found those (perhaps it shouldn't?). The
expansion for $(-1)^{1/7}$ that Vladimir gave involves radicals of complex
numbers, as theory predicts.


When Axiom cannot find solutions, it is (presumably) a PROOF that the other
solutions are NOT solvable by radicals (using *real* numbers), or at least,
there is no known proof that it is solvable at the time of implementation. (That
is why I am surprised at the above result for $z^7=2$).

In other words, rather than viewing the answer for $z^7=1$ as a bug, we should
view the answers for $z^7=2$, $z^7=3$ (and may be even $z^9=1$, $z^{18}=1$) as bugs!

Still, the package should be upgraded.

-------------------

\begin{axiom}
radicalSolve(z^9=1,z)
radicalSolve(z^7=3)
radicalSolve(z^7=1.)
radicalSolve(z^6+z^5+z^4+z^3+z^2+z+1=0)
\end{axiom}

William

From BobMcElrath Mon Jan 17 22:15:05 -0600 2005
From: Bob McElrath
Date: Mon, 17 Jan 2005 22:15:05 -0600
Subject: (new)
Message-ID: <20050118041514.GA30214@mcelrath.org>
In-Reply-To: <20050117210215-0600@page.axiom-developer.org>

anonymous [mathaction@axiom-developer.org] wrote:
> When Axiom cannot find solutions, it is (presumably) a PROOF that the other
> solutions are NOT solvable by radicals (using *real* numbers), or at least,
> there is no known proof that it is solvable at the time of implementation. (That
> is why I am surprised at the above result for z^7=2).

Given Axiom's assumptions about input in this problem, why cannot I do
this:

\begin{axiom}
    z:Complex(Float)
    radicalSolve(z^7=1)
    z:Integer
    radicalSolve(z^7=1)
    z:Variable(Complex(Float))
    radicalSolve(z^7=1)
    z:Symbol(Complex(Float))
    radicalSolve(z^7=1)
\end{axiom}


...and get the appropriate answers?

Also this behind-the-scenes behavior where the answer depends on the
input type or assumptions is undesirable, and surprising to casual
users.  When algorithms must make assumptions about the type of a
Variable or Symbol, at the very least a message should be printed
indicating that the assumption was made.

An even better algorithm would print a message, then keep that
assumption for the remainder of the calculation...



From unknown Mon Jan 17 22:19:23 -0600 2005
From: 
Date: Mon, 17 Jan 2005 22:19:23 -0600
Subject: Original question
Message-ID: <20050117221923-0600@page.axiom-developer.org>

....................................................................

Obviously, all the roots of the equation $z^7 = 1$ can be expressed in
radicals, and Mathematica can easily produce the explicit expressions
in terms of radicals::

  Solve[z^7 == 1, z]

  {{z -> 1}, {z -> -(-1)^(1/7)}, {z -> (-1)^(2/7)}, {z -> -(-1)^(3/7)},
  {{z -> {z -> (-1)^(4/7)}, {z -> -(-1)^(5/7)}, {z -> (-1)^(6/7)}}

To save the space, below the only example is given::

  FunctionExpand[ComplexExpand[-(-1)^(1/7)]]
  
  (1/2)*((1/3)*((1/2)*(-1 + I*Sqrt[7]) + ((-1 + I*Sqrt[3])*((1/2)*(-1 +
  I*Sqrt[7]) + (1/2)*(-1 - I*Sqrt[7])*((1/2)*(-1 + I*Sqrt[3]) +
  (1/4)*(-1 + I*Sqrt[3])^2)))/(2*(6 + (3/4)*(-1 + I*Sqrt[3])*(-1 +
  I*Sqrt[7]) + (1/2)*(-1 - I*Sqrt[7])*(1 + (3/4)*(-1 +
  I*Sqrt[3])^2))^(1/3)) + (1/4)*(-1 + I*Sqrt[3])^2*(6 + (3/4)*(-1 +
  I*Sqrt[3])*(-1 + I*Sqrt[7]) + (1/2)*(-1 - I*Sqrt[7])*(1 + (3/4)*(-1 +
  I*Sqrt[3])^2))^(1/3)) +(1/3)*((1/2)*(1 + I*Sqrt[7]) - ((-1 +
  I*Sqrt[3])^2*((1/2)*(-1 -I*Sqrt[7]) + (1/2)*(-1 +
  I*Sqrt[7])*((1/2)*(-1 + I*Sqrt[3]) + (1/4)*(-1 + I*Sqrt[3])^2)))/(4*(6
  + (3/4)*(-1 + I*Sqrt[3])*(-1 - I*Sqrt[7]) + (1/2)*(-1 + I*Sqrt[7])*(1
  + (3/4)*(-1 + I*Sqrt[3])^2))^(1/3)) -(1/2)*(-1 + I*Sqrt[3])*(6 +
  (3/4)*(-1 + I*Sqrt[3])*(-1 - I*Sqrt[7]) + (1/2)*(-1 + I*Sqrt[7])*(1 +
  (3/4)*(-1 + I*Sqrt[3])^2))^(1/3))) + (1/2)*((1/3)*((1/2)*(-1 +
  I*Sqrt[7]) + ((-1 + I*Sqrt[3])*((1/2)*(-1 + I*Sqrt[7]) + (1/2)*(-1 -
  I*Sqrt[7])*((1/2)*(-1 + I*Sqrt[3]) + (1/4)*(-1 + I*Sqrt[3])^2)))/(2*(6
  + (3/4)*(-1 + I*Sqrt[3])*(-1 + I*Sqrt[7]) + (1/2)*(-1 - I*Sqrt[7])*(1
  + (3/4)*(-1 + I*Sqrt[3])^2))^(1/3)) +(1/4)*(-1 + I*Sqrt[3])^2*(6 +
  (3/4)*(-1 + I*Sqrt[3])*(-1 + I*Sqrt[7]) + (1/2)*(-1 - I*Sqrt[7])*(1 +
  (3/4)*(-1 + I*Sqrt[3])^2))^(1/3)) + (1/3)*((1/2)*(-1 - I*Sqrt[7])
  +((-1 + I*Sqrt[3])^2*((1/2)*(-1 - I*Sqrt[7]) + (1/2)*(-1 +
  I*Sqrt[7])*((1/2)*(-1 + I*Sqrt[3]) + (1/4)*(-1 + I*Sqrt[3])^2)))/(4*(6
  + (3/4)*(-1 + I*Sqrt[3])*(-1 - I*Sqrt[7]) + (1/2)*(-1 + I*Sqrt[7])*(1
  + (3/4)*(-1 + I*Sqrt[3])^2))^(1/3)) +(1/2)*(-1 + I*Sqrt[3])*(6 +
  (3/4)*(-1 + I*Sqrt[3])*(-1 - I*Sqrt[7]) + (1/2)*(-1 + I*Sqrt[7])*(1 +
  (3/4)*(-1 + I*Sqrt[3])^2))^(1/3)))

According to the AXIOM Book--

  Use radicalSolve if you want your solutions expressed in
  terms of radicals.
 
However, already for z^7 = 1 this is not so,

\begin{axiom} 
radicalSolve(z^7=1, z)
\end{axiom}

and the problem exists for 11, 13, 14, 15, 17, 19 etc

\begin{axiom}
for i in 1..20 repeat print([i,#radicalSolve(z^i=1,z)])
\end{axiom}

::

    [1,1]
    [2,2]
    [3,3]
    [4,4]
    [5,5]
    [6,6]
    [7,1]   <-- not good
    [8,8]
    [9,9]
    [10,10]
    [11,1]  <-- not good
    [12,12]
    [13,1]  <-- not good
    [14,2]  <-- not good
    [15,7]  <-- not good
    [16,16]
    [17,1]  <-- not good
    [18,18]
    [19,1]  <-- not good
    [20,20]
 

Best,

Vladimir

Submitted by : (unknown) at: 2007-11-17T21:55:37-08:00 (17 years ago)
Name :
Axiom Version :
Category : Severity : Status :
Optional subject :  
Optional comment :

From
William Sit
Subject
Re: [Axiom-developer]? [Q]? radicalSolve fails to find all roots ?
Date
Mon, 17 Jan 2005 16:31:52 -0500

These are NOT bugs! But the following may be! Consider the equation LatexWiki Image for LatexWiki Image 

axiom
radicalSolve(z^7=2)
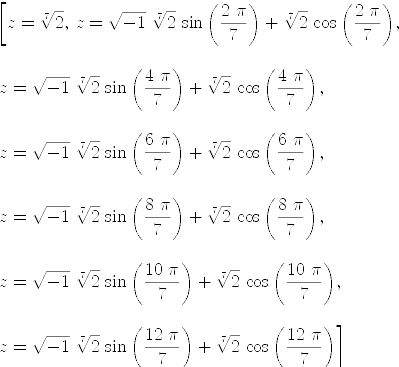LatexWiki Image(1)
Type: List Equation Expression Integer

comments

Of course, these are correct solutions by Euler's Formula. A bit surprising that radicalSolve invokes these for LatexWiki Image and not for LatexWiki Image; when LatexWiki Image is 7, these trignometric values are not embeddable in a tower of "solvable" extensions. That is, these are not solutions expressible in terms of radicals (of real numbers) and arithmetic alone. Put another way, the regular 7-gon is not constructible by compass and ruler alone. From:

A necessary and sufficient condition that a regular n-gon be constructible is that phi(n) be a power of 2, where phi(n) is the totient function (Krízek 2001, p. 34): 

  n =  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17 18 19 20
  phi= 1  1  2  2  4  2  6  4  6   4  10   4  12   6   8   8  16  6 18  8
  bad=                   x     x       x       x   x              x  x
  Vladimir's "not good" values are 
  n =                    7            11      13  14  15      17    19

So if you compare the constructible regular n-gons, you can see why Axiom's results are reasonable: radicalSolve only finds solutions that are expressible in terms of radicals and arithmetic operations. It did not find those for LatexWiki Image and LatexWiki Image probably (I am guessing) because at the time of implementation, these constructions were not known (at least to the programmer). On the other hand, for LatexWiki Image, the solutions are expressible in radicals only if radicals of complex numbers are allowed and Axiom found those (perhaps it shouldn't?). The expansion for LatexWiki Image that Vladimir gave involves radicals of complex numbers, as theory predicts.

When Axiom cannot find solutions, it is (presumably) a PROOF that the other solutions are NOT solvable by radicals (using real numbers), or at least, there is no known proof that it is solvable at the time of implementation. (That is why I am surprised at the above result for LatexWiki Image).

In other words, rather than viewing the answer for LatexWiki Image as a bug, we should view the answers for LatexWiki Image, LatexWiki Image (and may be even LatexWiki Image, LatexWiki Image) as bugs!

Still, the package should be upgraded.

-------------------

axiom
radicalSolve(z^9=1,z)
LatexWiki Image(2)
Type: List Equation Expression Integer
axiom
radicalSolve(z^7=3)
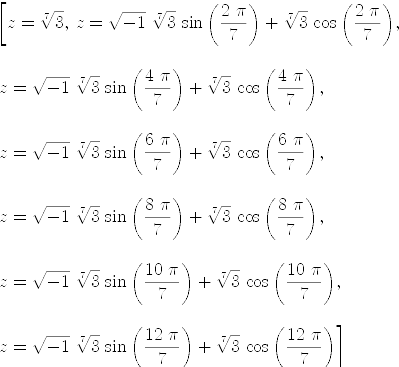LatexWiki Image(3)
Type: List Equation Expression Integer
axiom
radicalSolve(z^7=1.)
                                                     7
   WARNING (genufact): No known algorithm to factor ?  - 1.0
     , trying square-free.
LatexWiki Image(4)
Type: List Equation Expression Float
axiom
radicalSolve(z^6+z^5+z^4+z^3+z^2+z+1=0)
LatexWiki Image(5)
Type: List Equation Expression Integer

William

(new) --Bob McElrath?, Mon, 17 Jan 2005 22:15:05 -0600 reply
anonymous [mathaction@axiom-developer.org]? wrote:
When Axiom cannot find solutions, it is (presumably) a PROOF that the other solutions are NOT solvable by radicals (using real numbers), or at least, there is no known proof that it is solvable at the time of implementation. (That is why I am surprised at the above result for z^7=2).

Given Axiom's assumptions about input in this problem, why cannot I do this:

axiom
z:Complex(Float)
    radicalSolve(z^7=1)
    z:Integer
    radicalSolve(z^7=1)
    z:Variable(Complex(Float))
    radicalSolve(z^7=1)
    z:Symbol(Complex(Float))
    radicalSolve(z^7=1)
   Category, domain or package constructor ComplexFloat is not 
      available.

...and get the appropriate answers?

Also this behind-the-scenes behavior where the answer depends on the input type or assumptions is undesirable, and surprising to casual users. When algorithms must make assumptions about the type of a Variable or Symbol, at the very least a message should be printed indicating that the assumption was made.

An even better algorithm would print a message, then keep that assumption for the remainder of the calculation...

Original question
Mon, 17 Jan 2005 22:19:23 -0600 reply
....................................................................

Obviously, all the roots of the equation LatexWiki Image can be expressed in radicals, and Mathematica can easily produce the explicit expressions in terms of radicals: 

  Solve[z^7 == 1, z]

  {{z -> 1}, {z -> -(-1)^(1/7)}, {z -> (-1)^(2/7)}, {z -> -(-1)^(3/7)},
  {{z -> {z -> (-1)^(4/7)}, {z -> -(-1)^(5/7)}, {z -> (-1)^(6/7)}}

To save the space, below the only example is given: 

  FunctionExpand[ComplexExpand[-(-1)^(1/7)]]

  (1/2)*((1/3)*((1/2)*(-1 + I*Sqrt[7]) + ((-1 + I*Sqrt[3])*((1/2)*(-1 +
  I*Sqrt[7]) + (1/2)*(-1 - I*Sqrt[7])*((1/2)*(-1 + I*Sqrt[3]) +
  (1/4)*(-1 + I*Sqrt[3])^2)))/(2*(6 + (3/4)*(-1 + I*Sqrt[3])*(-1 +
  I*Sqrt[7]) + (1/2)*(-1 - I*Sqrt[7])*(1 + (3/4)*(-1 +
  I*Sqrt[3])^2))^(1/3)) + (1/4)*(-1 + I*Sqrt[3])^2*(6 + (3/4)*(-1 +
  I*Sqrt[3])*(-1 + I*Sqrt[7]) + (1/2)*(-1 - I*Sqrt[7])*(1 + (3/4)*(-1 +
  I*Sqrt[3])^2))^(1/3)) +(1/3)*((1/2)*(1 + I*Sqrt[7]) - ((-1 +
  I*Sqrt[3])^2*((1/2)*(-1 -I*Sqrt[7]) + (1/2)*(-1 +
  I*Sqrt[7])*((1/2)*(-1 + I*Sqrt[3]) + (1/4)*(-1 + I*Sqrt[3])^2)))/(4*(6
  + (3/4)*(-1 + I*Sqrt[3])*(-1 - I*Sqrt[7]) + (1/2)*(-1 + I*Sqrt[7])*(1
  + (3/4)*(-1 + I*Sqrt[3])^2))^(1/3)) -(1/2)*(-1 + I*Sqrt[3])*(6 +
  (3/4)*(-1 + I*Sqrt[3])*(-1 - I*Sqrt[7]) + (1/2)*(-1 + I*Sqrt[7])*(1 +
  (3/4)*(-1 + I*Sqrt[3])^2))^(1/3))) + (1/2)*((1/3)*((1/2)*(-1 +
  I*Sqrt[7]) + ((-1 + I*Sqrt[3])*((1/2)*(-1 + I*Sqrt[7]) + (1/2)*(-1 -
  I*Sqrt[7])*((1/2)*(-1 + I*Sqrt[3]) + (1/4)*(-1 + I*Sqrt[3])^2)))/(2*(6
  + (3/4)*(-1 + I*Sqrt[3])*(-1 + I*Sqrt[7]) + (1/2)*(-1 - I*Sqrt[7])*(1
  + (3/4)*(-1 + I*Sqrt[3])^2))^(1/3)) +(1/4)*(-1 + I*Sqrt[3])^2*(6 +
  (3/4)*(-1 + I*Sqrt[3])*(-1 + I*Sqrt[7]) + (1/2)*(-1 - I*Sqrt[7])*(1 +
  (3/4)*(-1 + I*Sqrt[3])^2))^(1/3)) + (1/3)*((1/2)*(-1 - I*Sqrt[7])
  +((-1 + I*Sqrt[3])^2*((1/2)*(-1 - I*Sqrt[7]) + (1/2)*(-1 +
  I*Sqrt[7])*((1/2)*(-1 + I*Sqrt[3]) + (1/4)*(-1 + I*Sqrt[3])^2)))/(4*(6
  + (3/4)*(-1 + I*Sqrt[3])*(-1 - I*Sqrt[7]) + (1/2)*(-1 + I*Sqrt[7])*(1
  + (3/4)*(-1 + I*Sqrt[3])^2))^(1/3)) +(1/2)*(-1 + I*Sqrt[3])*(6 +
  (3/4)*(-1 + I*Sqrt[3])*(-1 - I*Sqrt[7]) + (1/2)*(-1 + I*Sqrt[7])*(1 +
  (3/4)*(-1 + I*Sqrt[3])^2))^(1/3)))

According to the AXIOM Book--

Use radicalSolve if you want your solutions expressed in terms of radicals.

However, already for z^7 = 1 this is not so,

axiom
radicalSolve(z^7=1, z)
LatexWiki Image(6)
Type: List Equation Expression Integer

and the problem exists for 11, 13, 14, 15, 17, 19 etc

axiom
for i in 1..20 repeat print([i,#radicalSolve(z^i=1,z)])
   [1,1]
   [2,2]
   [3,3]
   [4,4]
   [5,5]
   [6,6]
   [7,1]
   [8,8]
   [9,9]
   [10,10]
   [11,1]
   [12,12]
   [13,1]
   [14,2]
   [15,7]
   [16,16]
   [17,1]
   [18,18]
   [19,1]
   [20,20]
Type: Void

    [1,1]
    [2,2]
    [3,3]
    [4,4]
    [5,5]
    [6,6]
    [7,1]   <-- not good
    [8,8]
    [9,9]
    [10,10]
    [11,1]  <-- not good
    [12,12]
    [13,1]  <-- not good
    [14,2]  <-- not good
    [15,7]  <-- not good
    [16,16]
    [17,1]  <-- not good
    [18,18]
    [19,1]  <-- not good
    [20,20]

Best,

Vladimir