MathAction numerical linear algebra

Topics

FrontPage
- FAQ
  - FriCAS Problems
    - numerical linear algebra <-- You are here.

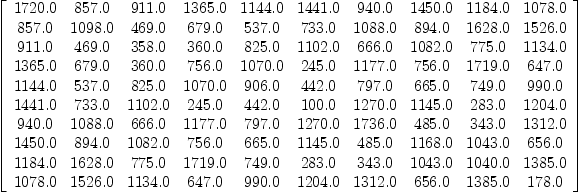
I want to get (estimates of) the eigenvalues of a 10x10 matrix of floats:

fricas

(1) -> m := matrix([[random(1000)$Integer for i in 1..10] for j in 1..10]); sm := m + transpose(m); smf:Matrix Float := sm

$\label{eq1}\left[ \begin{array}{cccccccccc} {1720.0}&{857.0}&{911.0}&{1365.0}&{1144.0}&{1441.0}&{940.0}&{1 450.0}&{1184.0}&{1078.0} \ {857.0}&{1098.0}&{469.0}&{679.0}&{537.0}&{733.0}&{1088.0}&{89 4.0}&{1628.0}&{1526.0} \ {911.0}&{469.0}&{358.0}&{360.0}&{825.0}&{1102.0}&{666.0}&{108 2.0}&{775.0}&{1134.0} \ {1365.0}&{679.0}&{360.0}&{756.0}&{1070.0}&{245.0}&{1177.0}&{7 56.0}&{1719.0}&{647.0} \ {1144.0}&{537.0}&{825.0}&{1070.0}&{906.0}&{442.0}&{797.0}&{66 5.0}&{749.0}&{990.0} \ {1441.0}&{733.0}&{1102.0}&{245.0}&{442.0}&{100.0}&{1270.0}&{1 145.0}&{283.0}&{1204.0} \ {940.0}&{1088.0}&{666.0}&{1177.0}&{797.0}&{1270.0}&{1736.0}&{4 85.0}&{343.0}&{1312.0} \ {1450.0}&{894.0}&{1082.0}&{756.0}&{665.0}&{1145.0}&{485.0}&{1 168.0}&{1043.0}&{656.0} \ {1184.0}&{1628.0}&{775.0}&{1719.0}&{749.0}&{283.0}&{343.0}&{1 043.0}&{1040.0}&{1385.0} \ {1078.0}&{1526.0}&{1134.0}&{647.0}&{990.0}&{1204.0}&{1312.0}&{6 56.0}&{1385.0}&{178.0}$

(1)

Type: Matrix(Float)

The problem is: If I now call eigenvalues(smf) on the symmetric float matrix smf Axiom 3.0 Beta (February 2005) runs for a very long time (uncomment code if you want to try it):

fricas

)set messages time on

Try this::

fricas

)set output tex off

fricas

)set output algebra on

eigen:=eigenvalues(sm)

   (2)
   [
       %B
     | 
           10          9              8                 7                    6
         %B   - 9060 %B  - 10221631 %B  + 53692462934 %B  + 32991488690592 %B
       + 
                                5                          4
         - 103347836372632698 %B  - 39496518001034749286 %B
       + 
                                   3                                2
         67792682723480658193502 %B  + 13238675729925514491568164 %B
       + 
         - 6411346841697177723823479672 %B - 777550587908816635397837762624
     ]

Type: List(Union(Fraction(Polynomial(Integer)),SuchThat?(Symbol,Polynomial(Integer))))

fricas

Time: 0.04 (OT) = 0.04 sec
solve(rhs(eigen.1),10.0^(-15))

   (3)
   [%B = - 110.9548091175_7676212, %B = - 367.9868971146_480825,
    %B = - 1238.2551231278_173671, %B = - 1395.4394073487_777468,
    %B = - 1651.8389981628_01269, %B = 9515.9502244910_992075,
    %B = 1609.8532163864_54188, %B = 1401.1491995200_013201,
    %B = 980.4992467521_7715242, %B = 317.0233477218_8936052]

Type: List(Equation(Polynomial(Float)))

fricas

Time: 0.01 sec

Thank you! This helps, but doesn't answer everything. Since interestingly:

fricas

charpol := reduce(*, [ rhs(x) - lhs(x) for x in % ])

   (4)
       10                            9                           8
     %B   - 9060.0000000000_000009 %B  - 10221630.9999999999_9 %B
   + 
                              7                            6
     5_3692462934.000000007 %B  + 3299_1488690591.999971 %B
   + 
                                5                             4
     - 10334783_6372632698.02 %B  - 3949651800_1034749284.0 %B
   + 
                                    3                                  2
     0.6779268272_3480658214 E 23 %B  + 0.1323867572_9925514525 E 26 %B
   + 
     - 0.6411346841_6971777309 E 28 %B - 0.7775505879_0881663822 E 30

Type: Polynomial(Float)

fricas

Time: 0 sec

we cannot recover the characteristic polynomial from this solution.

To recover characteristic polynomial one needs good precision, which means very small second argument to solve.

To have use of precise solution we also need to increase precision of other floating point computations using digits. Unfortunately, this leads to ugly display, so we only show final result:

fricas

digits(40)

   (5)  20

Type: PositiveInteger?

fricas

Time: 0 sec
ev:= solve(rhs(eigen.1),1.0*10^(-35));

Type: List(Equation(Polynomial(Float)))

fricas

Time: 0 sec
cp:= reduce(*, [rhs(x)-lhs(x) for x in ev])

   (7)
       10            9                                                  8
     %B   - 9060.0 %B  - 10221630.9999999999_9999999999_9999999999_98 %B
   + 
                                                    7
     5_3692462933.9999999999_9999999999_999999996 %B
   + 
                                                    6
     3299_1488690591.9999999999_9999999999_999998 %B
   + 
                                                      5
     - 10334783_6372632697.9999999999_9999999999_97 %B
   + 
                                                     4
     - 3949651800_1034749286.0000000000_0000000017 %B
   + 
                                                    3
     677_9268272348_0658193501.9999999999_9999964 %B
   + 
                                                   2
     132386_7572992551_4491568164.0000000000_002 %B
   + 
     - 64113468_4169717772_3823479671.9999999999_53 %B
   + 
     - 7775505879_0881663539_7837762624.0000000043

Type: Polynomial(Float)

fricas

Time: 0 sec
rhs(eigen.1) - cp

   (8)
                   8               7               6               5
     - 0.2 E -31 %B  + 0.4 E -28 %B  + 0.2 E -25 %B  - 0.3 E -21 %B
   + 
                 4               3               2
     0.2 E -18 %B  + 0.4 E -15 %B  - 0.2 E -12 %B  - 0.5 E -10 %B + 0.4 E -8

Type: Polynomial(Float)

fricas

Time: 0 sec

fricas

)set output algebra off

fricas

)set output tex on

For matrices of expressions one has to explicitly specify package:

fricas

A:=matrix[[cos(x),-sin(x)],[sin(x),cos(x)]]

$\label{eq2}\left[ \begin{array}{cc} {\cos \left({x}\right)}& -{\sin \left({x}\right)} \ {\sin \left({x}\right)}&{\cos \left({x}\right)}$

(2)

Type: Matrix(Expression(Integer))

fricas

Time: 0.01 (OT) = 0.01 sec
A(1,1)

$\label{eq3}\cos \left({x}\right)$

(3)

Type: Expression(Integer)

fricas

Time: 0 sec
eigen:=eigenvalues(A)$InnerEigenPackage(EXPR(INT))

$\label{eq4}\left[{{{?}^{2}}-{2 \ {\cos \left({x}\right)}\ ?}+{{\sin \left({x}\right)}^{2}}+{{\cos \left({x}\right)}^{2}}}\right]$

(4)

Type: List(Union(Expression(Integer),SparseUnivariatePolynomial?(Expression(Integer))))

fricas

Time: 0 sec

Unfortunatly, result is unsimplified, siplification is separate, for example

fricas

map(simplify, eigen(1))

$\label{eq5}{{?}^{2}}-{2 \ {\cos \left({x}\right)}\ ?}+ 1$

(5)

Type: SparseUnivariatePolynomial?(Expression(Integer))

fricas

Time: 0 sec

test --unknown, Fri, 24 Jun 2005 08:05:16 -0500 reply

fricas

A:=matrix[[cos(x)-L,-sin(x)],[sin(x),cos(x)-L]]

$\label{eq6}\left[ \begin{array}{cc} {{\cos \left({x}\right)}- L}& -{\sin \left({x}\right)} \ {\sin \left({x}\right)}&{{\cos \left({x}\right)}- L}$

(6)

Type: Matrix(Expression(Integer))

fricas

Time: 0 sec
A(1,1)*A(2,2)

$\label{eq7}{{\cos \left({x}\right)}^{2}}-{2 \ L \ {\cos \left({x}\right)}}+{{L}^{2}}$

(7)

Type: Expression(Integer)

fricas

Time: 0 sec
A(2,1)*A(1,2)

$\label{eq8}-{{\sin \left({x}\right)}^{2}}$

(8)

Type: Expression(Integer)

fricas

Time: 0 sec
A(1,1)*A(2,2)-A(2,1)*A(1,2)

$\label{eq9}{{\sin \left({x}\right)}^{2}}+{{\cos \left({x}\right)}^{2}}-{2 \ L \ {\cos \left({x}\right)}}+{{L}^{2}}$

(9)

Type: Expression(Integer)

fricas

Time: 0 sec
B := solve(A(1,1)*A(2,2)-A(2,1)*A(1,2)=0,L)

$\label{eq10}\left[{L ={{{\sqrt{- 1}}\ {\sin \left({x}\right)}}+{\cos \left({x}\right)}}}, \:{L ={-{{\sqrt{- 1}}\ {\sin \left({x}\right)}}+{\cos \left({x}\right)}}}\right]$

(10)

Type: List(Equation(Expression(Integer)))

fricas

Time: 0 sec
B(1)

$\label{eq11}L ={{{\sqrt{- 1}}\ {\sin \left({x}\right)}}+{\cos \left({x}\right)}}$

(11)

Type: Equation(Expression(Integer))

fricas

Time: 0 sec

test --unknown, Fri, 24 Jun 2005 08:16:56 -0500 reply

fricas

solve(x^2 - 2,x)

$\label{eq12}\left[{{{{x}^{2}}- 2}= 0}\right]$

(12)

Type: List(Equation(Fraction(Polynomial(Integer))))

fricas

Time: 0 sec
sqrt(2)

$\label{eq13}\sqrt{2}$

(13)

Type: AlgebraicNumber?

fricas

Time: 0 sec
solve(x^2=4,x)

$\label{eq14}\left[{x = 2}, \:{x = - 2}\right]$

(14)

Type: List(Equation(Fraction(Polynomial(Integer))))

fricas

Time: 0 sec

... --unknown, Fri, 07 Oct 2005 16:14:35 -0500 reply

fricas

P:=matrix[[a, b], [1.0 - a, 1.0 - b]]

$\label{eq15}\left[ \begin{array}{cc} a & b \ {-{{1.0}\ a}+{1.0}}&{-{{1.0}\ b}+{1.0}}$

(15)

Type: Matrix(Polynomial(Float))

fricas

Time: 0 sec
eigenvectors(P)

   There are 1 exposed and 1 unexposed library operations named 
      eigenvectors having 1 argument(s) but none was determined to be 
      applicable. Use HyperDoc Browse, or issue
                          )display op eigenvectors
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named 
      eigenvectors with argument type(s) 
                          Matrix(Polynomial(Float))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Subject: Be Bold !!

	( 15 subscribers )