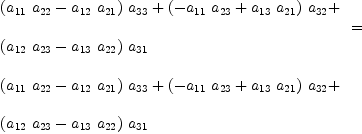LUDecomposition (LUD) LU decomposition for ordinary matrices. fricas (1) -> )expose LUDecomposition
Type: Matrix(Polynomial(Integer))
fricas diagProduct(x) == reduce(*, Type: Void
fricas B:=LUDecomp A; Type: Record(LU: Matrix(Fraction(Polynomial(Integer))),
fricas B.LU
Type: Matrix(Fraction(Polynomial(Integer)))
fricas B.Perm
Type: Vector(Integer)
fricas B.Pivots
Type: List(Fraction(Polynomial(Integer)))
fricas diagProduct(B.LU)=determinant A fricas Compiling function diagProduct with type Matrix(Fraction(Polynomial(
Integer))) -> Fraction(Polynomial(Integer))
Type: Equation(Fraction(Polynomial(Integer)))
fricas %::Boolean
Type: Boolean
|
|
|
|
last edited 12 years ago by page |
![\label{eq1}\left[
\begin{array}{ccc}
{a_{11}}&{a_{21}}&{a_{31}}
\
{a_{12}}&{a_{22}}&{a_{32}}
\
{a_{13}}&{a_{23}}&{a_{33}}](images/69904982121776732-16.0px.png "\label{eq1}\left[
\begin{array}{ccc}
{a_{11}}&{a_{21}}&{a_{31}}
\
{a_{12}}&{a_{22}}&{a_{32}}
\
{a_{13}}&{a_{23}}&{a_{33}}")
![\label{eq2}\left[
\begin{array}{ccc}
{a_{11}}&{a_{21}}&{a_{31}}
\
{\frac{a_{12}}{a_{11}}}&{\frac{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}{a_{11}}}&{\frac{{{a_{11}}\ {a_{32}}}-{{a_{12}}\ {a_{3
1}}}}{a_{11}}}
\
{\frac{a_{13}}{a_{11}}}&{\frac{{{a_{11}}\ {a_{23}}}-{{a_{13}}\ {a_{21}}}}{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}}&{\frac{{{\left({{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}\right)}\ {a_{33}}}+{{\left(-{{a_{11}}\ {a_{23}}}+{{a_{13}}\ {a_{21}}}\right)}\ {a_{32}}}+{{\left({{a_{12}}\ {a_{23}}}-{{a_{13}}\ {a_{22}}}\right)}\ {a_{31}}}}{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}}](images/7493517685198342062-16.0px.png "\label{eq2}\left[
\begin{array}{ccc}
{a_{11}}&{a_{21}}&{a_{31}}
\
{\frac{a_{12}}{a_{11}}}&{\frac{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}{a_{11}}}&{\frac{{{a_{11}}\ {a_{32}}}-{{a_{12}}\ {a_{3
1}}}}{a_{11}}}
\
{\frac{a_{13}}{a_{11}}}&{\frac{{{a_{11}}\ {a_{23}}}-{{a_{13}}\ {a_{21}}}}{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}}&{\frac{{{\left({{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}\right)}\ {a_{33}}}+{{\left(-{{a_{11}}\ {a_{23}}}+{{a_{13}}\ {a_{21}}}\right)}\ {a_{32}}}+{{\left({{a_{12}}\ {a_{23}}}-{{a_{13}}\ {a_{22}}}\right)}\ {a_{31}}}}{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}}")
![\label{eq3}\left[ 1, \: 2, \: 3 \right]](images/5939555326889798646-16.0px.png "\label{eq3}\left[ 1, \: 2, \: 3 \right]")
![\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{\frac{{{\left({{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}\right)}\ {a_{33}}}+{{\left(-{{a_{11}}\ {a_{23}}}+{{a_{13}}\ {a_{21}}}\right)}\ {a_{32}}}+{{\left({{a_{12}}\ {a_{23}}}-{{a_{13}}\ {a_{22}}}\right)}\ {a_{31}}}}{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}}, \right.
\
\
\displaystyle
\left.\:{\frac{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}{a_{1
1}}}, \:{a_{11}}\right]](images/6472554339669236970-16.0px.png "\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{\frac{{{\left({{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}\right)}\ {a_{33}}}+{{\left(-{{a_{11}}\ {a_{23}}}+{{a_{13}}\ {a_{21}}}\right)}\ {a_{32}}}+{{\left({{a_{12}}\ {a_{23}}}-{{a_{13}}\ {a_{22}}}\right)}\ {a_{31}}}}{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}}, \right.
\
\
\displaystyle
\left.\:{\frac{{{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}}{a_{1
1}}}, \:{a_{11}}\right]")
![\label{eq5}\begin{array}{@{}l}
\displaystyle
{
\begin{array}{@{}l}
\displaystyle
{{\left({{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}\right)}\ {a_{33}}}+{{\left(-{{a_{11}}\ {a_{23}}}+{{a_{13}}\ {a_{21}}}\right)}\ {a_{32}}}+
\
\
\displaystyle
{{\left({{a_{12}}\ {a_{23}}}-{{a_{13}}\ {a_{22}}}\right)}\ {a_{31}}}](images/9056350525950241280-16.0px.png "\label{eq5}\begin{array}{@{}l}
\displaystyle
{
\begin{array}{@{}l}
\displaystyle
{{\left({{a_{11}}\ {a_{22}}}-{{a_{12}}\ {a_{21}}}\right)}\ {a_{33}}}+{{\left(-{{a_{11}}\ {a_{23}}}+{{a_{13}}\ {a_{21}}}\right)}\ {a_{32}}}+
\
\
\displaystyle
{{\left({{a_{12}}\ {a_{23}}}-{{a_{13}}\ {a_{22}}}\right)}\ {a_{31}}}")
