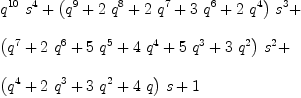MathAction #339 interpreter gives up in loop

Topics

FrontPage
- IssueTracker
  - #339 interpreter gives up in loop <-- You are here.

The following is a very surprising for a novice, and a bit surprising for me:

fricas

(1) -> c 0==1; c 1==1; c n==c(n-1)+s*(reduce(+,[q^k*c(k)*c(n-1-k) for k in 1..n-1]));

Type: Void

fricas

c 5

   Internal Error
   The function * with signature (%, Integer) -> % is missing from 
      domain Fraction(Polynomial (Integer))

Note that the type of c 5 is FRAC POLY INT. This is, because Axiom is not smart enough to realize inside the loop that 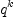is a polynomial if 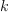is nonnegative. The following is more surprising, though:

fricas

coefficient(univariate(c(5),s),3)

   >> System error:
   The function BOOT::|*1;c;1;initial| is undefined.

Axiom manages - after a lot of trying- to coerce univariate(c(5),s) to a SUP FRAC POLY INT. Wow.

fricas

[coefficient(univariate(c(n),s),1) for n in 0..4]

   >> System error:
   The function BOOT::|*1;c;1;initial| is undefined.

But why does it give up here?

Martin

univariate applied to rational function produces rational function. Given actual value Axiom/FriCAS can see that rational function is a polynomial and retract it. But in a loop FriCAS has only expression producing rational functions and can not predict that the result will be a polynomial.

fricas

Zq:=SUP(INT)

$\label{eq1}\hbox{\axiomType{SparseUnivariatePolynomial}\ } \left({\hbox{\axiomType{Integer}\ }}\right)$

(1)

Type: Type

fricas

q:Zq := monomial(1,1)

   Compiled code for c has been cleared.

$\label{eq2}?$

(2)

Type: SparseUnivariatePolynomial?(Integer)

fricas

Zqs:=SUP(Zq)

$\label{eq3}\hbox{\axiomType{SparseUnivariatePolynomial}\ } \left({\hbox{\axiomType{SparseUnivariatePolynomial}\ } \left({\hbox{\axiomType{Integer}\ }}\right)}\right)$

(3)

Type: Type

fricas

s:Zqs := monomial(1$Zq,1)

$\label{eq4}?$

(4)

Type: SparseUnivariatePolynomial?(SparseUnivariatePolynomial?(Integer))

fricas

macro mac(n) == c(n-1) + s*(reduce(+,[q^k*c(k)*c(n-1-k) for k in 1..n-1]))

Type: Void

fricas

c(n: Integer): Zqs == (n=0 or n=1 => 1; mac n)

   Function declaration c : Integer -> SparseUnivariatePolynomial(
      SparseUnivariatePolynomial(Integer)) has been added to workspace.
   1 old definition(s) deleted for function or rule c

Type: Void

fricas

c 0

fricas

Compiling function c with type Integer -> SparseUnivariatePolynomial
      (SparseUnivariatePolynomial(Integer))

$\label{eq5}1$

(5)

Type: SparseUnivariatePolynomial?(SparseUnivariatePolynomial?(Integer))

fricas

c 1

$\label{eq6}1$

(6)

Type: SparseUnivariatePolynomial?(SparseUnivariatePolynomial?(Integer))

fricas

c 2

$\label{eq7}{{?}^{2}}+ 1$

(7)

Type: SparseUnivariatePolynomial?(SparseUnivariatePolynomial?(Integer))

fricas

mac 2

$\label{eq8}{? \ ?}+ 1$

(8)

Type: SparseUnivariatePolynomial?(SparseUnivariatePolynomial?(Integer))

I don't know but the output of c(2) is wrong. I would have expected "? ? + 1" in accordance to mac(2). So the typed form of you example doesn't work. And the output looks ugly anyway. :-(

Ralf

No, Axiom is smart enough :-) --greg, Thu, 22 Feb 2007 11:08:42 -0600 reply

In your function you are using the - operation for the upper bound, it is not defined for NNI or PI. Axiom is smart enough to detect the types of the step and the bounds. Because of that it is assumed that the result of (n-1) is an Integer.

Here I even don't define the type of the function:

fricas

)clear all

   All user variables and function definitions have been cleared.
c 0==1; c 1==1; c n==c(n-1)+s*(reduce(+,[q^k*c(k)*c(n-1-k) for k in 1..(n-1)::NNI]));

Type: Void

fricas

[coefficient(univariate(c(n),s),1) for n in 0..4]

fricas

Compiling function c with type Integer -> Polynomial(Integer)

fricas

Compiling function G36 with type Integer -> Boolean

$\label{eq9}\left[ 0, \: 0, \: q , \:{{{q}^{2}}+{2 \ q}}, \:{{{q}^{3}}+{2 \ {{q}^{2}}}+{3 \ q}}\right]$

(9)

Type: List(Polynomial(Integer))

I don't know why it gives up in your exemple though.

Greg

Subject: (replying) Be Bold !!

	( 15 subscribers )